Вопрос 34

классификация измерения в геодезии рассматриваются с двух точек зрения: количественной и качественной, выражающей числовое знаечние измеренной величины, и качественной – характер её точность

Результат любых измерений неизбежно содержит погрешность. Если Х- точное значение физической величины, а l- результат измерений этой величины, то случайнай погрешность Δ результата измерений определится формулой Δ=l-X.

Грубыми погрешностями считаются погрешности, величины которых превышают некоторый предел, установленный для данных условий измерений. Грубые погрешности возникают из за невнимательности лица, выполняющего измерения, или в следствии неисправности прибора.

Систематической погрешностью наз. составляющую погрешности измерений, остающуюся постоянной или закономерно изменяющуюся при повторных измерениях одной и той же величины.

Случайная погрешность измерений- составляющая погрешности измерений, которая изменяется случайным образом при повторных измерениях одной и той же величины.

Факторы, влияющие на результат измерений:

1)объект измерений(изменение величины объекта)

2)личные погрешности наблюдателя

3)точностные показатели прибора

4) метод измерений

5)непрерывное изменение внешних условий

Измерения, выполненные в одинаковых условиях,наз. равноточными.

Св-ва случайных погрешностей:

1)свойство симметрии относительно нуля:положительные и отрицательные погрешности, равные по абсолютной величине, равновероятны, т.е. их возникновение равновозможно.

2)свойство компенсации: сумма случайных погрешностей, полученных в результате равноточных измерений, деленная на их число, при неограниченном увеличении последнего стремится к нулю.

3)свойство рассеивания: для рядаслучайных погрешностей, полученных в результате равноточных измерений, сумма квадратов, деленная на их число, при неограниченном увеличении последнего стремится к некоторому пределу δ*δ, величина которого зависит от условий измерений.

4)свойство ограниченности: случайная погрешность по абсолютной величине не может превзойти некоторого предела Δпред, наз. предельной погрешностью.

5)свойство пропорциональности: для любых условий измерений отношение предельной погрешности к стандарту сохраняет свою величину.

6)свойство плотности: чем больше по абсолютной величине значение случайной погрешности измерений, тем оно реже встречается и, наоборот, чес меньше по модулю случайная погрешность, тем чаще она возникает.

Вопрос 35

Равноточные измерения - ряд измерений физической величины, выполненных одинаковыми по точности средствами измерений в одних и тех же условиях. Один из основных принципов геодезии требует любое измерение выполнять с контролем. В частности, любая величина (длина, угол) измеряется не один раз, а многократно. В этой связи возникает за­дача получения наиболее достоверного значения из многих изме­рений одной и той же величины.

Принцип арифметической средины. Пусть в результате равноточных измерений величины / получены значе­ния 1_Ъ /₂, ..., /„; требуется определить значение X величины /, которое будет наиболее достоверным.

Найдем отклонения б; измеренных значений l_t от искомого зна­чения X, т. е. Образуем сумму этих отклонений и разделим ее на число слага­емых

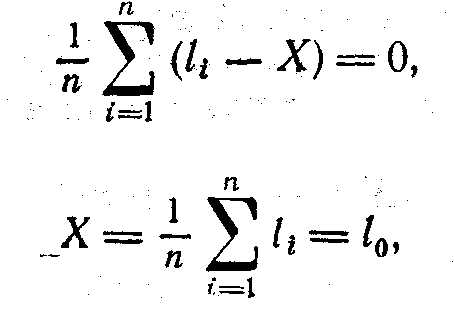Поступая обычным порядком, приравниваем нулю производную от G по X, т. е. Приведенный анализ подтверждает вывод о целесообразности принятия за достоверное значение величины / среднего арифмети­ческого из всех значений, полученных в результате измерений. Для оценки точности арифметической средины пользуются формулойСледовательно, среднее арифметическое значение /₀ имеет сред-еюю квадратическую погрешность М, которая в \fn раз меньше, эдм средняя квадратическая погрешность т каждого отдельного из­мерения.