9º Производственная функция.

В дальнейшем будем рассматривать модели, в которых учитывают либо конкретный продукт, либо ВНД. Эти величины возникают в результате взаимодействия трех факторов производства: рабочей силы (L), капитала (K), земли (N). Сказанное позволяет считать, что существует функциональная зависимость, устанавливающая величину выпуска продукта при том или ином объёме этих факторов:

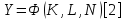
Здесь и ниже Y – объём продукта (в зависимости от рассматриваемой модели ВНД или национальный доход). Функция трех переменных [2] называется производственной функцией. В тех моделях, которые мы будем рассматривать, земля считается постоянным, неизменным фактором. Поэтому производственная функция (ПФ) рассматривается как функция лишь двух аргументов K и L:

Производная функция (ПФ) отражает технологические возможности экономики. Поскольку без капитала и рабочей силы выпуск продукта невозможен, то F(0,0)=0. Попутно заметим, что не обязательно F(0, L)=0 или F(K,0)=0.

Иногда, чтобы выяснить влияние на выпуск именно рабочей силы, считают, что капитал не изменяется: . В этом случае производственная функция будет зависеть только от L:

Подобным образом, если зафиксировать число занятых, то получим следующую формулу:

Понятно, что Y, Y^* – неубывающие функции. В дальнейшем будем считать, что эти функции возрастают, непрерывны, и, кроме того, дифференцируемы в любой внутренней точке их области определения (все точки, кроме 0). В силу закона убывающей доходности (см. п.5 конспекта семинарских занятий) они должны быть вогнутыми. Убедимся в этом, рассмотрев функцию Y(L). Для Y*(K) используются аналогичные рассуждения.

Доказательство. Пусть , где n – некоторое число. Согласно закону убывающей доходности,

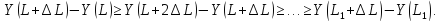
Отсюда, в частности, следует, что

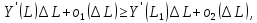
Что эквивалентно или

При достаточно малых ∆L (или при достаточно больших n) величина будет сколь угодно малой. Но тогда из последнего неравенства получаем, что . Это означает, что Y’(L), L > 0 – невозрастающая функция. Следовательно, Y(L) – вогнутая функция. □

Более того, существует такое , что в области эта функция будет строго вогнутой. Чтобы убедиться в этом, достаточно показать, что 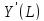является убывающей для достаточно больших значений L.

Доказательство. Предположим противное. Тогда найдётся такой отрезок , где L^* - сколь угодно большое число, что 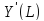– константа, где 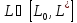. Тогда Y(L) будет линейной, и, следовательно,

С другой стороны, согласно закону убывающей доходности для достаточно больших значений L и любых ∆L > 0 должно иметь место строгое неравенство:

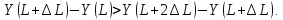
Полученное противоречие доказывает сделанное утверждение. □

Возможные графики функции Y(L), L ≥ 0 изображены на рисунке 3:

Y Y

L 0 L

Замечание: Функции не обязаны быть строго вогнутыми для достаточно больших значений аргумента, если они не являются возрастающими. Так, например, функция, изображенная на рисунке 4, соответствует закону убывающей доходности:

Y

0 L