
- •Глава 1. Элементы макроэкономической теории.
- •§1. Основные макроэкономические понятия.
- •1º Макротеория и микротеория. Агрегирование.
- •2º Факторы производства.
- •3º Износ. Амортизация и инвестиции.
- •4º Измерение объёма национального производства и национального дохода.
- •5º Сбережения и норма процента. Дисконтирование.
- •6º Ценные бумаги.
- •7º Денежная масса, номинальная и реальная заработные платы.
- •8º Международная торговля и системы валютных курсов.
- •9º Производственная функция.
- •10º Список основных макроэкономических переменных.
- •Глава 2. Классическая теория.
- •1º Макроэкономические теории.
- •2º Рынок труда.
- •3º Рынок капитала (рынок сбережений и инвестиций).
- •4º Денежный рынок.
- •5º Краткий обзор классической теории.
- •6º Сравнительная статика.
- •7º Критика классической теории.
- •Глава 2. Теория Кейнса.
- •§1 Склонность к потреблению.
- •§2 Спекулятивный спрос на деньги
- •§3 Рынок труда
- •§ 4 Рынок капитала (сбережения инвестиций)
- •5. Денежный рынок
- •6. Краткая формулировка модели. Определение равновесия.
- •7. Существование и единственность равновесия в модели Кейнса.
- •8. Инфляция и безработица.
- •9. Сравнительная статика. Изменение предложения денег.
- •10.Изменение производственной функции.
- •11. Изменение номинальной зарплаты
- •Глава 4. Экономический рост
- •1. Однопродуктовая макроэкономическая модель
- •2. Независимость производственного процесса от масштаба.
- •3. Модель Салоу.
- •4. Сбалансированный рост (ср)
- •5. Асимптотическое поведение траектории в модели Салоу
- •6. Оптимальная норма накопления (онн)
- •7. Была ли необходима перестройка в ссср?
- •Глава 5 Элементы теории потребительского потребления
- •1. Отношение предпочтения и функция полезности.
- •2 Неоклассическая задача потребления.
- •Глава 6. Теория фирм
- •1. Задача максимизации прибыли фирмы в условиях совершенной конкуренции
- •2. Несовершенная конкуренция. Монополия и монопсония
- •3 Конкуренция среди немногих. Олигополия и олигопсония.
4. Сбалансированный рост (ср)
Под Сбалансированным
ростом понимается такой процесс
экономического развития, при котором
основные макропоказатели растут с
постоянным темпом. Применительно к
рассмотренной модели это означает, что
с постоянным темпом должны возрастать
величины
 .
При сделанном в предыдущем параграфе
предположении число занятых
.
При сделанном в предыдущем параграфе
предположении число занятых
 будет обладать таким свойством. Обозначим
через
будет обладать таким свойством. Обозначим
через
 темпы роста первых четырех показателей
и сохраним принятое обозначение
темпы роста первых четырех показателей
и сохраним принятое обозначение
 для темпа роста рабочей силы.
для темпа роста рабочей силы.

Покажем, что
тогда темпы роста всех показателей
должны совпадать. В силу (2) и (17)
имеем
 следовательно, учитывая, что
следовательно, учитывая, что
 получаем, что
получаем, что
 .
Разделив обе части на
.
Разделив обе части на
 ,
из (13) и (17) следует
,
из (13) и (17) следует

После
дифференцирования по
 получим формулу
получим формулу

Эта формула
справедлива, когда
 ,
т.е
,
т.е
 .
Отсюда и из (18) следует, что
.
Отсюда и из (18) следует, что
 ,
что имеет место, когда
,
что имеет место, когда
 .
.
Сопоставляем
полученные соотношения с темпами роста.
Покажем, что
 ,
,
 - темп роста рабочей силы.
- темп роста рабочей силы.


Используя линейную однородность производственной функции, получаем формулу выше.
Т.к.
 ,
то
,
то
 .
.
Производственная
функция монотонно возрастает по каждому
аргументу, поэтому полученное тождество
может выполняться тогда и только тогда,
когда
 ,
т.е при
,
т.е при
 ;
Таким образом
;
Таким образом
 ,
что и требовалось доказать.
,
что и требовалось доказать.
При
СР темпы изменения основных макропоказателей
должны быть одинаковы, следовательно
при СР норма накопления
 и фондовооруженность
и фондовооруженность
 не зависят от времени. Это означает, что
траектории СР отвечает решение
дифференциального уравнения Салоу
(16), имеющего вид
не зависят от времени. Это означает, что
траектории СР отвечает решение
дифференциального уравнения Салоу
(16), имеющего вид
 .
Найдя такое решение, можно определить
основные макропеременные:
.
Найдя такое решение, можно определить
основные макропеременные:

Покажем,
что в рассматриваемой модели для
каждой фиксированной постоянной
нормы накопления существует единственная
траектория СР. Постоянное решение
дифференциального уравнения (16),
соответствующее СР, обращает левую
часть этого уравнения в 0, т.е. является
корнем следующего конечного уравнения
 конечное уравнение, называют такое
уравнение алгебраическим, если
конечное уравнение, называют такое
уравнение алгебраическим, если
 - полином.
- полином.

Покажем,
что при заданном постоянном значении
нормы накопления
 уравнение (20) имеет в области
уравнение (20) имеет в области
 (только такие значения имеют экономический
смысл) единственное решение. Для этого
исследуем свойства функции
(только такие значения имеют экономический
смысл) единственное решение. Для этого
исследуем свойства функции

Т.к.
 (см. пар. 2), то
(см. пар. 2), то
 .
В силу (10)
.
В силу (10)
 ,
следовательно в некоторой
правосторонней окрестности
,
следовательно в некоторой
правосторонней окрестности

 .
Из (9) следует
.
Из (9) следует
 ,
а значит
,
а значит
 при достаточно больших
при достаточно больших
 .
Сопоставляя полученные результаты,
приходим к тому, что в некоторой точке
.
Сопоставляя полученные результаты,
приходим к тому, что в некоторой точке
 ,
,
 обращается в 0. Т.к.
обращается в 0. Т.к.
 ,
то и
,
то и
 при
при
 ,
т.е.
,
т.е.
 строго вогнутая функция. Тогда она не
будет иметь положительных нулей, отличных
от
строго вогнутая функция. Тогда она не
будет иметь положительных нулей, отличных
от
 .
Возможный график этой функции изображен
на рис.3. При фиксированной постоянной
норме накопления
.
Возможный график этой функции изображен
на рис.3. При фиксированной постоянной
норме накопления
 уравнения (20) имеет в области
уравнения (20) имеет в области
 единственное решение, т.е. в рассматриваемой
модели существует единственная траектория
СР.
единственное решение, т.е. в рассматриваемой
модели существует единственная траектория
СР.
Замечание
Чем больше норма накопления
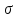 ,
тем больше фондовооруженность
,
тем больше фондовооруженность
 на траектории СР.
на траектории СР.
g

0 
рис. 3

5. Асимптотическое поведение траектории в модели Салоу
Режим
сбалансированного роста - это одна из
возможных траекторий развития
экономической системы. Если данная
модель используется для описания
реальной экономики, то любая конкретная
траектория будет определяться как
решение дифференциального уравнения
(16) с начальным условием
 - значение фондовооруженности в начальный
момент времени и не обязательно является
траекторией сбалансированного роста
(ТСР). Вместе с тем, траектории
сбалансированного роста играют важную
роль среди множества траекторий
рассматриваемых моделей: любая траектория
с постоянной нормой накопления по
прошествии достаточно большого времени
неограниченно приближается к траектории
сбалансированного роста следовательно
режим сбалансированного роста может
быть использован для расчетов экономических
показателей при достаточно больших
значениях времени, независимо от
начальных значений этих показателей.
С математической точки зрения описанное
свойство траекторий моделей выглядит
следующим образом: пусть
- значение фондовооруженности в начальный
момент времени и не обязательно является
траекторией сбалансированного роста
(ТСР). Вместе с тем, траектории
сбалансированного роста играют важную
роль среди множества траекторий
рассматриваемых моделей: любая траектория
с постоянной нормой накопления по
прошествии достаточно большого времени
неограниченно приближается к траектории
сбалансированного роста следовательно
режим сбалансированного роста может
быть использован для расчетов экономических
показателей при достаточно больших
значениях времени, независимо от
начальных значений этих показателей.
С математической точки зрения описанное
свойство траекторий моделей выглядит
следующим образом: пусть
 - фиксированное постоянное значение
нормы накопления,
- фиксированное постоянное значение
нормы накопления,
 - фондовооруженность на соответствующей
этой норме траектории сбалансированного
роста. Пусть
- фондовооруженность на соответствующей
этой норме траектории сбалансированного
роста. Пусть
 - решение дифференциального уравнения
(16) с начальным условием
- решение дифференциального уравнения
(16) с начальным условием
 ,
тогда
,
тогда
 верно:
верно:

Докажем
это утверждение. Предположим
 .
В предыдущем параграфе выяснили, что
правая часть уравнения (16) (функция
21) принимает в области
.
В предыдущем параграфе выяснили, что
правая часть уравнения (16) (функция
21) принимает в области
 положительные значения, следовательно
положительные значения, следовательно
 будет монотонно возрастать, пока её
значения принадлежат этой области
будет монотонно возрастать, пока её
значения принадлежат этой области
 .
Легко видеть, что
.
Легко видеть, что
 не покинет область
не покинет область
 ни при каких
ни при каких
 (по теореме о существовании и единственности
решения дифференциального уравнения).
Действительно, допустив противное,
будем иметь
(по теореме о существовании и единственности
решения дифференциального уравнения).
Действительно, допустив противное,
будем иметь
 при некотором
при некотором
 ,
следовательно через точку
,
следовательно через точку
 проходят по меньшей мере два решения
проходят по меньшей мере два решения
 и
и
 уравнения (16). В силу свойств
уравнения (16). В силу свойств
 правая часть уравнения удовлетворяет
условиям теоремы о существовании и
единственности решения ОДУ следует
правая часть уравнения удовлетворяет
условиям теоремы о существовании и
единственности решения ОДУ следует
 - монотонно возрастающая ограниченная
функция при
- монотонно возрастающая ограниченная
функция при
 .
Тогда по теореме Вейерштрасса
.
Тогда по теореме Вейерштрасса
 .
В силу (16)
.
В силу (16)
 .
Из существования этого предела следует,
что он равен 0. В этом можно в частности
убедиться, используя формулу конечных
приращений. Т.о.
.
Из существования этого предела следует,
что он равен 0. В этом можно в частности
убедиться, используя формулу конечных
приращений. Т.о.
 наряду с
наряду с
 является корнем (20). Как было
установлено в предыдущем параграфе,
это уравнение имеет в области
является корнем (20). Как было
установлено в предыдущем параграфе,
это уравнение имеет в области
 единственное решение, следовательно
единственное решение, следовательно
 ,
т.е. выполняется соотношение (22).
Аналогично доказывается, что если
,
т.е. выполняется соотношение (22).
Аналогично доказывается, что если
 ,
то
,
то
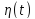 является монотонно убывающей функцией,
и имеет место соотношение (22). Если
является монотонно убывающей функцией,
и имеет место соотношение (22). Если
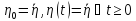 ,
то соотношение (22) опять таки верно.
Поведение траекторий уравнения (16) при
фиксированном постоянном
,
то соотношение (22) опять таки верно.
Поведение траекторий уравнения (16) при
фиксированном постоянном
 изображено на рис.4.
изображено на рис.4.

Из
полученных результатов следует, что
постоянное решение
 в уравнении (16) является устойчивым
по Ляпунову, а значит и асимптотически
устойчивым. Отметим, что доказано более
сильное свойство, чем асимптотическая
устойчивость, т.к последнее означает
сходимость
в уравнении (16) является устойчивым
по Ляпунову, а значит и асимптотически
устойчивым. Отметим, что доказано более
сильное свойство, чем асимптотическая
устойчивость, т.к последнее означает
сходимость
 тех траекторий, начальные значения
которых достаточно близки к
тех траекторий, начальные значения
которых достаточно близки к
 .
.
В
заключении рассмотрим случай, когда
производственная функция является
функцией Кома-Дугласа
 (параграф 1.9). В этом случае
(параграф 1.9). В этом случае
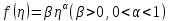 .
Тогда уравнение (16) будет иметь вид
.
Тогда уравнение (16) будет иметь вид

Непосредственной проверкой можно убедиться в том, что общее решение уравнения (23) представимо в виде:


где
 отвечает сбалансированному росту.
Значение фондовооруженности,
являющегося корнем
отвечает сбалансированному росту.
Значение фондовооруженности,
являющегося корнем
 .
.
Этот результат естественно совпадает с полученным выше результатом для произвольной линейно-однородной производственной функции.
