3. Математический маятник.

Математическим маятником называют тело небольших размеров, подвешенное на тонкой нерастяжимой нити, масса которой пренебрежимо мала по сравнению с массой тела.

Колебания маятника при больших амплитудах не являются гармоническими. Для малых колебаний математического маятника второй закон Ньютона записывается в виде

Формула Гюйгенса

4 . Физический маятник

Физическим маятником называется твердое тело, закрепленное на неподвижной горизонтальной ocи (оси подвеса), не проходящей через центр тяжести, и совершающее колебания относительно этой оси под действием силы тяжести. В отличие от математического маятника массу такого тела нельзя считать точечной.

Знак минус в правой части означает то, что сила F направлена в сторону уменьшения угла α. С учетом малости угла α

Для вывода закона движения математического и физического маятников используем основное уравнение динамики вращательного движения

Момент силы: определить в явном виде нельзя. С учетом всех величин, входящих в исходное дифференциальное уравнение колебаний физического маятника имеет вид:

Решение этого уравнения

Определим длину l математического маятника, при которой период его колебаний равен периоду колебаний физического маятника, т.е. или

Из этого соотношения определяем

Период свободных колебаний физического маятника

Если амплитуда колебаний мала, то корень в знаменателе эллиптического интеграла приближенно равен единице. Такой интеграл легко берется, и получается хорошо известная формула малых колебаний:

4. Превращение энергии в гармонических колебаний.

На примере колебаний тела на нити видим, что в положении равновесия скорость и, следовательно, кинетическая энергия тела максимальны. Если потенциальную энергию отсчитывать от положения равновесия, то она максимальна при амплитудном значении смещения, т.е. когда кинетическая энергия (скорость) равна нулю.

Т.к. мы рассматриваем свободные колебания (происходящие в отсутствие трения), то выполняется закон сохранения механической энергии: сумма кинетической и потенциальной энергий остается неизменной:

Пусть колебание происходит по закону синуса , тогда скорость меняется по закону косинуса. Запишем выражение для кинетической энергии:

Согласно закону сохранения энергии, полная энергия будет равна максимальной кинетической, т.к. в положении равновесия потенциальная равна нулю. Тогда: . Для потенциальной энергии получим:

5. Сложение гармонических колебаний.

Сложение по одной прямой.

Метод векторных диаграмм

Фигу́ры Лиссажу́ — замкнутые траектории, прочерчиваемые точкой, совершающей одновременно два гармонических колебания в двух взаимно перпендикулярных направлениях.

Затухающие механические колебания

Затухающими наз. колебания, энергия (а значит, и амплитуда) которых уменьшается с течением времени. Затухание свободных механических гармонических колебаний связано с убыванием механической энергии за счет действия сил сопротивления и трения.

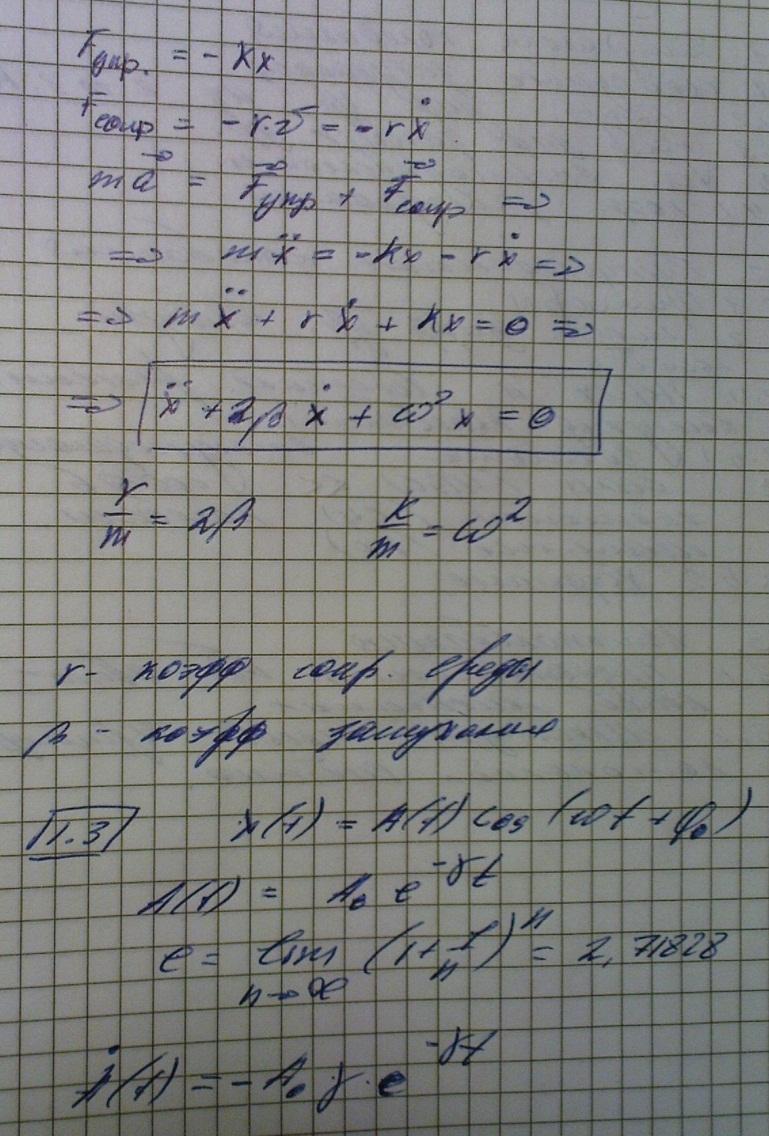
8. Характеристики затухающих колебаний

1. Коэффициент затухания .

2. Время затухания   время, за которое «амплитуда» колебаний уменьшается в e раз.

, (1.8.12)

,  ,  .

3. Декремент затухания  – число, равное отношению «амплитуд», соответствующих моментам времени, отличающимся на период.

. (1.8.14)

4. Логарифмический декремент затухания .

. (1.8.15)

Т.к. коэффициент затухания , то «амплитуда» A(t) может быть представлена в виде:

. (1.8.16)

За время затухания  система успевает совершить колебаний. Тогда, т.к. , то

. (1.8.17)

5. Добротность – безразмерная физическая величина Q, пропорциональная отношению энергии W(t) колебаний системы в некоторый момент времени t к убыли этой энергии за период колебаний, т.е. за интервал времени (t, t+T). Коэффициент пропорциональности равен 2.

. (1.8.18)

Т.к. энергия колебаний W(t) пропорциональна квадрату амплитуды колебаний: , то

,  . (1.8.19)

При малых значениях логарифмического декремента затухания () , тогда добротность системы равна

. (1.8.20)

При этом период T затухающих колебаний практически равен периоду T₀ свободных незатухающих колебаний, так что

. (1.8.21)

Чем медленнее происходит затухание свободных колебаний, тем выше добротность Q колебательной системы. Добротность системы, совершающей незатухающие гармонические колебания, равна бесконечности.