
- •Основы компьютерной арифметики и логики
- •Предисловие
- •Глава 4, подготовленная доцентом о.П. Шафеевой, посвящена вопросам разработки алгоритмических моделей выполнения арифметических операций и моделирования на пэвм спроектированных алгоритмов.
- •Основы двоичной компьютерной арифметики
- •1.1. Позиционные системы счисления
- •Десятичная позиционная система счисления
- •Двоичная позиционная система счисления
- •1.1.3. Восьмеричная позиционная система счисления
- •1.1.4. Шестнадцатеричная позиционная система счисления
- •Сложение Вычитание
- •Перевод чисел из одной позиционной системы счисления в другую
- •1.2.1. Перевод целых чисел
- •1.2.2. Перевод правильных дробей
- •1.2.3. Перевод неправильных дробей из одной системы счисления в другую
- •1.2.4. Частный случай перевода чисел из одной системы счисления в другую
- •1.2.5. Перевод чисел из одной системы счисления в другую с использованием промежуточной двоично-десятичной системы
- •1.3. Представление чисел с фиксированной запятой (точкой)
- •1.4. Представление чисел с плавающей запятой (точкой)
- •1.5. Коды двоичных чисел
- •1.5.1. Прямой код
- •1.5.2. Обратный код
- •1.5.3. Модифицированный обратный код
- •1.5.4. Дополнительный код
- •2.1.1. Алгебраическое сложение чисел в дополнительном коде
- •2.1.2. Алгебраическое сложение чисел в обратном коде
- •2.1.3. Переполнение разрядной сетки при сложении чисел
- •2.2. Сложение (вычитание) двоичных чисел с плавающей запятой
- •2.2.1. Метод ускоренного сложения двоичных чисел с запоминанием переносов
- •2.3. Умножение двоичных чисел с фиксированной запятой
- •2.4. Машинные технологии выполнения операции умножения двоичных чисел с фиксированной запятой
- •2.5. Умножение двоичных чисел с плавающей запятой
- •2.6. Методы ускоренного выполнения операции умножения двоичных чисел
- •2.6.1. Метод пропуска такта суммирования
- •2.6.2. Метод анализа сомножителей
- •2.6.3. Метод расшифровки и одновременного умножения на два разряда множителя
- •2.6.4. Метод ускоренного умножения Мак-Сорли
- •2.6.5. Метод ускоренного умножения Лемана
- •2.6.6. Метод умножения с расшифровкой пар разрядов множителя и запоминанием переносов
- •2.7. Деление двоичных чисел с фиксированной запятой
- •2.8. Деление двоичных чисел с плавающей запятой
- •3. Основы десятичной компьютерной арифметики
- •3.1. Машинное кодирование десятичных чисел
- •3.2. Выполнение арифметических операций с десятичными числами
- •3.2.1. Сложение десятичных чисел в эвм
- •3.2.2. Умножение десятичных чисел в эвм
- •3.2.3. Ускорение умножения в -кодах
- •Деление десятичных чисел в эвм
- •4.2. Моделирование алгоритма сложения двоичных чисел
- •Различные случаи ненормализованных мантисс
- •4.3. Проектирование алгоритма умножения чисел
- •4.5. Проектирование алгоритма деления чисел
- •4.7. Разработка алгоритма вычисления квадратного корня
- •Определение 1. Пусть и произвольные множества. Соответствием называется тройка множеств
- •Свойства отношений
- •Эквивалентность
- •Толерантность
- •Отношения порядка
- •Самодвойственные функции
- •Монотонные функции
- •Линейные функции
- •Функции, сохраняющие константу
- •5.2.7. Минимизация булевых функций
- •Метод Блейка
- •Метод Квайна-Мак-Класки
- •Минимизация с использованием карт Карно
- •Дана функция четырех переменных (рис. 5.13):
- •Минимизация не полностью определенных булевых функций
- •Минимизация систем булевых функций
- •5.3. Методика синтеза комбинационных схем на логических элементах
- •5.3.1. Логические элементы
- •5.3.2. Общий алгоритм построения комбинационных схем
- •5.3.3. Синтез кс в классическом базисе
- •5.3.4. Синтез кс в базисах «и-не», «или-не»
- •5.3.5. Реализация кс в базисе Жегалкина
- •5.3.6. Синтез составных кс
- •Заключение
- •Библиографический список к главам 1, 2, 3, 4
- •Библиографический список к главе 5
-
Перевод чисел из одной позиционной системы счисления в другую
1.2.1. Перевод целых чисел
Пусть
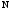 -
целое число, записанное в системе
счисления с основанием
-
целое число, записанное в системе
счисления с основанием
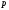 .
.
Пусть
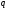 -
основание другой системы счисления,
записанное в исходной
-
основание другой системы счисления,
записанное в исходной
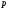 -ичной
системе счисления, причем
-ичной
системе счисления, причем
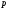
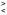
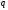 .
.
Требуется
перевести число
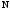 из системы счисления с основанием
из системы счисления с основанием
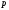 в систему счисления с основанием
в систему счисления с основанием
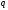
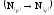 .
.
Предположим,
что изображение числа
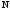 в
в
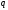 -ичной
системе счисления найдено и имеет
следующий вид:
-ичной
системе счисления найдено и имеет
следующий вид:
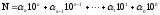 ,
(1.1)
,
(1.1)
где
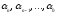 -
цифры
-
цифры
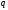 -ичной
системы, а 10 – основание этой системы,
т.е.
-ичной
системы, а 10 – основание этой системы,
т.е.
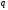 .
.
С
учетом того, что
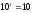 ,
а
,
а
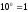 ,
заменим в правой части равенства (1.1)
числа
,
заменим в правой части равенства (1.1)
числа
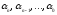 и 10 их
и 10 их
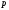 -ичными
изображениями
-ичными
изображениями
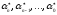 и
и
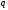 .
Тогда получим:
.
Тогда получим:
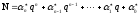 .
(1.2)
.
(1.2)
Деля
обе части равенства (1.2) на
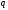 ,
имеем:
,
имеем:
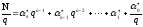 ,
(1.3)
,
(1.3)
где
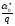 представляет собой правильную дробь,
поскольку
представляет собой правильную дробь,
поскольку
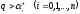 .
.
Из
равенства (1.3) видно, что при делении
числа
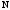 на
на
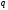 остаток равен
остаток равен
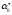 ,
а частным будет
,
а частным будет
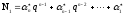 .
.
Если
теперь частное
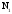 разделить на
разделить на
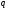 ,
то получим в остатке
,
то получим в остатке
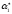 ,
а в новом частном
,
а в новом частном
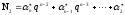 .
.
Выполняя
этот процесс деления
 раз, можно последовательно найти все
числа
раз, можно последовательно найти все
числа
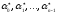 ,
причем последнее частное будет иметь
вид
,
причем последнее частное будет иметь
вид
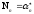 .
.
Из
сказанного вытекает следующее общее
правило перевода целых чисел

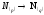 из одной позиционной системы счисления
в другую для любых оснований
из одной позиционной системы счисления
в другую для любых оснований
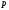 и
и
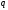 .
.
Правило
перевода. Путем
последовательного деления числа
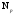 и его частных на
и его частных на
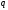 получают в виде остатков деления
получают в виде остатков деления
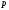 -ичные
записи
-ичные
записи
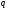 -ичных
цифр (начиная с младшей), необходимые
для изображения числа
-ичных
цифр (начиная с младшей), необходимые
для изображения числа
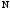 в
в
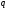 -ичной
системе счисления. Последовательное
деление производится до тех пор, пока
не получится частное, меньшее чем
-ичной
системе счисления. Последовательное
деление производится до тех пор, пока
не получится частное, меньшее чем
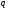 .
Это последнее частное является старшей
.
Это последнее частное является старшей
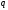 -ичной
цифрой числа
-ичной
цифрой числа
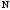 .
Деление выполняется в исходной, т.е. в
.
Деление выполняется в исходной, т.е. в
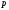 -ичной
системе счисления.
-ичной
системе счисления.
Пример.
Пусть
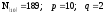 .
.
Требуется
перевести десятичное число
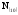 в двоичную систему счисления, т.е. найти
число
в двоичную систему счисления, т.е. найти
число
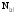 .
.
Операция Частное Остаток
189 : 2 = 94 + 1
94 : 2 = 47 + 0
47 : 2 = 23 + 1
23 : 2 = 11 + 1
11 : 2 = 5 + 1
5 : 2 = 2 + 1
2 : 2 = 1 + 0
1
Таким
образом, двоичная запись десятичного
числа
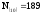 имеет следующий вид:
имеет следующий вид:
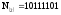 .
.
Проверка правильности перевода:
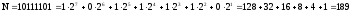 .
.
Пример.
Пусть
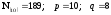 .
.
Требуется
перевести десятичное число
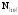 в восьмеричную систему счисления, т.е.
найти число
в восьмеричную систему счисления, т.е.
найти число
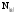 .
.
Операция Частное Остаток
189 : 8 = 23 + 5
23 : 8 = 2 + 7
2
Таким
образом, восьмеричная запись числа
 имеет следующий вид:
имеет следующий вид:
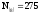 .
.
Проверка правильности перевода:
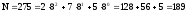 .
.
1.2.2. Перевод правильных дробей
Пусть
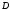 -
правильная дробь, записанная в системе
счисления с основанием
-
правильная дробь, записанная в системе
счисления с основанием
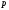 .
Пусть
.
Пусть
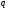 -
основание другой системы счисления,
записанное в исходной
-
основание другой системы счисления,
записанное в исходной
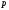 -ичной
системе счисления, причем
-ичной
системе счисления, причем
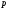
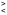
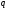 .
.
Требуется
перевести правильную дробь
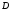 из системы счисления с основанием
из системы счисления с основанием
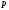 в
систему счисления с основанием
в
систему счисления с основанием
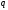 ,
т.е.
,
т.е.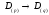 .
.
Предположим,
что изображение правильной дроби
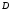 в
в
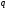 -ичной
системе счисления найдено и имеет
следующий вид:
-ичной
системе счисления найдено и имеет
следующий вид:
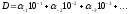 ,
(1.4)
,
(1.4)
где
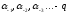 -ичные
цифры, а 10 - основание системы счисления,
т.е.
-ичные
цифры, а 10 - основание системы счисления,
т.е.
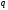 .
.
Заменяя
входящие в правую часть равенства (1.4)
числа
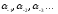 и 10 их
и 10 их
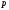 -ичными
изображениями
-ичными
изображениями
![]() и
и
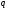 ,
получим
,
получим
![]() .
(1.5)
.
(1.5)
Умножая
обе части равенства (1.5) на
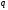 ,
имеем
,
имеем
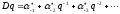 .
(1.6)
.
(1.6)
Целая
часть числа (1.6) равна
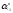 ,
а его дробной частью является
,
а его дробной частью является
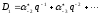 .
.
Умножая
новую дробь
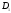 на
на
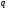 ,
получим число, целая часть которого
равна
,
получим число, целая часть которого
равна
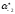 ,
а дробная часть имеет вид
,
а дробная часть имеет вид
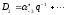 .
.
Повторяя
описанный процесс умножения нужное
количество раз, легко найти одну за
другой (в
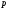 -ичной
записи)
-ичной
записи)
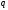 -ичные
цифры, начиная со старшей, необходимые
для изображения числа
-ичные
цифры, начиная со старшей, необходимые
для изображения числа
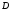 с заданной точностью.
с заданной точностью.
Из
сказанного следует общее правило
перевода правильных дробей
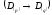 из одной позиционной системы счисления
в другую для любых оснований
из одной позиционной системы счисления
в другую для любых оснований
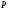 и
и
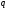 .
.
Правило
перевода. Путем
последовательного умножения числа
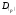 и дробных частей образующихся произведений
на
и дробных частей образующихся произведений
на
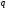 получают в виде целых частей этих
произведений
получают в виде целых частей этих
произведений
 -ичные
записи
-ичные
записи
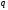 -ичных
цифр (начиная со старшей), необходимых
для изображения правильной дроби
-ичных
цифр (начиная со старшей), необходимых
для изображения правильной дроби
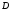 в системе счисления с основанием
в системе счисления с основанием
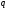 .
Умножение выполняется в исходной, т.е.
в
.
Умножение выполняется в исходной, т.е.
в
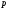 -ичной
системе счисления до тех пор, пока не
будет получена заданная точность
перевода, либо дробная часть произведения
не станет равной нулю.
-ичной
системе счисления до тех пор, пока не
будет получена заданная точность
перевода, либо дробная часть произведения
не станет равной нулю.
Пример.
Пусть
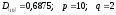 .
.
Требуется
перевести правильную десятичную дробь
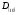 в двоичную систему счисления, т.е. найти
число
в двоичную систему счисления, т.е. найти
число
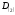 .
.
Целая Дробная
часть часть
|
0, |
х 6875 2 |
|
1, |
х 3750 2 |
|
0, |
х 7500 2 |
|
1, |
х 5000 2 |
|
1, |
0000 |
Двоичная
запись десятичной правильной дроби
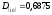 имеет следующий вид:
имеет следующий вид:
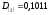 .
.
Проверка правильности перевода:
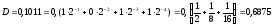 .
.
Пример.
Пусть
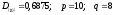 .
.
Требуется
перевести десятичную дробь
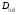 в восьмеричную систему счисления, т.е.
найти число
в восьмеричную систему счисления, т.е.
найти число
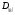 .
.
Целая Дробная
часть часть
|
0, |
х 8 |
|
5, |
х 8 |
|
4, |
0000 |
Восьмеричная
запись десятичной правильной дроби
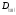 имеет
следующий вид:
имеет
следующий вид:
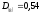 .
.
Проверка правильности перевода:
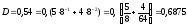 .
.
