
- •Основы компьютерной арифметики и логики
- •Предисловие
- •Глава 4, подготовленная доцентом о.П. Шафеевой, посвящена вопросам разработки алгоритмических моделей выполнения арифметических операций и моделирования на пэвм спроектированных алгоритмов.
- •Основы двоичной компьютерной арифметики
- •1.1. Позиционные системы счисления
- •Десятичная позиционная система счисления
- •Двоичная позиционная система счисления
- •1.1.3. Восьмеричная позиционная система счисления
- •1.1.4. Шестнадцатеричная позиционная система счисления
- •Сложение Вычитание
- •Перевод чисел из одной позиционной системы счисления в другую
- •1.2.1. Перевод целых чисел
- •1.2.2. Перевод правильных дробей
- •1.2.3. Перевод неправильных дробей из одной системы счисления в другую
- •1.2.4. Частный случай перевода чисел из одной системы счисления в другую
- •1.2.5. Перевод чисел из одной системы счисления в другую с использованием промежуточной двоично-десятичной системы
- •1.3. Представление чисел с фиксированной запятой (точкой)
- •1.4. Представление чисел с плавающей запятой (точкой)
- •1.5. Коды двоичных чисел
- •1.5.1. Прямой код
- •1.5.2. Обратный код
- •1.5.3. Модифицированный обратный код
- •1.5.4. Дополнительный код
- •2.1.1. Алгебраическое сложение чисел в дополнительном коде
- •2.1.2. Алгебраическое сложение чисел в обратном коде
- •2.1.3. Переполнение разрядной сетки при сложении чисел
- •2.2. Сложение (вычитание) двоичных чисел с плавающей запятой
- •2.2.1. Метод ускоренного сложения двоичных чисел с запоминанием переносов
- •2.3. Умножение двоичных чисел с фиксированной запятой
- •2.4. Машинные технологии выполнения операции умножения двоичных чисел с фиксированной запятой
- •2.5. Умножение двоичных чисел с плавающей запятой
- •2.6. Методы ускоренного выполнения операции умножения двоичных чисел
- •2.6.1. Метод пропуска такта суммирования
- •2.6.2. Метод анализа сомножителей
- •2.6.3. Метод расшифровки и одновременного умножения на два разряда множителя
- •2.6.4. Метод ускоренного умножения Мак-Сорли
- •2.6.5. Метод ускоренного умножения Лемана
- •2.6.6. Метод умножения с расшифровкой пар разрядов множителя и запоминанием переносов
- •2.7. Деление двоичных чисел с фиксированной запятой
- •2.8. Деление двоичных чисел с плавающей запятой
- •3. Основы десятичной компьютерной арифметики
- •3.1. Машинное кодирование десятичных чисел
- •3.2. Выполнение арифметических операций с десятичными числами
- •3.2.1. Сложение десятичных чисел в эвм
- •3.2.2. Умножение десятичных чисел в эвм
- •3.2.3. Ускорение умножения в -кодах
- •Деление десятичных чисел в эвм
- •4.2. Моделирование алгоритма сложения двоичных чисел
- •Различные случаи ненормализованных мантисс
- •4.3. Проектирование алгоритма умножения чисел
- •4.5. Проектирование алгоритма деления чисел
- •4.7. Разработка алгоритма вычисления квадратного корня
- •Определение 1. Пусть и произвольные множества. Соответствием называется тройка множеств
- •Свойства отношений
- •Эквивалентность
- •Толерантность
- •Отношения порядка
- •Самодвойственные функции
- •Монотонные функции
- •Линейные функции
- •Функции, сохраняющие константу
- •5.2.7. Минимизация булевых функций
- •Метод Блейка
- •Метод Квайна-Мак-Класки
- •Минимизация с использованием карт Карно
- •Дана функция четырех переменных (рис. 5.13):
- •Минимизация не полностью определенных булевых функций
- •Минимизация систем булевых функций
- •5.3. Методика синтеза комбинационных схем на логических элементах
- •5.3.1. Логические элементы
- •5.3.2. Общий алгоритм построения комбинационных схем
- •5.3.3. Синтез кс в классическом базисе
- •5.3.4. Синтез кс в базисах «и-не», «или-не»
- •5.3.5. Реализация кс в базисе Жегалкина
- •5.3.6. Синтез составных кс
- •Заключение
- •Библиографический список к главам 1, 2, 3, 4
- •Библиографический список к главе 5
Эквивалентность
На основании перечисленных выше свойств отношения можно разбить на отдельные группы, произвести их классификацию.
Определение 16. Эквивалентностью называют отношения, которые одновременно рефлексивны, симметричны и транзитивны, т.е.
(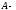 эквивалентность)
эквивалентность)
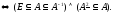
Таким образом, к эквивалентностям относятся такие отношения: «быть однополчанином», «быть членом той же партии, что и …», «быть тезкой», «быть единомышленником», «быть одной веры с …», «иметь тот же остаток при делении на 5», «и много, много других.
Отношение
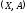 эквивалентности тесно связано с
разбиением множества
эквивалентности тесно связано с
разбиением множества
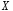 .
Эту связь отражает следующая теорема.
.
Эту связь отражает следующая теорема.
Теорема
4. Задание
отношения
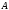 эквивалентности на конечном множестве
эквивалентности на конечном множестве
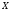 равносильно разбиению этого множества.
равносильно разбиению этого множества.
Доказательство.
Необходимость.
Пусть на конечном множестве
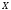 задано отношение эквивалентности с
областью истинности
задано отношение эквивалентности с
областью истинности
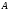 .
Проведем следующее построение.
.
Проведем следующее построение.
Выберем
некоторый элемент
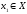 и построим подмножество
и построим подмножество
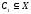 из всех элементов, эквивалентных
из всех элементов, эквивалентных
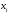 ,
т.е.
,
т.е.
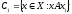 .
Из множества
.
Из множества
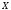 удалим все элементы, содержащиеся в
подмножестве
удалим все элементы, содержащиеся в
подмножестве
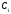 .
Получим множество
.
Получим множество
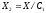 .
Если
.
Если
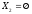 ,
то построение завершено. В противном
случае снова выберем некоторый элемент
,
то построение завершено. В противном
случае снова выберем некоторый элемент
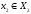 и, построив подмножество
и, построив подмножество
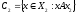 ,
удалим его из
,
удалим его из
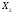 ,
получая множество
,
получая множество
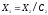 .
Процесс нашего построения будет завершен,
как только будет получено пустое
множество
.
Процесс нашего построения будет завершен,
как только будет получено пустое
множество
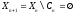 ,
а результатом этого построения станет
совокупность
,
а результатом этого построения станет
совокупность
 подмножеств
подмножеств
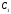 ,
,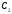 ,
…,
,
…,
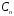 ,
которая, согласно нашему построению,
будет удовлетворять следующим условиям:
,
которая, согласно нашему построению,
будет удовлетворять следующим условиям:
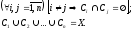
Следовательно,
данное множество {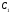 ,
,
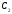 ,
…,
,
…,
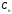 }
подмножеств множества
}
подмножеств множества
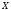 (согласно определению разбиения) есть
разбиение последнего. Необходимость
доказана.
(согласно определению разбиения) есть
разбиение последнего. Необходимость
доказана.
Достаточность.
Пусть теперь задано разбиение {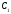 ,
,
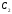 ,
…,
,
…,
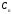 }
множества
}
множества
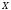 .
Рассмотрим на нем отношение «принадлежать
одному и тому же подмножеству». Данное
отношение рефлексивно (любой элемент
.
Рассмотрим на нем отношение «принадлежать
одному и тому же подмножеству». Данное
отношение рефлексивно (любой элемент
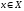 принадлежит тому же подмножеству, в
котором сам и находится), симметрично
(если
принадлежит тому же подмножеству, в
котором сам и находится), симметрично
(если
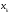 принадлежит тому же подмножеству, что
и
принадлежит тому же подмножеству, что
и
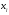 ,
то и
,
то и
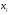 принадлежит тому же подмножеству, что
и
принадлежит тому же подмножеству, что
и
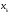 )
и, наконец, транзитивно (если
)
и, наконец, транзитивно (если
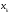 принадлежит тому же подмножеству, что
и
принадлежит тому же подмножеству, что
и
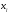 ,
а
,
а
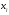 принадлежит тому же подмножеству, что
и
принадлежит тому же подмножеству, что
и
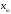 ,
то
,
то
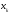 принадлежит тому же подмножеству, что
и
принадлежит тому же подмножеству, что
и
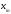 ).
Следовательно, данное отношение есть
эквивалентность. Теорема доказана.
).
Следовательно, данное отношение есть
эквивалентность. Теорема доказана.
Замечание
1. Данная
теорема легко распространяется на
случай бесконечного множества
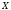 .
При этом алгоритм построения, описанный
в первой части доказательства, будет
работать сколь угодно долго, формируя
конечное или бесконечное множество
{
.
При этом алгоритм построения, описанный
в первой части доказательства, будет
работать сколь угодно долго, формируя
конечное или бесконечное множество
{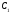 ,
,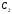 ,
…,
,
…,
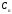 ,
…}.
,
…}.
Замечание
2. Формируемые
при работе описанного выше алгоритма
подмножества
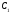 ,
,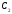 ,
…,
,
…,
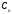 называют классами
эквивалентности.
Например, отношение «иметь тот же остаток
при делении на 5» разобьет множество
называют классами
эквивалентности.
Например, отношение «иметь тот же остаток
при делении на 5» разобьет множество
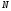 натуральных чисел на такие пять классов
эквивалентности:
натуральных чисел на такие пять классов
эквивалентности:
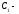 класс
чисел, кратных пяти (числа, остаток
которых при делении на 5 равен нулю);
класс
чисел, кратных пяти (числа, остаток
которых при делении на 5 равен нулю);
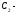 класс чисел с остатком при делении на
5, равным 1;
класс чисел с остатком при делении на
5, равным 1;
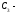 класс чисел с остатком при делении на
5, равным 2;
класс чисел с остатком при делении на
5, равным 2;
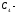 класс чисел с остатком, равным 3;
класс чисел с остатком, равным 3;
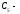 класс чисел с остатком, равным 4. Классами
эквивалентности отношения «иметь то
же социальное происхождение» будут
социальные группы: рабочие, служащие,
крестьяне и т.д.
класс чисел с остатком, равным 4. Классами
эквивалентности отношения «иметь то
же социальное происхождение» будут
социальные группы: рабочие, служащие,
крестьяне и т.д.
Замечание
3. Непересекаемость
классов эквивалентности (т.е. условие
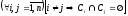 )
обеспечивает непротиворечивость деления
множества
)
обеспечивает непротиворечивость деления
множества
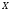 на классы (каждый элемент принадлежит
не более чем одному классу), а условие
на классы (каждый элемент принадлежит
не более чем одному классу), а условие
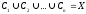 говорит о полноте системы этих классов
(любой элемент из
говорит о полноте системы этих классов
(любой элемент из
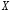 принадлежит
какому-либо классу).
принадлежит
какому-либо классу).
Замечание 4. Данная теорема имеет применение не только в математических науках. Любая научная теория так или иначе, связана с классификацией объектов, составляющих область ее исследований. Для успешного осуществления этой классификации необходимо найти отношение эквивалентности между объектами. Если будет найдено отношение, которое одновременно рефлексивно, симметрично и транзитивно, то оно определит непротиворечивую и полную классификацию изучаемого разнообразия.
Представляет определенный интерес рассмотреть последствия, к которым приводит отсутствие свойства транзитивности в рефлексивных и симметричных отношениях.
Вопросы для самоконтроля
-
Какие отношения из нижеследующих являются эквивалентностью? а) «быть того же цвета»; б) «быть кратным тому же числу»; в) «иметь тот же наибольший общий делитель»; г) «иметь хотя бы одно общее свойство».
-
Для приведенных выше отношений эквивалентности определите их классы эквивалентности.
