Линейные структуры

К линейным структурам относятся: массивы, последовательности, таблицы.

Порядок следования (и, соответственно выборки) элементов таких структур имеет линейный характер и соответствует порядку расположения элементов в памяти: один за другим без каких-либо промежутков. Адрес элемента соответствует его положению и определяется индексом – порядковым номером элемента в последовательности размещения.

Особенностью линейной структуры является то, что при последовательной организации (размещении) одна допускает возможность прямого доступа к произвольному элементу, поскольку условие однородности однотипности) предполагает, что все элементы занимают расположение строго последовательно области одинакового физического адреса элемента по значению его индекса.

Массив представляет собой совокупность однотипных элементов причем число элементов массива известно до его размещения, что позволяет строить гибкие многомерные системы адресации.

Последовательность также как и массив это совокупность однотипных элементов, однако, число элементов до размещения неизвестно, хотя каждая конкретная последовательность имеет конечную длину до начала обработки. Необходимо считать длину последовательности бесконечной.

Таблица это последовательность обычно представляется строками,. совокупностью различных элементов, иначе это множество записей каждая из которых представляет набор поименованных полей. С точки зрения размещения элементов таблица может быть представлена как одномерный массив с однородными композиционными элементами, каждый из которых представляет собой совокупность разнотипных элементов.

Кроме того, разнотипность элементов позволяет ввести отличную от перечислительной схему идентификации записей, определив одно из полей как ключ записи.

Нелинейные структуры

К нелинейным структурам относятся: списки, деревья и сети.

Порядок следования (и. соответственно, выборки) элементов таких структур может не соответствовать прядку расположения элементов в памяти. Списки представляют собой пример линейного упорядочения, а деревья двумерного упорядочения, сети, - произвольного. Соответственно различаются методы и средства, обеспечивающие последовательность выборки элементов данных.

Списки представляют собой совокупность однотипных элементов, однако, прядок выборки элементов может отличаться от порядка следования в памяти, определенного при размещению. Наиболее очевидный способ установления однонаправленного порядка выборки элементов – это сопоставить каждому элементу списка ссылку, указывающую на следующий элемент. Соответственно, для организации двунаправленного списка допускающего так же выборку в обратном порядке. Каждый элемент должен иметь ссылку на предыдущий. Такая организация уже не допускает возможности прямого доступа. Число элементов списка как и в си. последовательности пожжет быть неизвестна до размещения до начала обработки необходимо считать длину списка бесконечный, что ведет к необходимости предусматривать спец. процедуру выделения памяти. Таким образом с точки зрения физической реализации элемент списка должен быть составным, включающий собственно информативно данные несущие смысловое значение и дополнительные данные (ссылки) определяющие порядок доступа к информативным элементам. В общем си ссылки могут указывать ответвления к другим спискам- подспискам в зависимости от способа построения списка и предполагаемых путей доступа различают несколько видов ссылок:

1. перекрестные

2. боковые

3. иерархические

4. множественные

Что позволяет изменять «естественный» последовательный порядок прохода по элементам списка.

Деревья представляют собой иерархию элементов называемую узлами на самом верхнем уровне иерархии есть только один узел, так называемый корень. Каждый узел кроме корня связан с одним узлом на более высоком уровне, называется исходным узлом для данного узла. Каждый элемент имеет только один исходный узел. Каждый элемент может быть связан одним или несколькими элементами на более низком уровне, которые называются порожденные. Элементы, расположенные в конце ветви, то есть не имеющие порожденных называются листьями

Деревья могут быть: упорядоченными, которые делятся на:

• сбалансированные

• двоичные

• несбалансированные

Сбалансировано дерево имеет одинаковое число ветвей в каждом узле при чем процесс включения новых ветвей в узлы идет с верху в низ, а на каждом корне дерева слева направо. Для дерева с фиксированным числом ветвей физическая организация данных будет долее простая, но большая часть логической организации данных не может быть создана в виде сбалансированной древовидной структуры и для представ. треб. переменное число ветвей в каждом узле. В то же время индексы могут быть построены в виде сбалансированных древовидных структур.

Сбалансированное дерево

Несбалансированное дерево

Двоичные деревья - это особая категория сбалансированных древовидных структур в которой допускается не более двух ветвей для одного узла.

Любые связи в дереве можно представить в виде двоичных древовидных структур. При таком представлении каждый элемент может иметь указатели как на порожденные, так и на подобные элементы.

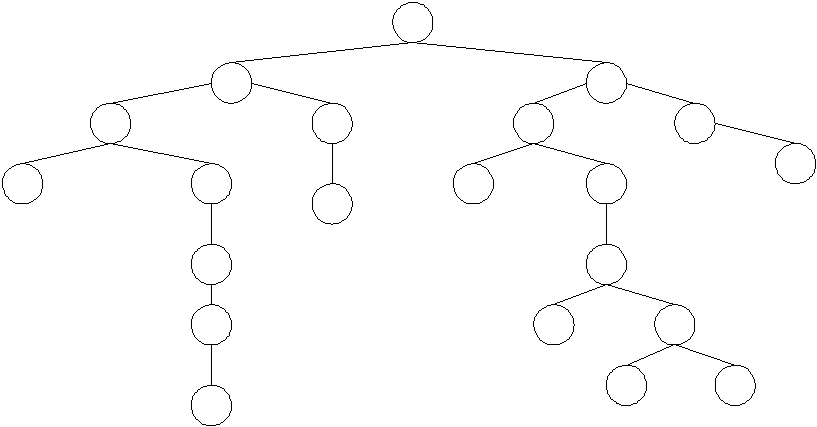
Несбалансированное двоичное дерево