1.2. Каноническое разложение и спектральное представление случайной функции.

Метод канонических разложений состоит в том, что случайная функция представляется в виде суммы элементарных случайных функций . Последние представляют собой произведения некоторых случайных величин и неслучайных функций :

.

Таким образом, при каноническом разложении случайная функция представляется в виде

, (1.5)

где — математическое ожидание функции ; V_k — некоррелированные случайные величины с нулевыми математическими ожиданиями.

Корреляционная функция с учетом некоррелированности случайных величин V_i (ковариации этих величин K_ij= 0 при ) будет

(1.6)

где — дисперсия случайной величины V_i.

Зависимость (1.6) называется каноническим разложением корреляционной функции.

Можно показать, что если задано каноническое разложение корреляционной функции в виде (1.6), то для случайной функции каноническое разложение имеет вид (1.5), а случайные величины V_i имеют дисперсии .

Поскольку корреляционная функция является четной функцией , то в достаточно большом временном интервале от -Т до +T (рис. 1.7) ее можно разложить в ряд Фурье по четным (косинусным) гармоникам, а именно:

. (1.7)

Здесь коэффициенты разложения с учетом четности равны

. (1.8)

Рис. 1.7. Корреляционная функция на интервале от –T до +T.

Дисперсию случайной функции, имеющей корреляционную функцию , заданную коэффициентами разложения (1.8), можно определить по формуле (1.7) при :

.

Если в качестве элементарной случайной функции принять

, (1.9)

а выражение (1.5) рассматривать как ряд Фурье, то стационарный СП может быть представлен таким каноническим разложением

. (1.10)

Здесь U_k и V_k — некоррелированные случайные величины с нулевыми математическими ожиданиями и одинаковыми дисперсиями , определяемыми по формулам (1.8).

Каноническое разложение (1.10) называют также спектральным разложением (представлением) стационарного СП.

Исходя из этих свойств U_k и V_k, определим математическое ожидание, корреляционную функцию и дисперсию элементарной случайной функции

;

.

Таким образом, дисперсия случайной функции Х(t), представленной в каноническом виде (1.10), равна сумме дисперсий элементарных случайных функций , которые являются одновременно коэффициентами разложения корреляционной функции стационарной случайной функции Х(t) в ряд Фурье:

. (1.11)

Зная вид корреляционной функции k_x(), можно получить дисперсии коэффициентов канонического разложения V_k и U_k, а также частоты _k стационарного СП Х(t).

Рассмотрим спектральное разложение стационарного СП в комплексной форме. С помощью формул Эйлера для комплексных чисел

(i —мнимая единица) элементарный стационарный СП вида (1.10) может быть записан в комплексной форме

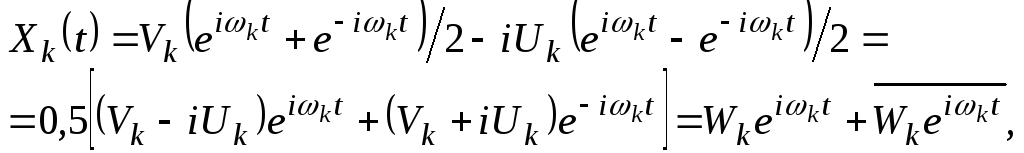(1.12)

где (1.13)

Горизонтальная черта над буквенными обозначениями комплексных величин означает здесь и далее операцию сопряжения.

Покажем, что выражение (1.12) представляет собой каноническое разложение элементарного стационарного СП в комплексной форме, т.е. что дисперсия равна , а - некоррелированные случайные величины с нулевыми математическими ожиданиями. Из (1.13) следует, что

так как . Аналогично получим:

Покажем, что случайные величины не коррелированны. Ковариацию этих случайных величин определим как математическое ожидание произведения на комплексно-сопряженную случайную величину :

так как .

Найдем дисперсию случайной величины как математическое ожидание квадрата модуля :

Аналогично,

Корреляционная функция элементарного стационарного СП (1.10) имеет вид

.

Поскольку то

. (1.14)

Выражение (1.14) представляет собой разложение корреляционной функции элементарного стационарного СП в комплексной форме.

Следовательно, спектральное разложение стационарного СП (1.10) в комплексной форме имеет вид

.

Здесь учтено, что

Корреляционная функция этого СП

(1.15)

Рассмотрим, как будет преобразовываться спектральное разложение (1.10) при неограниченном увеличении интервала разложения (T). Введем в рассмотрение частотный интервал  между соседними гармониками, частоты которых равны и . Представим разложение (1.10) в таком виде:

.

Рассмотрим предел этого выражения при  0. Введем обозначения:

.

Тогда при T  (0 и k0) получим интегральное каноническое представление стационарного СП:

,

где V() и U() —случайные функции непрерывного аргумента  - частоты.

Такая модель случайного процесса часто используется при решении прикладных проблем теории случайных функций. В этой теории 1 показывается, что случайные функции V() и U() представляют собой специфический процесс (белый шум) с характеристиками

,

где S_x() —некоторая неотрицательная функция частоты , называемая спектральной плотностью стационарного СП Х(t) (определение которой будет дано ниже), ( )—дельта-функция.

Интегральное представление стационарного СП может производиться и в комплексной форме с помощью интеграла Фурье:

. (1.16)

Выясним, какими свойствами должна обладать функция для того, чтобы стационарный СП Х(t), корреляционная функция которого должна зависеть от разности моментов времени, мог бы быть представлен в таком виде. Рассмотрим корреляционную функцию

подынтегральное выражение которой будет зависеть от разности моментов времени, если корреляционная функция равна произведению спектральной плотности СП Х(t) на функцию

. (1.17)

В этом случае после интегрирования по в выражении для получим