Центрированной случайной величиной называют величину

, (1.13)

т. е. отклонение случайной величины от среднего значения.

Моменты центрированной случайной величины называются центральными моментами. Так, центральный момент s-го порядка будет

. (1.14)

Очевидно, что центральный момент первого порядка равен нулю.

Наиболее важное для приложений значение имеет центральный момент 2-го порядка, который называется дисперсией случайной величины и обозначается :

. (1.15)

Дисперсия случайной величины есть характеристика рассеивания значений случайной величины около ее математического ожидания.

С геометрической точки зрения дисперсия представляет момент инерции площади под кривой распределения относительно вертикальной оси, проходящей через центр тяжести этой площади. Дисперсия имеет размерность квадрата случайной величины.

Обычно в качестве характеристики рассеивания рассматривают среднее квадратичное отклонение случайной величины (эту характеристику называют также стандартом случайной величины), которое определяется квадратным корнем из дисперсии (). Стандарт имеет размерность случайной величины. Используется также безразмерная характеристика рассеивания – коэффициент вариации , равный отношению стандарта к математическому ожиданию ().

1.3. Законы распределения случайных величин

1. Закон равномерного распределения. Если возможные значения непрерывной случайной величины лежат в пределах некоторого определенного интервала и, кроме того, известно, что в пределах этого интервала все значения случайной величины одинаково вероятны, то о такой случайной величине говорят, что она распределена равномерно (рис. 1.3).

Рис. 1.3. Вид плотности вероятности при равномерном распределении.

В этом случае

(1.16)

где а — плотность распределения; — интервал возможных значений случайной величины.

Математическое ожидание и дисперсия случайной величины X, распределенной равномерно на интервале :

.

2. Нормальный закон распределения (закон Гаусса). Этот закон распределения случайных величин занимает особое место в механике. Плотность вероятности при нормальном законе распределения имеет вид

, (1.17)

где т и  — математическое ожидание и стандарт случайной величины X.

Вид кривой распределения при нормальном законе показан на рис. 1.4.

Из рисунка видно, что чем больше дисперсия и стандарт случайной величины, тем меньше наибольшая ордината р(х) и тем больше растягивается кривая распределения вдоль оси абсцисс.

1.4. Плотности вероятностей р(х) гауссовских случайных величин, соответствующие различным значениям стандарта .

Вычислим вероятность попадания случайной величины X, подчиненной нормальному закону, на участок от до :

. (1.18)

Производя замену переменных , получим плотность нормированного нормального распределения, стандарт которого равен единице (_u = 1):

.

Плотность такого распределения представлена на рис. 1.4 в виде кривой, соответствующей значению  = 1. Табулированные значения этой плотности приводятся в справочниках по математике. Табулируются также значения функции

, (1.19)

которую называют интегралом вероятностей или функцией Лапласа.

С учетом этого интеграла для вероятности попадания любой нормальной случайной величины X с центром m и дисперсией ² в интервал взамен (1.17) можно записать

. (1.20)

Наряду с функцией часто используется так называемая функция ошибок

,

с помощью которой вероятность попадания величины X в интервал записывается так

.

В связи с нечетностью функции ошибок, для определения вероятности попадания случайной величины на участок, симметричный относительно математического ожидания (рис. 1.5), используется выражение

.

Рис. 1.5. К вычислению вероятности попадания случайной величины на заданный участок.

Рис. 1.6. К вычислению вероятности отклонения случайной величины от математического ожидания на один, два и три стандарта.

Используя таблицы функции ошибок, можно оценить вероятность отклонения случайной величины от математического ожидания более чем на n стандартов  (рис. 1.6):

. (1.21)

В частности, вероятность превышения случайной величиной значения т + 2 (n=2) составляет 0,02, а значения т + З (n=3) примерно равно 0,0015. Поэтому говорят, что отклонение случайной величины, подчиненной нормальному закону, от ее математического ожидания на величину трех стандартов практически определяет наибольшее значение случайной величины.

Практическая значимость нормального распределения в первую очередь вытекает из центральной предельной теоремы теории вероятностей. Эта теорема не строго формулируется следующим образом: если случайная величина X есть сумма n статистически независимых случайных величин с произвольными плотностями, то ее плотность приближается к нормальной плотности (1.17), если n стремится к бесконечности. Случайные явления очень часто являются результатом воздействия многих независимых случайных факторов, поэтому нормальное распределение часто служит хорошей аппроксимацией плотностей случайных величин и процессов. Так, например, можно считать подчиненными этому закону ординаты морского волнения в данном режиме, ординаты волновых моментов, действующих в поперечных сечениях водоизмещающих судов, величины пределов текучести и прочности материала при испытаниях большого количества образцов и т. д.

Кроме того, удобство практического использования такой аппроксимации предопределяется наличием в ней всего двух параметров (т и ), а также тем фактом, что различные линейные операции, такие как дифференцирование, интегрирование и преобразование Фурье, выполняемые над нормально распределенными случайными величинами, дают в результате нормально распределенные величины.

3. Закон логарифмически нормального (логнормального) распределения. Рассмотрим случайные величины, связанные соотношением Y = lgX. Если случайная величина Y распределена нормально, а ее математическое ожидание и стандарт равны соответственно, то плотность логарифмически нормального распределения величины X имеет вид

. (1.22)

Характер поведения функции показан на рис. 1.7.

Рис. 1.7. Вид плотности вероятности f(x) при логнормальном законе распределения.

4. Закон Рэлея. Этот закон устанавливает распределение амплитуд случайного узкополосного гауссовского процесса. Ему практически подчиняются амплитуды и высоты волн в данном режиме нерегулярного волнения, а также амплитуды вызванных процессов, связанных линейно с волнением (например, амплитуды качки и волновых моментов водоизмещающих судов).

Плотность вероятности случайной величины A, распределенной по закону Рэлея имеет вид

, (1.23)

где параметр  связан с математическим ожиданием m_a случайной величины A зависимостью

.

По смыслу величина а является положительной, т. е. а > 0. Вид кривой распределения Рэлея показан на рис. 1.8. Наибольшая ордината плотности вероятности соответствует а=.

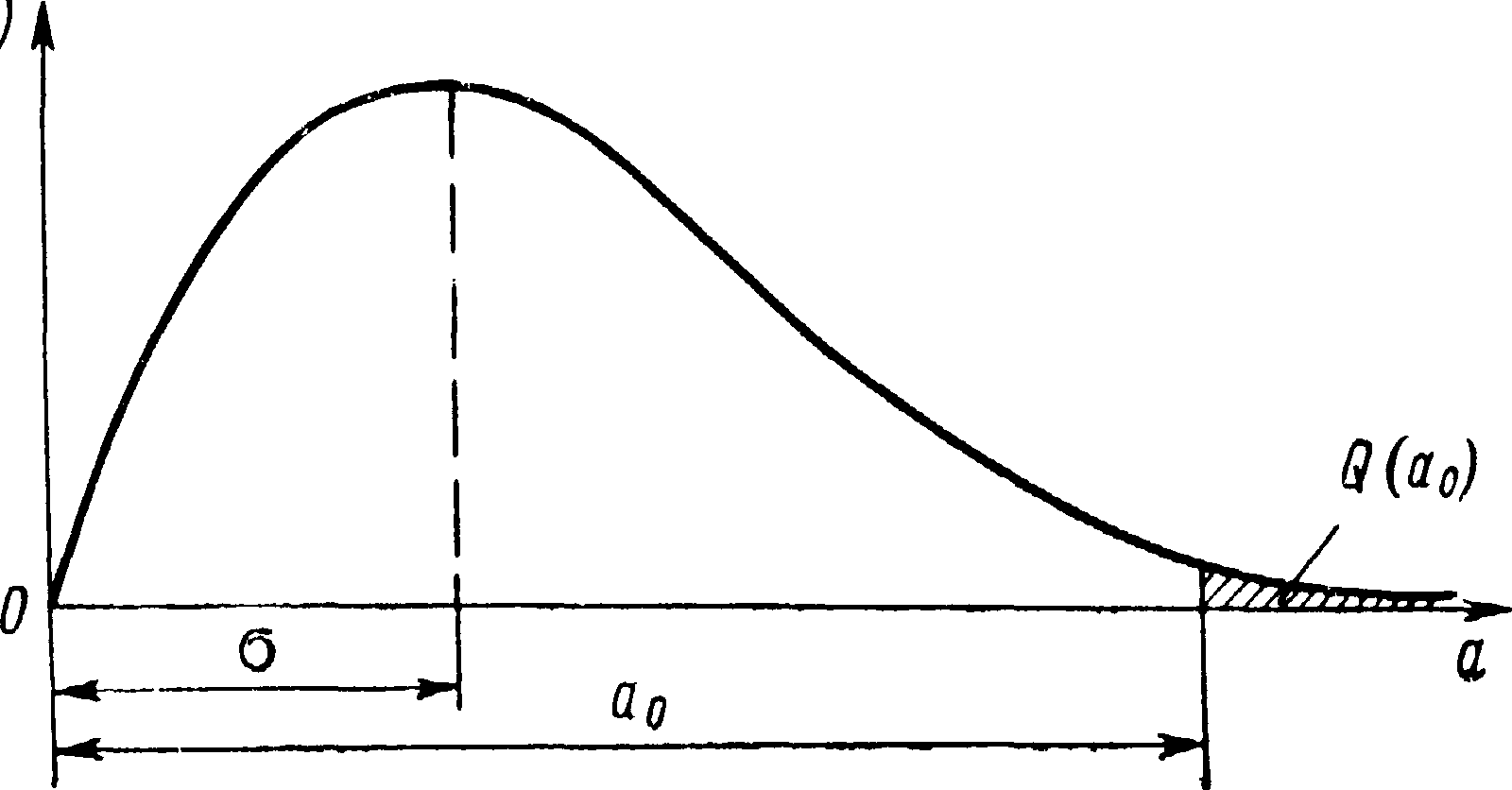
Рис. 1.8. Вид плотности вероятности по закону Рэлея.

Функция распределения для закона Рэлея, т. е. вероятность того, что амплитуда а будет меньше некоторой величины , запишется в виде

. (1.24)

Соответственно вероятность превышения величины , которая называется обеспеченностью, будет

.

Логарифмируя (1.25), можно выразить значение через величину обеспеченности Q:

. (1.25)

5. Экспоненциальное (показательное) распределение. Случайная величина X имеет экспоненциальное распределение (рис. 1.9) с параметром >0, если

Рис. 1.9. Вид плотности вероятности f(x) при экспоненциальном законе распределения.

Математическое ожидание и дисперсия случайной величины X

Покажем, что если случайная величина a подчиняется закону Рэлея, то ее квадрат подчиняется экспоненциальному закону.

Используя правило функционального преобразования плотности вероятности случайных величин, связанных функциональной зависимостью, [ ] на основании формулы (1.23) получим

. (1.26)

5. Распределение Вейбулла-Гнеденко. Случайная величина X имеет распределение Вейбулла-Гнеденко (рис. 1.10) с параметрами , если ее плотность вероятности равна

(1.27)

Здесь - параметр формы; Т₀ - параметр масштаба.

Рис. 1.10. Вид плотности вероятности f(x), соответствующей закону Вейбулла-Гнеденко, при различных значениях параметра .

Функция распределения имеет вид

.

Математическое ожидание и дисперсия случайной величины X равны

(1.28)

Здесь - гамма-функция.

Вариация двух параметров этого распределения обеспечивает хорошую аппроксимацию очень широкого класса фактических зависимостей, получаемых при решении различных вероятностных задач механики. Распределение при  >1 имеет моду, а при моды не имеет. При = 1 это распределение вырождается в экспоненциальное.