Добавил:

Uman Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Московский государственный технический университет им. H.Э.Баумана

Предмет:

Высшая математика

Файл:

answers

.pdf

Источник:

https://studizba.com

Скачиваний:

Добавлен:

04.03.2014

Размер:

316.93 Кб

Скачать

☆

1 / 21 2 > Следующая >>>

Билет 1

Лекция 22. Однородные системы линейных дифференциальных уравнений с постоянными коэффициентами.

Система линейных дифференциальных уравнений с постоянными коэффициентами может быть записана в виде

		a11 ...		a1n			y1
y Ay , где A						y
y Ay , где A		... ....		...	,	y	...	(векторная форма записи)

		an1 ...		ann			yn
или
y1 a11 y1	... a1n yn
....................................			(покоординатная форма записи).
yn an1 y1	... ann yn
							1

Будем искать решение системы в виде y			e x ,				...	.

							n
Подставляя y в уравнение системы, получаем

e x Ae x ,		e x A 0,						A .
Получено уравнение для определения соответствующего собственному значению									собственного вектора ( 0) линейного оператора с матрицей A .

Система уравнений

A или A E 0

имеет ненулевое решение только, когда определитель системы равен нулю, т.е.

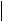A E 0 .

Это – характеристическое уравнение системы линейных дифференциальных уравнений с постоянными коэффициентами. В развернутом виде его можно записать так:

a11	a12	...	a1n
a21	a22	...	a2n	0 .
...	...	...	...
an1	an2	...	ann

Характеристическое уравнение представляет собой алгебраическое уравнение n - го порядка относительно . Из основной теоремы высшей алгебры известно, что

оно имеет ровно n корней. Часть корней может быть действительными корнями, часть - комплексными, но комплексные корни встречаются только парами комплексносопряженных корней. Это следует из действительности коэффициентов характеристического уравнения и теорем Виета.

1) Рассмотрим случай, когда все собственные значения 1,... n линейного оператора с матрицей A (или все характеристические числа матрицы A , что одно и то же) действительны и различны.

Из линейной алгебры известно, что действительным различным собственным значениям 1,... n соответствуют линейно независимые собственные векторы

1 ,..., n , которые можно определить по собственным значениям из системы уравнений

A или A E 0 .

В развернутом виде эти уравнения для k ,
	k можно записать в виде

a11 k

...

a1n

...	a1n
...	...
...	ann k

	k	0
1

	...	... .
	k
	n
		0

Теперь решения системы линейных однородных уравнений с постоянными коэффициентами будут

x 1

e 1

,...., y

Проверим, что решения являются линейно независимыми. Составим определитель Вронского

y1 ...

...

W ... ... ...

...

... exp(

...

x) 0 , так как векторы

,..., n линейно независимы и

y1n ...

ynn

...

определитель из координат этих векторов отличен от нуля. Так как определитель Вронского отличен от нуля, то полученные решения линейно независимы. Так как этих решений ровно n, то они составляют фундаментальную системурешений. Следовательно, общее решение системы линейных однородных уравнений может быть записано в виде

														n

yoo		C1 y1 ... Cn yn										Ck e k x k .
														k 1
			x x 4y							1				4

Пример.			y x		2y		,	A							,
			y x		2y					1					2
A E 1									4					2 6 0,						3,				2	2
					1 2																1			2
					1 2
	3,				4	4 1						0,				1 1		,		1
	3,								1			0,				1 1		,	1			,
1									1						1		2
					1	1 2															1
		2,		1			4					2			0,	2	4 2		,			4
	2	2,									1				0,	2	4 2		,	2			,
	2				1			4				2				1		2				1
					1			4				2										1
					1			C					4
y	oo	C e 3t						C		2	e2t .
	oo		1							2
						1							1

xC1e 3t 4C2e2t

yC1e 3t C2e2t

Билет 2

Лекция 21. Системы линейных дифференциальных уравнений.

Неоднородную систему линейных дифференциальных уравнений можно записать в виде

y A x y f x .

Однородную систему линейных дифференциальных уравнений можно записать в виде

y A x y .

Все теоремы для линейных систем аналогичны соответствующим теоремам для линейных дифференциальных уравнений высших порядков. Этого и следовало ожидать, так как система дифференциальных уравнений сводится к дифференциальному уравнению высшего порядка.

Теоремы о свойствах решений однородной и неоднородной системы.

Если

yo1 ,

yo2 - решения однородной системы, то yo1 y02 , yo1 , y02 - решения однородной системы.

Если

y0, yн - решения однородной и неоднородной систем, то

yн - решение неоднородной системы.

Если yн1 ,

yн2 - решения неоднородной системы, то yн1 yн2 - решение однородной системы.

Доказательство.

yo1 yo2

y01

y02

A x yo1 A x y02

A x y01 y02

y01

y01 A x y01

A x y01

yo yн A x y0 A x

yн

A x y0

yн

f x

yн1 yн2

yн1

yн2

A x yн1

f x A x y

н2 f x

A x yн1

yн2

билет 3

Любые n линейно независимых решений однородной системы представляют собой базис в пространстве решений и называются фундаментальной системой решений однородной системы.

Матрица Y x , составленная из этих решений detY x W x 0 , называется фундаментальной матрицей однородной системы.

Теорема о структуре общего решения однородной системы.

Общее решение однородной системы представляет собой линейную комбинацию решений фундаментальной системы решений.

yoo x C1 y1 x ... Cn yn x .

Доказательство. Проверим, что yoo x C1 y1 x ... Cn yn x является общим решением, исходя из определения общего решения.

1) yoo x C1 y1 x ... Cn yn x - решение однородной системы как линейная комбинация ее решений (теорема о свойствах решений).

		y01
	Зададим произвольные начальные условия y0			C1 ,...Cn , при
2)	Зададим произвольные начальные условия y0	...	и покажем, что можно единственным образом выбрать набор констант	C1 ,...Cn , при

		y0n
	котором yoo x0 C1 y1 x0 ... Cn yn x0 y0 . Запишем это соотношение покоординатно как			систему уравнений

относительно C1 ,...Cn .

C1 y11 x0 ...Cn yn1 x0 y01 C1 y12 x0 ...Cn yn2 x0 y02

..........................................

C1 y1n x0 ...Cn ynn x0 y0n

Определитель этой системы равен W x0 0 , так как решения линейно независимы. Поэтому набор констант C1 ,...Cn определяется из системы уравнений единственным образом. Теорема доказана.

Билет 4

Теорема о структуре общего решения неоднородной системы.

Общее решение неоднородной системы равно сумме общего решения однородной системы и частного решения неоднородной системы.

yoн x yoo x yчн x

Доказательство. 1) yoн x yoo x yчн x - решение неоднородной системы по теореме о свойствах решений.
2) Зададим произвольные начальные условия yoн x0 y0 . Выберем какое-либо частное решение неоднородное системы		yчн x и вычислим для него
начальные условия в x0 yчн x0 . Составим систему уравнений yoo x0 yoн x0 yчн x0 u и запишем ее покоординатно.
C1 y11 x0 ...	Cn yn1 x0 u1
...............................................

C1 y1n x0 ... Cn ynn x0 un

Определитель этой системы – определитель Вронского, он не равен нулю, так как составлен из линейно независимых решений, составляющих фундаментальную систему решений. Следовательно, набор констант из этой системы уравнений определяется однозначно. Теорема доказана.

Билет 5

y n

Метод	вариации		произвольной постоянной для линейного	неоднородного	дифференциального	уравнения n-ого порядка.
a1 x y n 1		... an 1 x y an x y f x . ( y n		Ly f x ).
Здесь	обозначено		L a1 x y n 1 ... an 1 x y an x y , заметим,		если y - решение	однородного уравнения, то

Ly .

Заметим, всегда, применяя метод вариации, надо делить на коэффициент при старшей производной, т.е. приводить уравнение.

Пусть найдено решение однородного уравнения

yoo x C1 y1 x ... Cn yn x .

Варьируем произвольные постоянные, ищем решение неоднородного уравнения в виде

yoн x C1 x y1 x ... Cn x yn x .

Дифференцируем это соотношение

yoн x C1 x y1 x ... Cn x yn x C1 x y1' x ... Cn x yn' x .

Потребуем, чтобы

C1 x y1 x ... Cn x yn x 0 .,

тогда yoн x C1 x y1' x ... Cn x yn' x .

Дифференцируем еще раз

yoн x C1 x y1' x ... Cn x yn' x C1 y1'' x ...Cn yn'' .

Потребуем, чтобы

C1 x y1 x ... Cn x yn x 0 .,

тогда yoн x C1 x y1'' x ... Cn x yn'' x .

Вновь дифференцируем и т.д., в результате, после n-2 дифференцирования получим

C1 x y1 n 2 x ... Cn x yn n 2 x 0 .

yoн n 1 x C1 x y1n 1 x ... Cn x ynn 1 x .

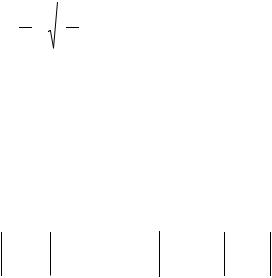
Дифференцируем и подставляем

+ C x y n 1 x

x y

n x C y n

... C

y n

... C

n 1 x .

oн

в неоднородное уравнение

yn Ly f x .

C y n ... C

y n + C

x y

n 1

x ... C

x y

n 1 x = L C y

...C

f x

1 1

Так как y ,..., y

- решения однородного уравнения, то y n Ly

0,k 1,...n .

Получим C '

n 1

... C '

y n 1 f x .

Это – последнее уравнение системы для определения варьированных констант. Соберем все уравнения в систему для определения констант.

x y

... C

x y

0 .,

x y

x ... C

x y

x 0 .,

........................................................

f x .

C '

y n 1

... C ' y n 1

Так как определитель системы – определитель Вронского, не равный нулю в силу линейной независимости решений, то функции C1 x ,...Cn x определяются

из этой системы однозначно.

yoн x C1 x y1 x ... Cn x yn x .

Теперь общее решение неоднородного уравнения определяется по формуле

Билет 6

Первые интегралы.

Пусть выполнены условия теоремы Коши. Рассмотрим решение задачи Коши

y x, x0 при заданных начальных условиях

y x0 y0 . По теореме Коши

оно существует и единственно.

Это решение

y x, x0 , y0 можно представить себе как некоторую интегральную кривую, соединяющие точки x0 , y0 ,

x, y .

Если в качестве начальных условий выбрать y x y , то по теореме Коши через эту точку проходит та же единственная интегральная кривая, ее уравнение

можно записать в виде

y0 x0 , x, y . Зафиксируем x0 ,

обозначим

C y

0 , получим соотношение x,

y C – общий интеграл системы

дифференциальных уравнений (векторное соотношение). Первый интеграл системы дифференциальных уравнений – скалярная составляющая общего интеграла. Общий интеграл системы дифференциальных уравнений – векторная функция, сохраняющая свое значение на решениях системы. Первый интеграл системы дифференциальных уравнений – скалярная функция, сохраняющая свое значение на решениях системы.

Знание одного первого интеграла позволяет понизить порядок системы на единицу. Знание общего интеграла дает общее решение системы, если только можно разрешить уравнение x, y C относительно y .

Билет 7

Рассмотрим линейное однородное дифференциальное уравнение с постоянными коэффициентами второго порядка

y py qy 0 .

Будем искать его решение в виде

y ekx . Подставляя y в дифференциальное уравнение, получим

ekx k 2 pk q 0. Так как ekx

0, то имеем

k 2 pk q 0 - характеристическое уравнение. Решая его, получим корни

k1,2

q .

Возможно три случая:

1) k1 , k2

действительны и различны,

i ,

i - комплексно сопряженные корни,

k2 - действительный кратный корень.

В случае действительных, различных корней получаем решения

y ek1x , y

ek2 x .

Для того, чтобы доказать, что решения составляют фундаментальную системурешений и общее решение записывается в виде

C ek1x

ek2 x ,

надо проверить линейную независимость y1 , y2 . Составим определитель Вронского

W y1

ek1x

ek2 x

e k1 k2 x

1 k1

k2 e k1 k2 x

0 , так как

ek1x

ek2 x

k1 k2 .

Заметим, что для уравнения второго порядка проверять линейную независимость можно проще. Надо показать,

что

m const . Тогда столбцы

определителя Вронского линейно независимы и W 0 . В нашем случае k1 i , k2 i при k1

k2 .

В случае комплексно сопряженных корней k1 i ,

k2 i , применяя формулу Эйлера

eiz

cos z i sin z, получим

комплексно сопряженные решения y e x

cos x i sin x ,

e x cos x i sin x . Так как линейная комбинация решений

линейного однородного уравнения тоже является

решением, то y

e x cos x,

e x sin x

являются решениями. Они линейно независимы, так как	y1	ctg x 0 .
	y2

Следовательно, общее решение линейного дифференциального уравнения с постоянными коэффициентами в случае комплексных корней можно записать по формуле

yoo e x C1 cos x C2 sin x .

В случае кратного действительного корня k

k одно из решений можно выбрать в форме y

ekx .

Второе решение будем выбирать в виде

u x ekx

. Подставим в дифференциальное уравнение, чтобы определить u x .

kue

ku ,

u e

2ku

u e

y2 e

2ku

u p u

ku qu e

pk q 0

p 2k u k

Так

как k

корень характеристического

уравнения,

то k 2 pk q 0 .

Так

как

k еще

кратный

корень,

то по

теореме Виета

k1 k2

k k 2k p . Поэтому

p 2k 0 .

Для

определения

u x имеем

уравнение

0 ,

отсюда

u x ax b .

Выберем a 1, b 0 , получим u x x .

Следовательно,

u x ekx

xekx . Решения

y , y

линейно независимы, так как

x m .

Поэтому общее решение линейного дифференциального уравнения с постоянными коэффициентами в случае кратного корня можно записать по формуле

yoo ekx C1 C2 x .

		Билет 8
	Задача Коши.
	Найти решение системы y f x, y , удовлетворяющее заданным начальным условиям y0		y x0 .
	Теорема Коши о существовании и единственности решения задачи Коши
	Пусть функция	f x, y непрерывна по совокупности переменных. Пусть	существуют и непрерывны частные производные
fk ,	k 1,...n,	s 1,...n
ys

Тогда существует и единственно решение задачи Коши.

					Билет 9
Метод	вариации	произвольной	постоянной	для	линейного	неоднородного	дифференциального	уравнения	n-ого	порядка.

y n

a1 x y n 1	... an 1 x y an x y f x . ( y n Ly f x ).
Здесь обозначено	L a1 x y n 1 ... an 1 x y an x y , заметим, если y - решение однородного уравнения, то

Ly .

Пусть найдено решение однородного уравнения

yoo x C1 y1 x ... Cn yn x .

Варьируем произвольные постоянные, ищем решение неоднородного уравнения в виде

yoн x C1 x y1 x ... Cn x yn x .

Дифференцируем это соотношение

yoн x C1 x y1 x ... Cn x yn x C1 x y1' x ... Cn x yn' x .

Потребуем, чтобы

C1 x y1 x ... Cn x yn x 0 .,

тогда

x C

x y

' x ... C

x y'

x .

oн

Дифференцируем еще раз

oн

x C

x y

' x ... C

y' x

C y'' x ...C

y'' .

Потребуем, чтобы

x y

x ... C

x y

x 0 .,

тогда

x C

x y'' x ... C

x .

oн

Вновь дифференцируем и т.д., в результате, после n-2 дифференцирования получим

x y

n 2 x

... C

x y

n 2 x 0 .

oн

n 1 x C x y n 1 x

... C

x y n 1 x .

Дифференцируем и подставляем

x y

oн

n x

C y n

... C

y n

+ C

n 1 x

... C

n 1 x .

1 1

в неоднородное уравнение

yn Ly f x .

C y n ... C

y n

+ C

x y

n 1

x ... C

x y

n 1 x = L C y

...C

f x

1 1

Так как y ,..., y

- решения однородного уравнения, то y

0,k 1,...n .

Получим C '

n 1

... C '

y n 1 f x .

1 1

C1 x y1 x ... Cn x yn x 0 .,

C	x y x ...		C			x y	x 0 .,
1	1				n		n
........................................................						f x .
C '	y n 1	... C '		y n 1		f x .
1	1	n		n
Так как определитель системы – определитель Вронского, не равный нулю в силу линейной независимости решений, то функции C1 x ,...Cn x определяются
из этой системы однозначно.								yoн x C1 x y1 x	Cn x yn x .
Теперь общее решение неоднородного уравнения определяется по формуле								yoн x C1 x y1 x	Cn x yn x .
							Билет 10
Одной из основных задач является также задача Коши - задача отыскания частного решения дифференциального уравнения, удовлетворяющего заданным начальным
условиям x0 , y0 G или интегральной кривой, проходящей через заданную точку x0 , y0 G .
Теорема существования решения задачи Коши.
Пусть функция		f x, y непрерывна в области x,y G ,						тогда существует хотя бы одно решение, удовлетворяющее любым заданным начальным

условиям x0 , y0 G или существует хотя бы одна интегральная кривая, проходящая через точку x0 , y0 G .

Теорема существования и единственности решения задачи Коши.

Пусть функция f x, y непрерывна в области x,y G и удовлетворяет в этой области одному из трех условий:

А: функция f x, y удовлетворяет условию Липшица по		y :
f x,y1 f x,y2 L y1 y2 ,
	f x, y
В: существует и ограничена частная производная	y	,
	f x, y
D: существует и непрерывна частная производная	y .

Заметим, что из условия D следует условие В., а из условия В следует условие А. Поэтому класс функций, удовлетворяющих условию А, шире, чем класс функций, удовлетворяющих условию В, а класс функций, удовлетворяющих условию В, шире, чем класс функций, удовлетворяющих условию С. Условие А проверить трудно, а условие В или условие D проверить гораздо легче.

Если в какой-либо точке x,y G решение дифференциального уравнения не существует (через точку не проходит интегральная кривая), то в ней разрывна функция f x, y .

Если через какую-либо точку проходят две или более интегральных кривых, то функция f x, y непрерывна в этой точке, но ни одно из условий А, В, D не выполнено в ней.

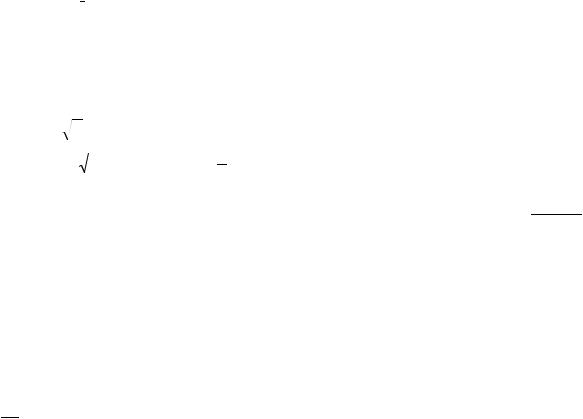
Пример. Найти общее и частное решение уравнения y y .

Очевидно, что общее решение будет y Cex . Так как правая часть непрерывна и удовлетворяет условию D, то через любую точку конечной плоскости OXY

проходит единственная интегральная кривая.
Для заданных начальных условий x0 , y0 G существует константа C0	y0 e x0 , такая что y0	C0ex0	( y0 e x0 )ex0 .

Понятие об особых точках и особых решениях дифференциального уравнения первого порядка.

Точка (x, y) называется не особой точкой дифференциального уравнения первого порядка y f x, y , если существует ее окрестность, что через каждую точкуэтой окрестности проходит единственная интегральная кривая.

Все прочие точки называются особыми точками дифференциального уравнения первого порядка y f x, y .

Особым решением называется решение, все точки (x, y) которого – особые.

Пример. y 3y 3

Решая это уравнение с разделяющимися переменными, получим общее решение y x C 3 и решение, не принадлежащее этому семейству – тривиальное

решение y 0 .

Каждая точка оси OX – особая, так как через нее проходят как тривиальное решение, так и частное решение из семейства y x C 3 .

y 0 - особое решение.

Пример. y

Заметим, что

y 0

. Общее решение

x C

, x C

(иначе

). Кроме того,

y 0

- тоже решение.

y 0

- особое решение.

f x, y

Заметим, что на особом решении не выполняются условия теоремы Коши, гарантирующие единственность. В самом деле, в том и другом примерах

терпят разрыв при y 0 .

Билет 11

Линейное уравнение.

y a x y b x

Существует два метода решения линейного уравнения: метод вариации произвольной постоянной и метод подстановки.

Метод вариации произвольной постоянной будет встречаться нам часто: при решении неоднородных линейных уравнений высшего порядка, при решении неоднородных систем линейных уравнений. Его надо знать твердо.

При решении методом вариации произвольной постоянной сначала решают однородное уравнение (с нулевой правой частью)

y a x y 0

Это – уравнение с разделяющимися переменными.

a x dx,

y Ce a x dx .

Затем варьируют произвольную постоянную, полагая C C x .

y C x e

a x dx

C x a x e

a x dx

Подставляем в неоднородное уравнение:

a x dx

Ca x

a x dx

Ca x e

b x

C e

При вариации произвольной постоянной здесь обязательно должны сократиться два члена, в этом идея метода.

C b x e a x dx ,

C x b x e a x dx dx C , где С – произвольная постоянная.

y x e

a x dx

b x e

a x dx

b x e

a x dx

Видно, что общее решение неоднородного уравнения равно сумме общего решения однородного уравнения и частного решения неоднородного уравнения. Это справедливо не только для линейных уравнений первого порядка, но и для линейных уравнений высших порядков, и для линейных систем. Там подобное утверждение называется теоремой о структуре общего решения неоднородного уравнения или системы.

Замечание. Решая уравнение методом вариации, обязательно приводите его к виду y a x y b x (если при	y стоит коэффициент, то делить на
него обязательно), иначе метод вариации даст ошибку.

При решении методом подстановки полагают

y x u x v x . Мы видели выше, что решение действительно является произведением двух функций от x. Этот факт здесь и используется. y u v uv . Подставляем в уравнение:

Теперь решают либо уравнение

u v uv a x uv b x .

u v a x uv 0 , определяя отсюда

u e a x dx , либо уравнение uv a x uv 0 , определяя отсюда

v e a x dx . Здесь при интегрировании не надо добавлять константу, она появится позже, при отыскании второй функции. В первом случае, остается найти

v из uv b x ,	v b x dx b x e a x dx dx C .
		u
Теперь y uv = e		a x dx		b x e	a x dx
Теперь y uv = e				b x e			C , как и выше.
								b x
			u v b x				u		dx
Во втором случае остается найти u из						,
								v
Теперь y uv = e		a x dx		b x e	a x dx
Теперь y uv = e				b x e			C , как и выше.

Пример. xy 2y 2x4 .

Решение методом вариации. Приводим уравнение, деля на коэффициент при y :

y 2 y	2x3 .
x
Решаем однородное уравнение y 2		y	,	dy	2 dx	, y Cx2 .
		x		y	x

a x dx

b x e dx C .

Варьируем произвольную постоянную

C C x ,

2Cx

C x

Подставляем в неоднородное уравнение C x2

2Cx 2Cx 2x3 ,

C 2x,

C x x2 C1 ,

y x2 x2 C1 .

Решение методом подстановки.

2uv 2x

y uv,

, xuv

2uv 0, xv

u v uv ,

x u v

dv 2 dx ,

v x2 ,

xu v 2x4 ,

x3u 2x4 ,

u 2x,

u x2 C

y uv x2 x2 C1 .

Билет 12

Формула Остроградского – Лиувилля.

Рассмотрим линейное однородное уравнение

a0 x y n a1 x y n 1 ... an 1 x y an x y 0 .

Определитель Вронского можно вычислить по формуле Остроградского – Лиувилля

W x Ce a0

x dx .

Вывод формулы Остроградского – Лиувилля.

Известна формула для производной определителя

a11 x

a12 x ...

a1n x

...

a11

a12 ...

a1n

d a21 x

a22 x ...

a2n x

...

a21

a22

a2n

dx ...

...

an1 x

an2 x ...

ann x

...

an1

an2

ann

...

y' ...

dW x

Вычислим

y1'

y2'

yn'

y1'

y2'

yn'

...+

dx ...

...

y n 1

n 1

y n 1

y1	y2 ...		yn		y1	...	yn
					y'	...	y'
'	'		'
y1	y2 ...		yn		1		n

...	...		...		...	...	...
				a1	y1n 1 ... an y1	... a1	ynn 1 ... an yn
n	n	...	n
y1	y2		yn	a0	a0	a0	a0

	y1	...
	y'	...
	1	...
0+...+0+	...	...
0+...+0+
a1	y n 1 ...
a0		1
a0

yn yn'

...

a1 ynn 1 a0

a1 W x . a0

dW x	a x		a1	x dx
W x	1	, W x Ce	a0	x .
W x	a0 x
Замечание. В формуле Остроградского – Лиувилля участвуют только коэффициенты при двух старших производных.
Рассмотрим частный случай уравнения второго порядка.
a0 x y a1 x y a2 x y 0 . Здесь формулу Остроградского – Лиувилля можно вывести проще. Рассмотрим					y1 x ,	y2 x - два

частных решения

a0 x y1 a1 x y1 a2 x y1 0 . , a0 x y2 a1 x y2 a2 x y2 0 . Умножим первое уравнение на y2 , а второе

на y1 и вычтем первое уравнение из второго.

a0 x y1 y2 y2 y1 a1 x y1 y2 y2 y1 0 .

y	y	y1 y2' y2 y1' , то W x y1' y2'
Так как W x y1'	y2'	y1 y2' y2 y1' , то W x y1' y2'			y1 y2''		y2' y1' y2 y1'' =	y1 y2'' y2 y1'' .
1	2		a0	x W x a1 x W x 0
			a0	x W x a1 x W x 0
Теперь уравнение можно переписать в виде						. Решая это уравнение с разделяющимися переменными, получаем
			a1	x
формулу Остроградского – Лиувилля W x Ce a0				x dx

Формула для построения второго частного решения по известному (построение фундаментальной системы).

W x

y y' y

Ce a0

x dx

2 1

x 0

Разделим обе части уравнения на

y y'

x dx

1 2

2 1

e a0

x .

C 1

Отсюда

e a0

x dx

dx C .

Нам

y2 y1 y12 e a0

x dx dx .

надо найти частное решение, поэтому выберем С=1, C 1=0, получим

Билет 13

Лекции 15–16. Линейные дифференциальные уравнения n –ого порядка с переменными коэффициентами.

Линейное однородное дифференциальное уравнение n –ого порядка с переменными коэффициентами может быть записано в виде

a0 x y n a1 x y n 1 ... an 1 x y an x y 0

Линейное неоднородное дифференциальное уравнение n –ого порядка с переменными коэффициентами может быть записано в виде

a0 x y n a1 x y n 1 ... an 1 x y an x y f x .

Если коэффициенты и правая часть – непрерывные функции и

a0 x 0 , то условия теоремы Коши выполнены, решения однородного и неоднородного

уравнений существуют и единственны.

Введем линейный дифференциальный оператор

p, x a

x d n

a x d n 1

... a

n 1

x d

x a

x pn ...a

n 1

x p a

x Здесь

dxn

dxn 1

p обозначает оператор дифференцирования

dx .

Ln p, x y 0 , а

линейное неоднородное – в виде Ln p, x y f x .

Тогда линейное однородное уравнение можно записать в виде

Так как Ln p, x линеен, то

Ln p, x y1 y2 Ln p, x y1 Ln p, x y2 ,

Ln p, x y Ln p, x y .

Пользуясь линейностью оператора, легко доказать теоремы о свойствах решений однородного и неоднородного уравнений (ниже обозначено yo - решение

однородного уравнения, yн - решение неоднородного уравнения).

Теоремы о свойствах решений.

1)сумма или разность решений однородного уравнения есть решение однородного уравнения,

2)разность решений неоднородного уравнения есть решение однородного уравнения,

3)сумма решений однородного и неоднородного уравнений есть решение неоднородного уравнения.

Докажем эти теоремы.

1)	L yo1 yo2 Lyo1 Lyo2	0
2)	L yн1 yн2 Lyн1 Lyн2	f x f x 0

3)L yo yн Lyo Lyн 0 f x f x .

Билет 14

Формула для построения второго частного решения по известному (построение фундаментальной системы).

W x

y y'

Ce a0

x dx .

x 0

Разделим обе части уравнения на

y y'

x dx

1 2

2 1

e a0

x .

				C 1	a1	x
		Отсюда	y2	C 1	e a0	x dx	dx C . Нам надо найти частное
			y	y2			1
			y	y2
			1	1					x
		решение, поэтому выберем С=1, C 1=0, получим y2 y1 y12						a1	x
		решение, поэтому выберем С=1, C 1=0, получим y2 y1 y12						e a0	x dx dx .
							1
		Билет 15
Линейная зависимость и независимость.
Функции g1 x , g2 x ,... gn x называются линейно независимыми, если
1 g1 x ... n gn x 0 1	0,... n	0	(допустима только тривиальная линейная комбинация функций, тождественно равная

нулю). В отличие от линейной независимости векторов здесь тождество линейной комбинации нулю, а не равенство. Это и понятно, так как равенство линейной комбинации нулю должно быть выполнено при любом значении аргумента.

	Функции g1 x , g2 x ,... gn x называются линейно зависимыми, если существует не нулевой набор констант (не все константы равны нулю)
,...		n	, такой что g	1	x ...	n	g	n	x 0	( 2	...	2	0) (существует нетривиальная линейная комбинация функций, тождественно
1		n	1	1		n		n		1		n

равная нулю).

Теорема. Для того чтобы функции были линейно зависимы, необходимо и достаточно, чтобы какая-либо из них линейно выражалась через остальные (представлялась в виде их линейной комбинации).

Докажите эту теорему самостоятельно, она доказывается так же, как аналогичная ей теорема о линейной зависимости векторов.

Определитель Вронского.

Определитель Вронского для функций y1 , y2 ,... yn вводится как определитель, столбцами которого являются производные этих функций от нулевого (сами функции) до n-1 го порядка.

1 / 21 2 > Следующая >>>

Соседние файлы в папке билеты

#
04.03.2014316.93 Кб71answers.pdf
#
04.03.20141.02 Mб183Ответы на билеты.doc
#
04.03.20143.66 Кб52Содержание OneNote.onetoc2