Основные динамические характеристики и законы поступательного и вращательного движений

Поступательное движение		Вращательное движение
Основные динамические характеристики
мера инертности - масса		мера инертности - момент инерции
причина движения - сила		причина движения - момент силы
количество движения - импульс		количество движения - момент импульса
Основное уравнение динамики
Основные энергетические характеристики
работа		работа
мощность		мощность
кинетическая энергия		кинетическая энергия

Пример 4.6.1. Платформа в виде диска радиусом и массой вращается по инерции около вертикальной оси с частотой . В центре платформы стоит человек массой . Какую линейную скорость относительно земли будет иметь человек, если перейдет на край платформы?

Р Дано: , , , . Ешение:

Платформа с человеком составляет замкнутую механическую систему, поэтому момент импульса этой системы должен иметь постоянное значение. Следовательно, , где и момент инерции и угловая скорость системы, когда человек стоит в центре платформы; и момент инерции и угловая скорость системы, когда человек стоит на краю платформы.

Момент инерции системы равен сумме момента инерции человека (считаем его материальной точкой) и момента инерции платформы. Поэтому (момент инерции человека в первом случае равен 0) и .

Учитывая, что , запишем закон сохранения момента импульса:

, откуда .

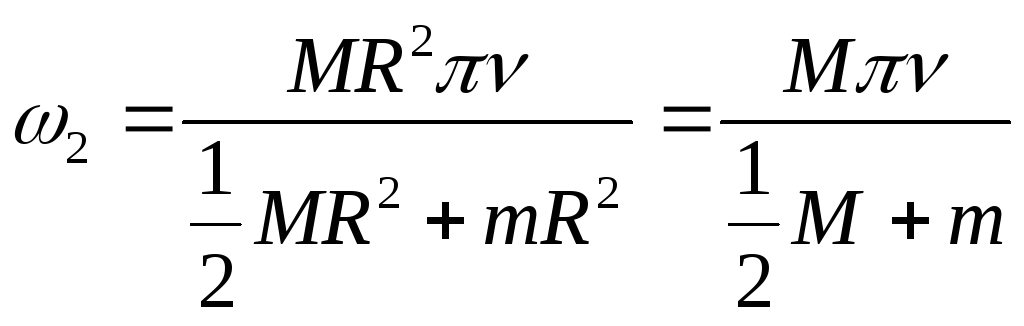Линейная скорость человека, стоящего на краю платформы, связана с угловой скоростью соотношением .

Таким образом,

Ответ: .

Пример 4.6.2. Маховик в виде диска массой и радиусом был раскручен до частоты и затем предоставлен самому себе. Вследствие трения маховик остановился. Найти момент сил трения, считая его постоянным, если маховик до полной остановки сделал 200 оборотов.

Р Дано: , , , . Ешение:

Применим формулу, выражающую связь работы диссипативной силы с изменением кинетической энергии: .

Работа при вращательном движении определяется по формуле , где момент силы трения относительно оси вращения, угловое перемещение (угол поворота) маховика.

Изменение кинетической энергии вращающегося тела , где , а . Поскольку, сделав 200 оборотов, маховик остановился, то .

Следовательно, .

Таким образом, .

Знак «минус» показывает, что момент силы трения оказывает тормозящее действие.

Ответ: .

Пример 4.6.3. Карандаш длиной , поставленный вертикально, падает на стол. Какую угловую и линейную скорости будет иметь в момент соприкосновения со столом: 1) середина карандаша, 2) верхний его конец? Считать, что нижний конец карандаша не проскальзывает.