5.5. Сложение взаимно перпендикулярных колебаний

1. Сложение взаимно перпендикулярных гармонических колебаний одинаковой частоты.

Пусть система одновременно участвует в двух гармонических колебаниях одинаковой частоты , происходящих во взаимно перпендикулярных направлениях Х и Y. Начало отсчета выберем так, чтобы начальная фаза первого колебания была равна нулю. Уравнения колебаний имеют вид:, где А и В – амплитуды складываемых колебаний, разность фаз складываемых колебаний.

Найдем уравнение траектории результирующего колебания , исключив параметр . Для этого представим уравнения колебаний в виде

.

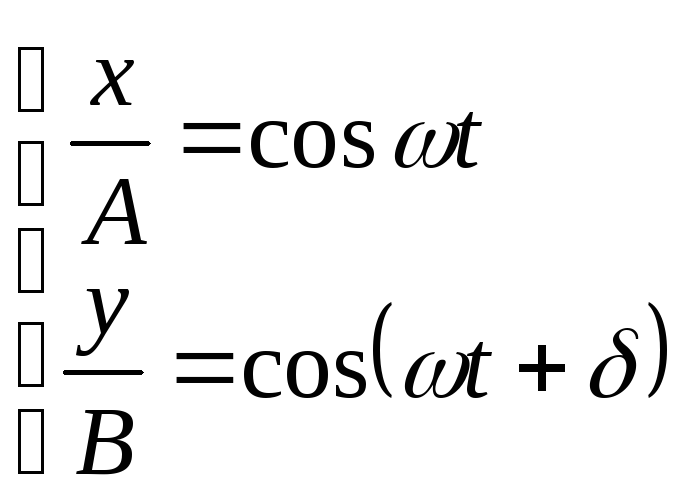Рассмотрим уравнение . Заменим на и . Получим .

Возведем в квадрат правую и левую часть уравнения:

. Заменим на и раскроем скобки: .

Приведем подобные члены: .

Учитывая, что , получим траекторию результирующего колебания: .

Траектория результирующего колебания имеет форму эллипса (такие колебания называются эллиптически поляризованными), оси которого ориентированы относительно осей координат произвольно.

Ориентация эллипса и его размеры зависят от амплитуд складываемых колебаний и их разности фаз. Проанализируем эти зависимости.

а) . Тогда и . Поэтому эллипс вырождается в отрезок прямой , где знак плюс соответствует нулю и чет-

ным значениям т (рис. 5.5.1, а), а знак минус – нечетным значениям т (рис. 5.5.1, б). Результирующее колебание является гармоническим колебанием с частотой и

амплитудой , совершающимся вдоль прямой, составляющей с осью Ох угол . Такие колебания называются линейно поляризованными.

б) . Тогда и . Поэтому уравнение траектории примет вид:

.

Это уравнение эллипса, оси которого совпадают с осями координат, а полуоси равны соответствующим амплитудам (рис. 5.5.2). Если , то эллипс вырожда-

ется в окружность. Такие колебания называются циркулярно поляризованными.

2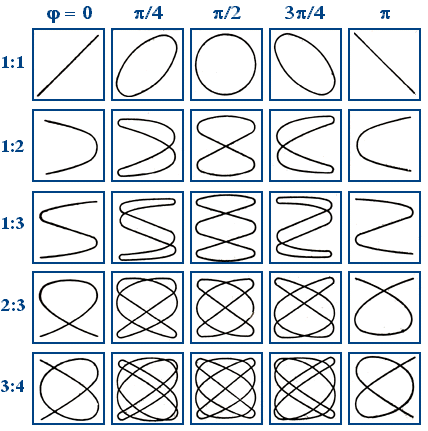. Сложение взаимно перпендикулярных гармонических колебаний различной частоты.

Е

Рис. 5.5.3. Фигуры Лиссажу

сли частоты складываемых взаимно перпендикулярных колебаний различны, то замкнутая траектория результирующего колебания имеет сложный вид и называется фигурой Лиссажу. Вид фигуры зависит от соотношения амплитуд, частот и разности фаз складываемых колебаний. На рис. 5.5.3 показаны некоторые фигуры Лиссажу для колебаний одинаковой амплитуды и различных отношений частот . Необходимо отметить, что отношение числа пересечений фигур Лиссажу с прямыми, параллельными осям координат, равно отношению частот складываемых колебаний.

Пример 5.5.1. Материальная точка участвует одновременно в двух взаимно перпендикулярных гармонических колебаниях, уравнения которых , см и , см. Определить траекторию точки. Построить траекторию с соблюдением масштаба.

Дано:

см,

с м.

Решение:

Исключим время из заданных уравнений. Представим второе уравнение в виде , см. Полученные выражения представляют собой уравнение параболы, ось которой совпадает с осью Х. Т.к. допустимые значения косинуса лежат в пределах от -1 до +1, то смещение точки по осям координат ограничено и заключено в пределах -1 до +1 см по оси Х и от -2 до +2 см по оси Y . Составим таблицу

х, см	-1	-0,75	-0,5	0	+0,5	+1
y, см	0	0,707	1	1,41	1,73	2

Выберем оси координат, нанесем масштаб и найдем точки, которые соединим плавной линией. Полученная кривая и есть траектория результирующего колебания (рис. 5.5.4).

Ответ: , см.