4.2. Методические указания к выполнению задания по теме 4

Средняя величина – это обобщающая количественная характеристика уровня варьирующего признака по однородной совокупности. Средние рассчитываются на основе массовых данных правильно статистически организованного массового наблюдения.

В зависимости от характера изучаемых явлений, от конкретных задач и целей статистического исследования применяются четыре вида средних:

– арифметическая;

– гармоническая;

– геометрическая;

– квадратическая.

Наиболее широкое применение и, следовательно, распространение имеет средняя арифметическая.

Средняя арифметическая может быть простой и взвешенной. Средняя арифметическая простая равна сумме произведений значений признака, деленной на их количество.

,

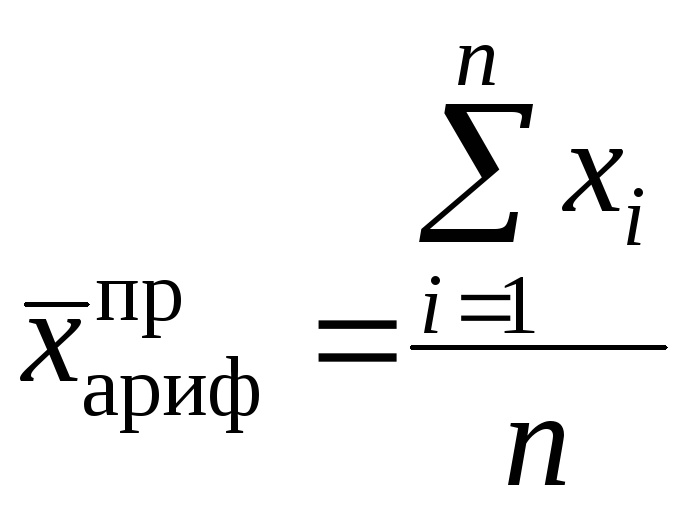где – значение признака у i-ой единицы совокупности; – число единиц наблюдения в исследуемой совокупности.

Пример. По данным табл. 4.1 определить среднюю заработную плату рабочего бригады.

Т а б л и ц а 4.1

Заработная плата рабочих цеха

Рабочие	Месячная заработная плата ( руб.)
1	15360
2	16840
3	16500
4	16840
5	16500
6	16840
ИТОГО:	98880

Для этого просуммируем зарплату всех рабочих (значение признака) и разделим на количество рабочих (число значений признака):

руб.

Если одно и то же значение признака встречается несколько раз, то рассчитывается средняя арифметическая взвешенная по формуле:

,

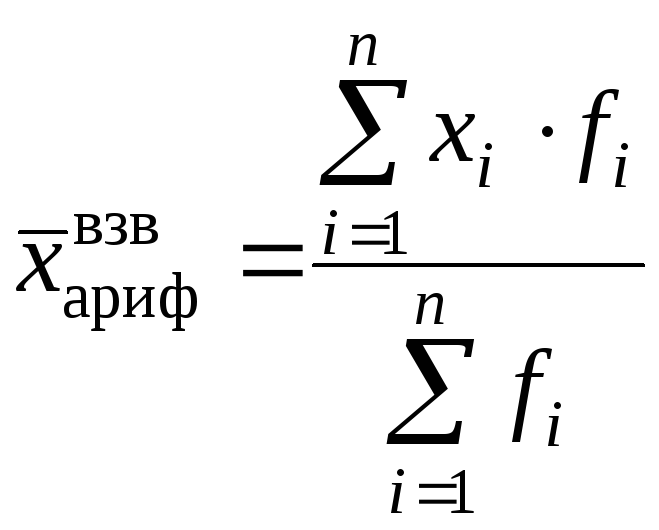где – частота, т. е. число случаев возникновения i-го значения признака.

Пример. По исходным данным, приведенным в табл. 4.1, построим вариационный ряд (см. табл. 4.2).

Т а б л и ц а 4.2

Пример расчета средней арифметической взвешенной в дискретном вариационном ряду

Месячная заработная плата (), руб.	Число рабочих ()
15360	1	15360
16500	2	33000
16840	3	50520
ИТОГО	6	98880

руб.

Средняя арифметическая обладает рядом свойств [2], позволяющих во многих случаях упростить ее расчет. Одним из таких упрощенных методов расчета является способ моментов:

,

где – значение признака имеющего максимальную частоту (условная средняя); – величины отклонения среднеарифметической от условной средней, которая определяется по формуле:

.

Пример. По исходным данным, приведенным в табл. 4.1, построим таблицу для вычисления средней арифметической методом моментов (табл. 4.3).

Т а б л и ц а 4.3

Пример расчета средней арифметической способом моментов

Месячная заработная плата (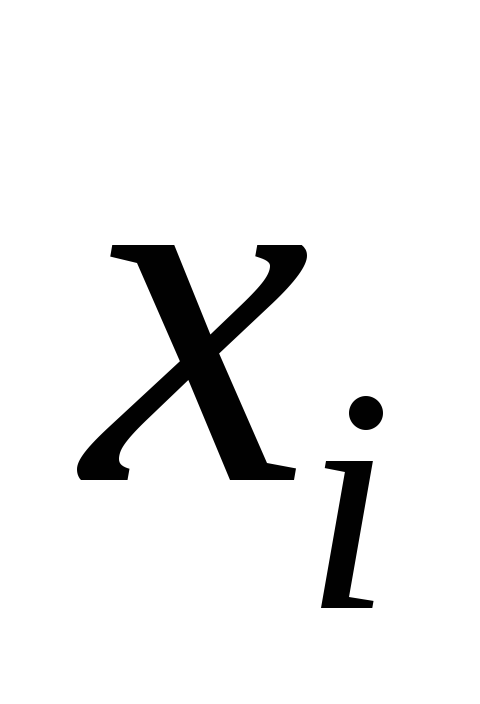), руб.	Число рабочих ()
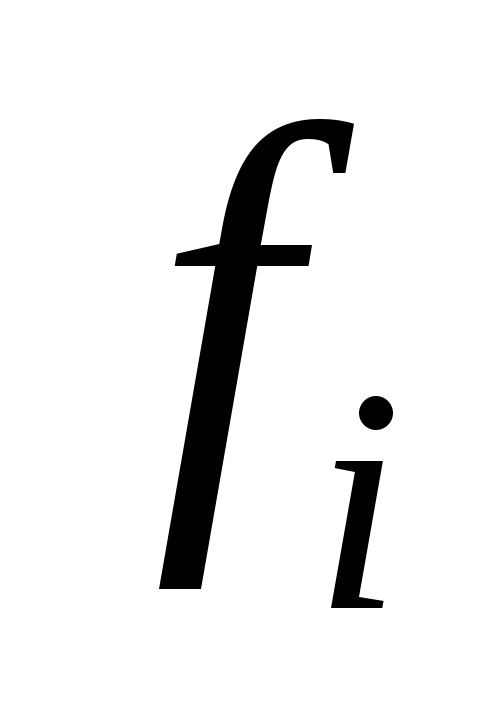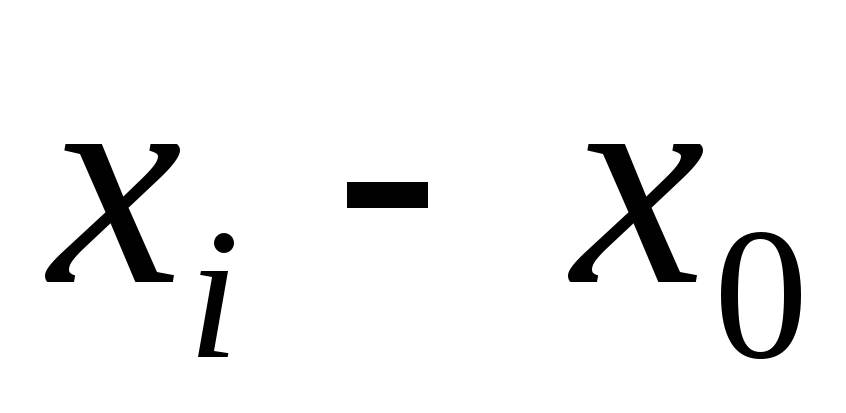
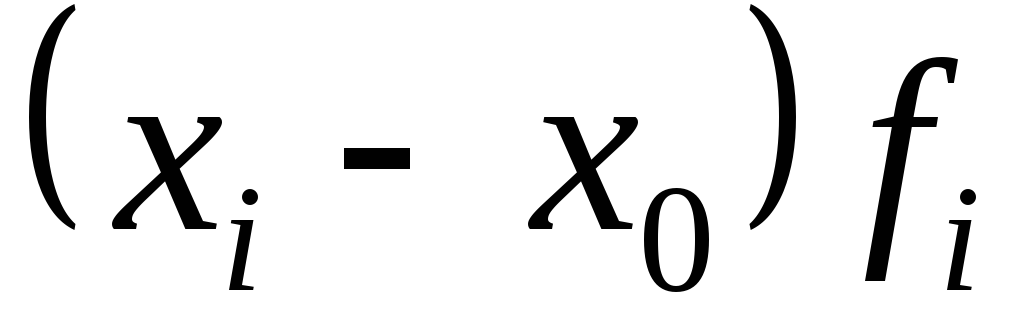
15360	1	–1480	–1480
16500	2	–340	–680
16840	3	0	0
ИТОГО	6		–2160

руб.

Средняя гармоническая простая вычисляется в случаях, когда средняя предназначается для расчета сумм слагаемых, обратно пропорциональных величине данного признака, т.е. когда суммированию подлежат сами варианты, а обратные им величины:

Средняя гармоническая простая рассчитывается по следующей формуле:

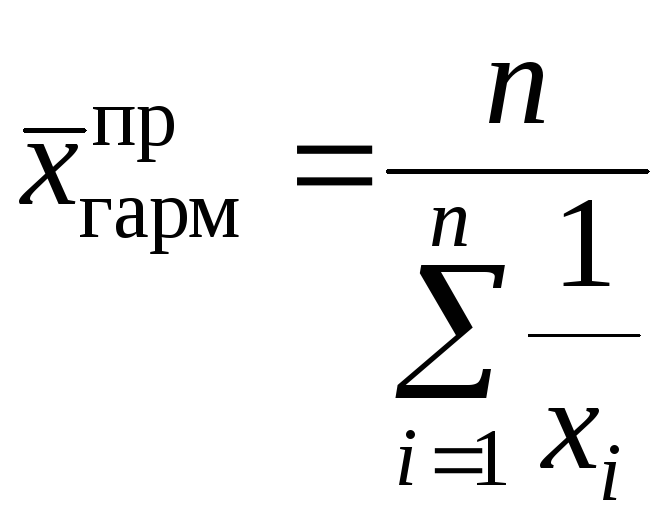
В тех случаях, когда статистическая информация не содержит частот по отдельным вариантам совокупности, а представлена как их произведение, применяется формула средней гармонической взвешенной:

.

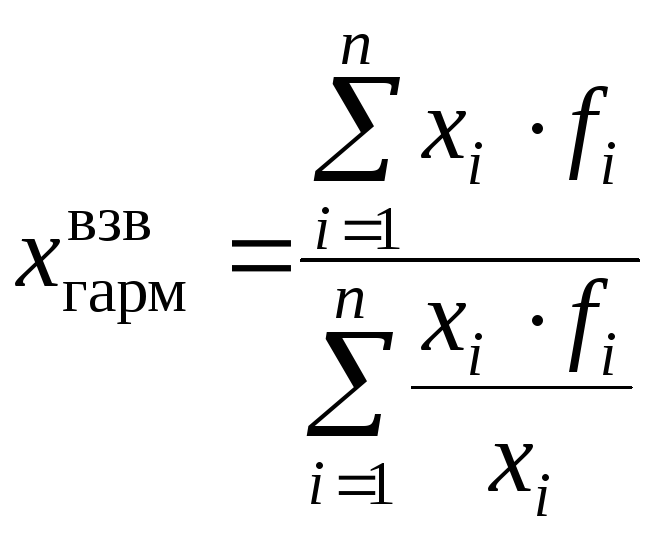Пример. По данным табл. 4.4 определить среднюю трудоемкость.

Т а б л и ц а 4.4