- •1.Задачи физической защиты информации
- •2.Физические поля как носители информации.
- •4.Закон полного тока в интегральной форме.
- •3.Эл. Магнитное поле.
- •5.Закон индукции Фарадея в интегральной форме.
- •6.Закон Гаусса в интегральной форме.
- •7.Закон непрерывности магнитной индукции в интегральной форме.
- •8.Силовые характеристики эл. Магнитного поля
- •9.Количественные характеристики эл. Магнитного поля.
- •12. Ротор векторного поля.
- •13. Закон полного тока в дифференциальной форме.
- •15. Закон Гаусса в дифференциальной форме.
- •19. Граничные условия для нормальной составляющей вектора смещения вблизи границы раздела сред.
- •20. Теорема единственности теории эл. Магнитного поля.
- •21. Скалярный и векторный потенциалы электромагнитного поля и условия калибровки Лоренса.
- •23. Запаздывающие потенциалы электромагнитного поля.
- •25. Поле ближней зоны и поля индукции электрического диполя.
- •26. Поле дальней зоны электрического диполя.
- •27. Поле плоской волны в однородной среде.
- •29. Коэффициент фазы. Коэффициент затухания плоской волны.
- •32. Классификация физических сред по электромагнитным свойствам.
- •33. Материальные уравнения электромагнитного поля.
- •34. Тензоры электрической, магнитной проницаемости, проводимости.
- •35. Система уравнений Максвелла электромагнитного поля.
- •36. Коэффициент Френеля.
- •37. Распространение волн в продольно неоднородной среде.
- •38. Рекуррентная процедура расчета полей в продольно неоднородной среде.
- •40. Закон полного прохождения плоской волны через границу раздела двух сред.
- •56. Уравнение Максвелла в комплексной формуле для sin-идальных полей.
- •53.51.50.48. Экранирование электрического поля с помощью производящего экрана
- •43,44 Волны в поперечно неоднородных средах
- •45,46,47 Эл маг поле в проводнике(релаксация)
- •59,60 Преобразования Фурье
- •54.55 Коэффициенты Френеля
5.Закон индукции Фарадея в интегральной форме.
Обобщенный закон электромагнитной индукции. Если рассматривать контур в однородном поле на который действует поверхности S. Обобщенный закон индукции устанавливает связь между эл. полем и магнитной индукцией. Переменное магнитное поле порождает эл. поле:
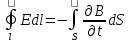
Если
поверхность S
неподвижна и контур l
неподвижен, то производную по времени
можно поменять в интеграле.
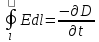 ;
;
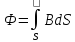 ;
;
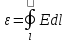 ;
;
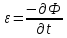 ;
;
Изменение тока магнитной индукции проходящего через незамкнутую поверхность взятую с обратным знаком пропорционально циркуляции электрического поля на замкнутом контуре L.
6.Закон Гаусса в интегральной форме.
Обобщенный закон Гаусса связывает между собой вектор смещения и заряды.
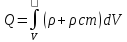 -
полный
заряд. Полный заряд может характеризоваться
так же: Q=
-
полный
заряд. Полный заряд может характеризоваться
так же: Q=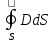
Поток вектора смещения электрической индукции через замкнутую поверхность S пропорционально величине свободного заряда, находящегося в объеме V.
7.Закон непрерывности магнитной индукции в интегральной форме.
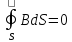 D=r0*D
D=r0*D
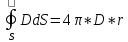 2
D=
2
D=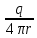 2
D=
2
D=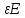 E=r0
E=r0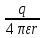 2
F=
2
F=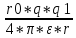 2
2
Поток магнитной индукции через замкнутую поверхность равен нулю. В природе существуют только эл. заряды, но нет магнитных.
8.Силовые характеристики эл. Магнитного поля
E
напряженность эл. поля – векторная
величина , характеризующая эл. поле в
данной точке и численно равная отношению
силы F
действующей на заряд помещенный в
данную точку поля к величине этого
заряда q.
E=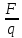 Вектор У выражается как градиент
потенциала взятый с обратным знаком.
Вектор У выражается как градиент
потенциала взятый с обратным знаком.
E=-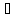 φ
Er=-
φ
Er=-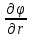 =-
=-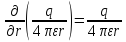 2
2
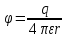
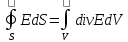 =
=
B
магнитная индукция – векторная величина,
являющейся силовой характеристикой
магнитного поля в данной точке
пространства. Показывает с какой силой
F
магнитного поля действует на заряд q,
движущийся со скоростью v.
F=q[v*B];
q=q*v*B*sin(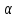 )
)
9.Количественные характеристики эл. Магнитного поля.
Напряженность магнитного поля – это векторная функция, величина которой равна разности вектора магнитной индукции и вектора намагниченности.
H=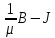 эта характеристика не зависит от
магнитных свойств среды в вакууме и
совпадает с B.
В среде определяет вклад внешних
относительно к среде источников поля.
эта характеристика не зависит от
магнитных свойств среды в вакууме и
совпадает с B.
В среде определяет вклад внешних
относительно к среде источников поля.
D
– электрическая индукция, векторная
величина равная сумме вектора напряженноси
эл. поля и вектора поляризации. D=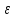 0E+P
Эта характеристика не определяет
электрическое состояние вещества в
эл. поле. Вектор смещения характеризует
поляризацию среды в некоторой точке,
может зависеть от значения эл. поля в
некоторой точке может зависеть от
значения эл. поля в некоторой окрестности
этой точки.
0E+P
Эта характеристика не определяет
электрическое состояние вещества в
эл. поле. Вектор смещения характеризует
поляризацию среды в некоторой точке,
может зависеть от значения эл. поля в
некоторой точке может зависеть от
значения эл. поля в некоторой окрестности
этой точки.
10. Градиент скалярного поля
Рассмотрим электростатическое поле. Работа по перемещению заряда из данной точки поля в бесконечность называется потенциалом электростатического поля.
Поле создаваемое любой совокупностью зарядов в ограниченном объеме спадает до нуля в бесконечно удаленной точке.
Пусть задано скалярное поле U=f(x,y,z).
∆r=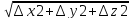 -
-
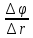 =(E*r0)
=(E*r0)
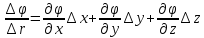

r0 – единичный вектор направления
Градиентом скалярной функции называется вектор направленный в сторону max ее возрастания и по величине равный скорости возрастания
11. Дивергенция векторного поля.
Дивергенцией
векторного поля или расходимостью
называется скалярная функция, определяемая
равенством: div
a(M)=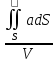 ; div
a(M)=
; div
a(M)=
Векторное поле a(м) порождает скалярное поле diva(м). Поток векторного поля через замкнутую называется SS в направлении внешней нормали равен тройному интегралу от дивергенции векторного поля по области ограниченной этой поверхностью.
div
a(м) есть предел отношения потока поля
a(м) через бесконечно малую замкнутую
поверхность, окружающую точку M, к
величине объема ограниченного этой
поверхностью. Дивергенция зависит от
вектора систем координат. С помощью
вектора –- тела div
a(M)=(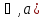 =
=