8. Цепні та базисні величини.

Относительные величины базисные – результат сравнения абсолютных величин за ряд последовательных периодов времени с данными базового периода.

Цепные относительные величины – результат сравнения абсолютных величин за текущий период времени с данными предыдущего периода.

Наиболее распространенными относительными величинами динамики являются коэффициент роста, темп прироста.

9. Дисперсія. Формули її обчислення. Математичні властивості дисперсії.

Дисперсия случайной величины́ — мера разброса данной случайной величины, то есть её отклонения от математического ожидания. Обозначается D[X] в русской литературе и varX (англ. variance) в зарубежной. В статистике часто употребляется обозначение или . Квадратный корень из дисперсии, равный σ , называется среднеквадратичным отклонением, стандартным отклонением или стандартным разбросом. Стандартное отклонение измеряется в тех же единицах, что и сама случайная величина, а дисперсия измеряется в квадратах этой единицы измерения.

Пусть — случайная величина, определённая на некотором вероятностном пространстве. Тогда ,где символ M обозначает математическое ожидание.

• Дисперсия любой случайной величины неотрицательна:

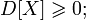
• Если дисперсия случайной величины конечна, то конечно и её математическое ожидание;

• Если случайная величина равна константе, то её дисперсия равна нулю: D[a] = 0. Верно и обратное: если D[X] = 0, то X = M[X] почти всюду;

• Дисперсия суммы двух случайных величин равна: 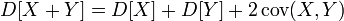, где 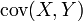— их ковариация;

• 

• 

• 

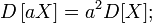
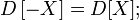
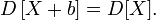
10. Суть середньої величини у статистиці. Формули середніх величин.

Средняя величина – это обобщающая количественная характеристика совокупности по изучаемому признаку в конкретных условиях места и времени. Средняя величина отражает то общее и типичное, что присуще единицам данной совокупности

Введем следующие условные обозначения:

- величины, для которых исчисляется средняя;

- средняя, где черта сверху свидетельствует о том, что имеет место осреднение индивидуальных значений;

f- частота (повторяемость индивидуальных значений признака).

Различные средние выводятся из общей формулы степенной средней:

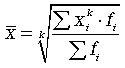
при k = 1 - средняя арифметическая; k = -1 - средняя гармоническая; k = 0 - средняя геометрическая; k = -2 - средняя квадратическая.

11. Середнє арифметичне та його властивості.

Найбільш поширеним видом середніх величин в статистиці є середня арифметична. Вона застосовується у формі простої середньої і зваженої середньої.

Середня арифметична проста застосовується в тих випадках, коли всі варіанти зустрічаються один раз, або мають однакові частоти в досліджуваній сукупності. її отримують шляхом додавання окремих варіантів і діленням суми на число доданків.

Можна сказати, що середня арифметична величина - середнє складова. При її обчисленні загальний обсяг ознаки подумки розподіляється порівну між усіма одиницями сукупності.

Розрізняють 2 види арифметичних середніх:

• Невиважену (просту);

• Виважену.

Середня арифметична невиважена розраховується для несгруппірованних даних за формулою: .

Для масових статистичних сукупностей розраховується зважена середня арифметична за формулою: .

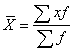Якщо при угруповання значення осередненою ознаки задані інтервалами, то при розрахунку середньої арифметичної величини як значення ознаки в групах беруть середини цих інтервалів, тобто виходять з гіпотези про рівномірний розподіл одиниць сукупності по інтервалу значень ознаки. Для відкритих інтервалів в першій і останній групі, якщо такі є, значення ознаки треба визначити експертним шляхом виходячи із сутності, властивостей ознаки і сукупності.