§4. Расстояние от точки до плоскости в пространстве

Пусть в пространстве Oxyz плоскость задана уравнением

,. (10)

г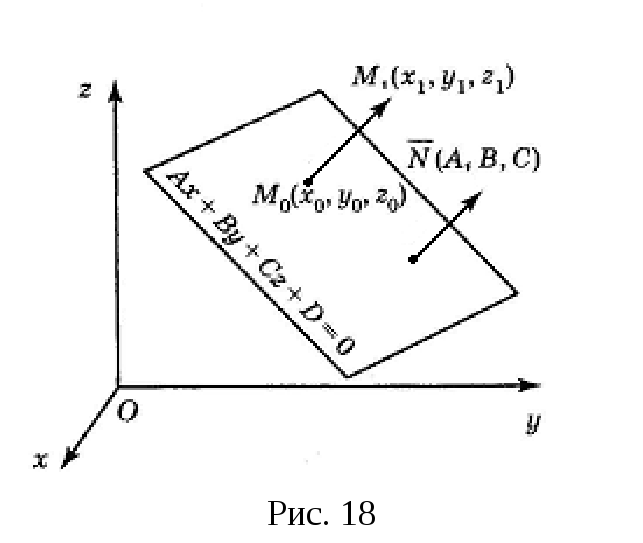де A, B, C, D – известные числа. Дана точка , ее координаты – заданные числа. Нужно найти d – расстояние от точки до плоскости с уравнением (10). Нормальный вектор этой плоскости равен

Пусть – основание перпендикуляра, опущенного из точки на заданную плоскость (рис. 18). Ясно, что длина вектора равна искомому расстоянию d. Ясно также, что вектор коллинеарен . Проекции вектора на оси координат равны разностям координат конца и начала:

Скалярное произведение этого вектора и вектора определим по формуле (17) главы 1:

. (11)

С другой стороны, скалярное произведение в левой части (11) равно

. (12)

Здесь берётся, когда угол , и , когда этот угол равен Выражение (12) подставим в левую часть формулы (11), а в правой части раскроем скобки. Получим

. (13)

Точка лежит на плоскости с уравнением (10), поэтому её координаты удовлетворяют (10), т. е. имеет место соотношение . Значит, Теперь формулу (13) можно записать так: . Найдем теперь , учитывая, что :

. (14)

Из формулы (14) видно, что для нахождения расстояния от точки до плоскости с уравнением (10) нужно в левую часть уравнения (10) вместо поставить координаты заданной точки , а затем найденное число поделить на . Полученное число будет равно , если оно положительное, и если это число отрицательное. Тем самым найдём искомое расстояние .

§5. Прямая в пространстве и ее уравнения

Общие уравнения прямой в пространстве. Пусть в пространстве Oxyz две плоскости заданы уравнениями

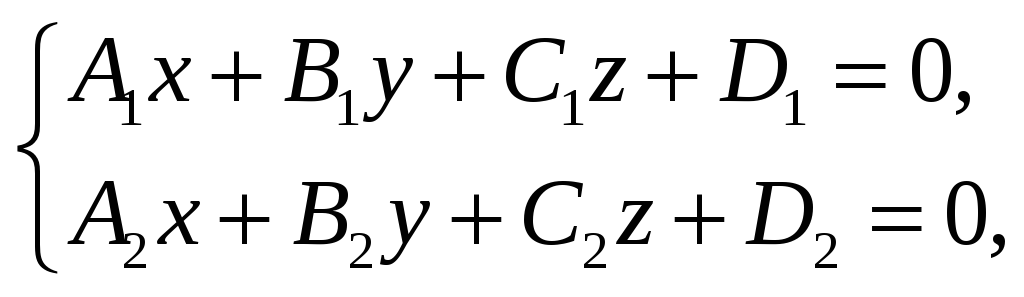(15)

где – известные числа. Пусть эти плоскости не параллельны (не выполняется условие параллельности плоскостей), тогда они пересекаются по прямой. Уравнения в системе (15) являются уравнениями этой прямой. Их называют общими уравнениями прямой в пространстве.

Векторное уравнение прямой. Параметрические уравнения прямой. Пусть в системе Oxyz прямая определена следующим образом:

• заданы координаты точки , лежащей на прямой;

• заданы проекции ненулевого вектора , параллельного прямой ( называется направляющим вектором прямой).

Пусть – произвольная точка рассматриваемой прямой и , – радиусы-векторы точек , . Из рис. 19 видно, что

. (16)

Так как вектор коллинеарен , то ясно, что можно получить умножением на некоторый скалярный множитель . Тогда

. (17)

Отсюда , вектор направлен, как , при , и в противоположную сторону при . Запишем (16) с учётом (17) в виде

. (18)

Это соотношение называется векторным уравнением рассматриваемой прямой, а скалярная величина – параметром. Каждому значению согласно (18) отвечает вектор , конец которого лежит на прямой. При изменении этот вектор изменяется, его конец – точка – движется по прямой. Мы учли, что , –заданные постоянные векторы, причём проекции вектора на оси координат равны координатам точки , так как есть радиус-вектор этой точки, т. е. в (18) . Поскольку есть радиус-вектор точки его проекции равны координатам точки т. е. .

Как известно, при умножении вектора на число умножаются на это число все проекции вектора на оси координат, поэтому . При сложении векторов их проекции складываются, поэтому , но согласно (18) этот вектор равен , следовательно, равны соответствующие проекции:

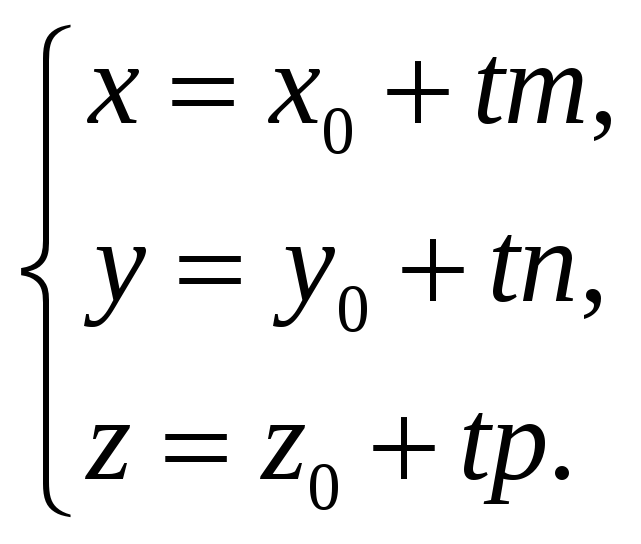(19)

Эти соотношения называют параметрическими уравнениями рассматриваемой прямой. Каждому значению параметра на прямой отвечает определённая точка координаты которой вычисляются по формуле (19). При изменении точка с указанными координатами движется по прямой, и её координаты изменяются согласно (19).