§15. Парабола

Параболой называется геометрическое место точек на плоскости, равноудалённых от заданной точки, называемой фокусом, и заданной прямой, называемой директрисой. Пусть – фокус. Ось Ox проведём через перпендикулярно директрисе (рис. 26).

П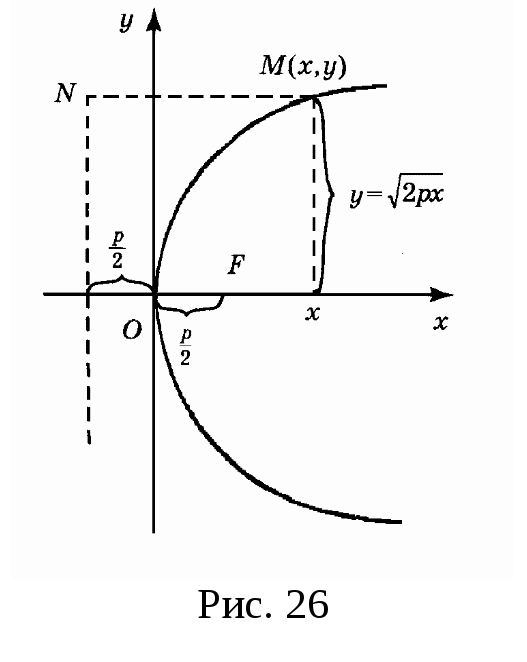усть – расстояние от фокуса до директрисы. Это число задано и называется параметром параболы. Начало координат возьмём в середине перпендикуляра, опущенного из точки на директрису. Тогда фокус будет иметь координаты . Директриса имеет уравнение . Пусть – произвольная точка параболы, – основание перпендикуляра, опущенного из точки на директрису. Из рис. 26 видно, что расстояние

. (45)

Запишем расстояние от до :

(46)

Для любой точки параболы имеем (по определению). Подставим сюда выражения (45), (46) и получим уравнение параболы

.

Упростим его, избавляясь от корня. Получим каноническое уравнение параболы

. (47)

И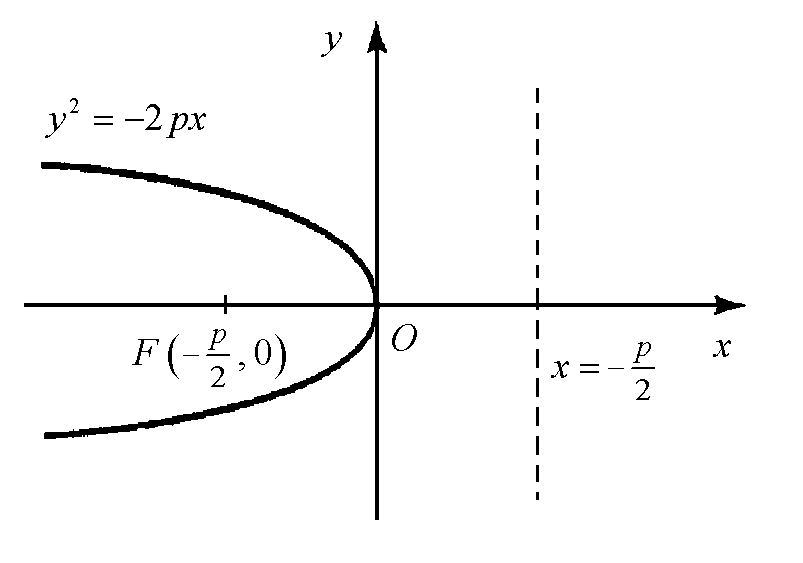сследуем форму параболы по уравнению (47). Так как это уравнение содержит только во второй степени, то, как и в случае эллипса, Ox является осью симметрии параболы. Следовательно, вид параболы достаточно установить в верхней полуплоскости, где . Для таких значений уравнение (47) запишем в виде . Эта формула выражает ординату точки , абсцисса которой равна . Когда , согласно последней формуле , точка совпадает с . С увеличением – абсциссы точки – её ордината, равная , неограниченно растёт, и точка уходит вверх и вправо. В силу симметрии остальная часть параболы вычерчивается сразу. Если Ox провести от к директрисе, то получим параболу, изображенную на рис. 27. Легко проверить, что уравнение параболы в этом случае будет иметь вид Пусть теперь ось Oy направлена п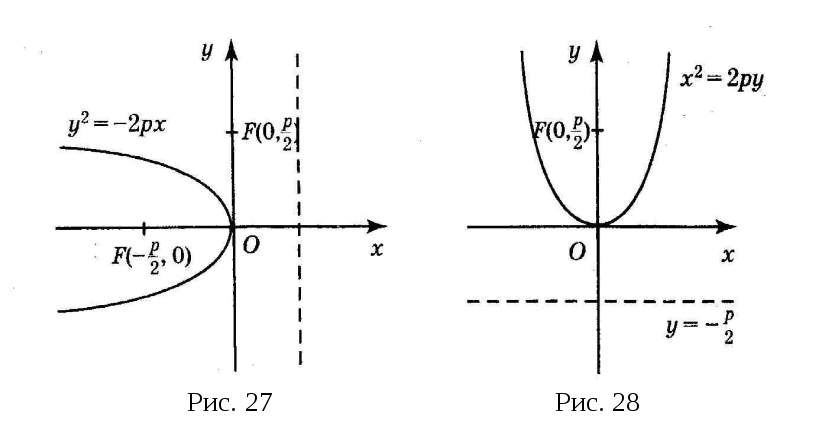ерпендикулярно к директрисе и проходит через . При этом уравнение параболы будет иметь вид (см. рис. 28).

§16. Преобразование координат на плоскости

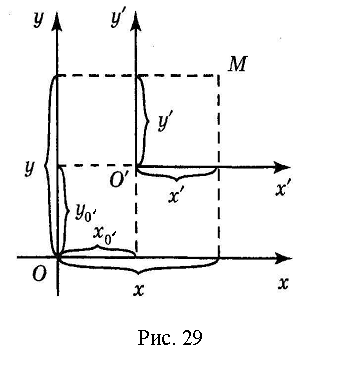
Параллельный перенос осей координат. Пусть – исходная система координат, – новая система координат, полученная параллельным переносом исходной системы, как показано на рис. 29. Положение новой системы по отношению к старой определим, задав координаты нового начала в старой системе координат, где – заданные числа. Пусть , – координаты точки в новой системе, – координаты точки в исходной системе. Как видно из рис. 29, , . Итак,

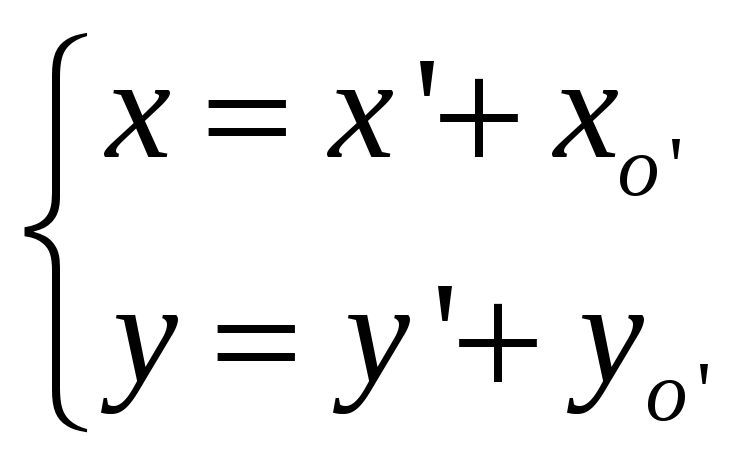(48)

Эти формулы выражают старые координаты точки через её новые координаты.

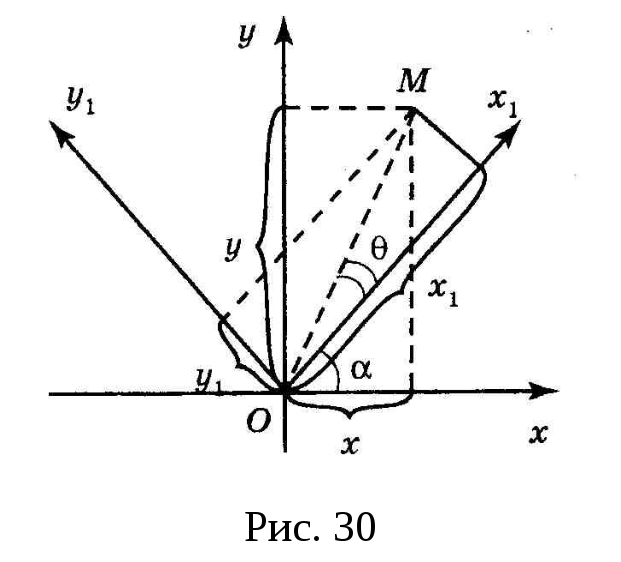
Поворот осей координат. Пусть – исходная система координат, а новая система координат получена поворотом исходной вокруг начала координат на угол , где  – заданное число (см. рис. 30). Угол берётся со знаком «+», если отсчёт ведётся против хода часовой стрелки от оси Ox. Пусть – координаты точки в системе , – координаты точки в системе . Пусть и – угол, образованный отрезком с осью , причём, как и этот угол берётся со знаком «+», если отсчёт ведётся от оси против хода часовой стрелки. Из рис. 30 видно, что

(49)

С другой стороны,

(50)

Формулы (50) перепишем, использовав известные формулы тригонометрии для косинуса и синуса суммы: С учётом (49) запишем

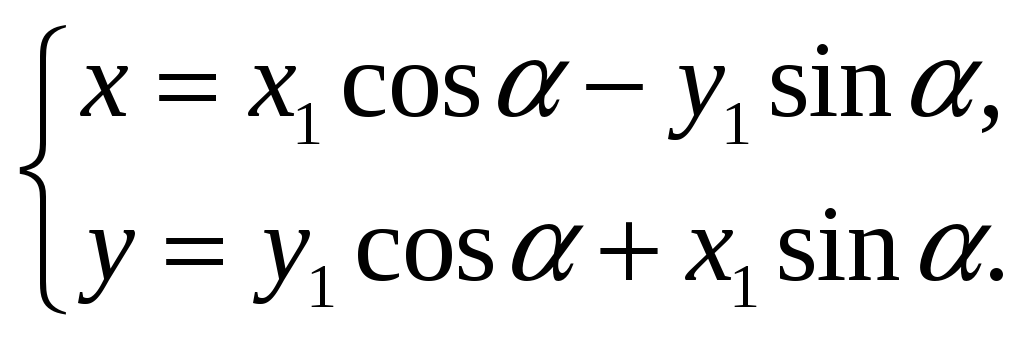(51)

Эти формулы выражают старые координаты точки через её новые координаты в случае поворота осей координат.

Общий случай. Пусть – исходная система координат, – новая система координат (рис. 31). Положение новой системы по отношению к старой определим, задав:

• координаты 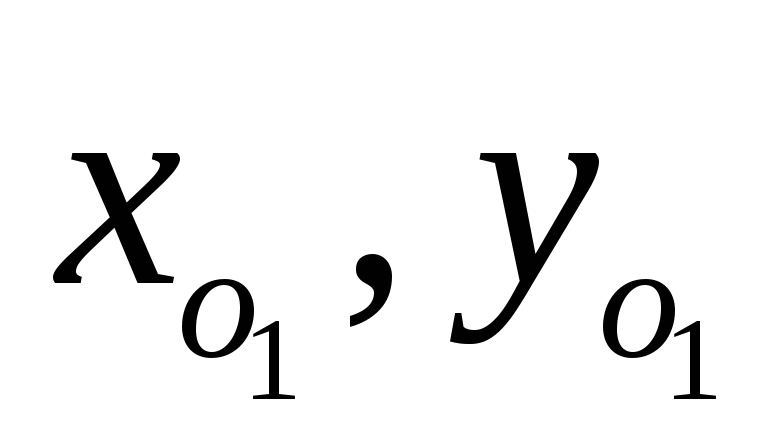нового начала 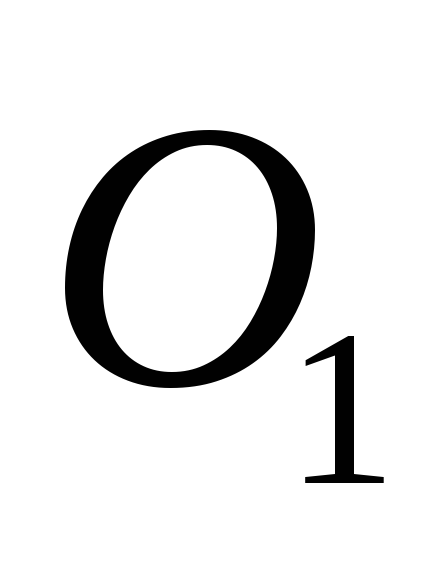в старой системе координат;

• угол который образует ось 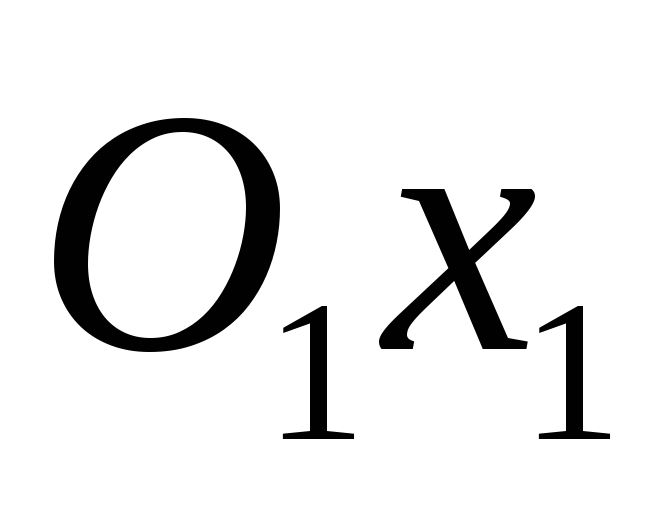с Ox.

П

Рис. 31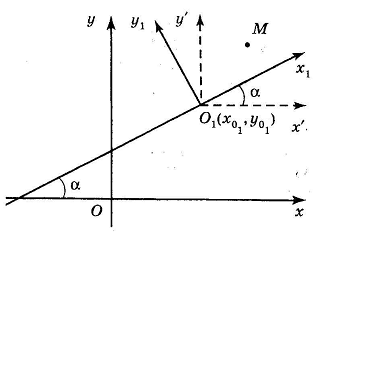

усть – координаты точки в старой системе, а – координаты точки в новой системе. Нужно найти связь между ними. С этой целью введём вспомогательную систему координат , полученную параллельным переносом старой системы Пусть , – координаты точки в этой вспомогательной системе. Так как новая система координат получена поворотом вспомогательной системы на угол то координаты , точки через координаты этой точки выражаются формулами (51), в которых нужно заменить на , :

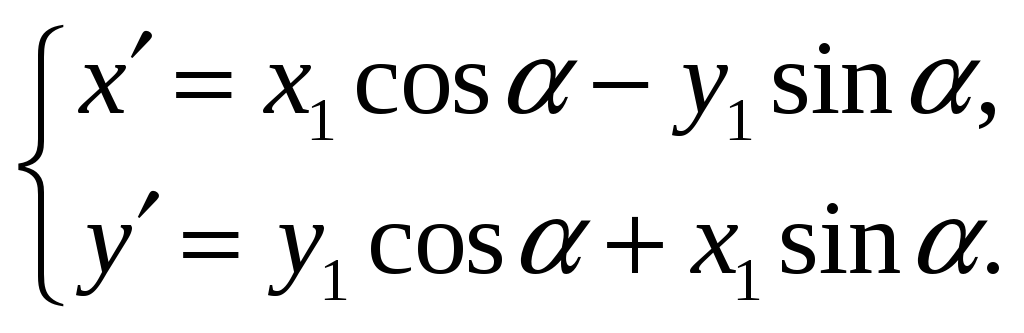(52)

Так как система координат получена параллельным переносом , то координаты точки в исходной системе выражаются через координаты , по формулам (48), в которых нужно заменить на : В эти формулы вместо , подставим (52) и получим

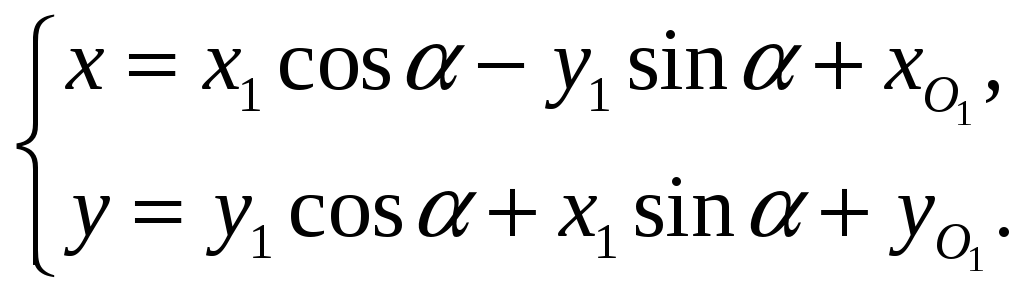(53)

Эти формулы выражают старые координаты точки через её новые координаты в новой системе.

Преобразования координат на плоскости применяются, в частности, для упрощения вида уравнений кривых. В системе координат возьмём, например, эллипс с каноническим уравнением

(54)

Подставим вместо их выражения (53) через , тем самым получим уравнение эллипса в новой системе координат . Это будет уравнение общего вида (после раскрытия скобок)

.

Таким образом, перейдя к системе , от канонического уравнения (54) эллипса мы перешли к более сложному уравнению – уравнению второй степени общего вида. Можно показать, что, наоборот, от последнего уравнения в системе , подобрав другую систему координат можно получить каноническое уравнение, определяющее либо окружность, либо эллипс, либо параболу, либо гиперболу, либо пару прямых, как, например, уравнение (, ), если не имеет место случай, когда уравнение определяет лишь точку или ничего не определяет.