
- •§1. Действительные числа, числовая ось, определители …
- •Глава 1. Элементы векторной алгебры
- •§1. Действительные числа, числовая ось, определители второго и третьего порядков
- •§2. Декартовы координаты. Полярные координаты
- •§3. Векторы, линейные операции над ними
- •§4. Проекция вектора на ось
- •§5. Разложение вектора по базисным векторам
- •§6. Линейные операции над векторами, заданными своими проекциями
- •§7. Длина вектора. Расстояние между двумя точками
- •§8. Направляющие косинусы вектора
- •§9. Скалярное произведение векторов, угол между
- •§10. Векторное произведение векторов, условие коллинеарности двух векторов, площадь треугольника
- •§11. Смешанное произведение векторов и его геометрический смысл. Условие компланарности трех векторов
- •Глава 2. Элементы аналитической геометрии
- •§1. Уравнение поверхности и уравнения линии в пространстве
- •§2. Плоскость, общее уравнение плоскости
- •§3. Угол между двумя плоскостями, условия параллельности и перпендикулярности плоскостей
- •§4. Расстояние от точки до плоскости в пространстве
- •§5. Прямая в пространстве и ее уравнения
- •§6. Канонические уравнения прямой. Уравнения прямой, проходящей через две заданные точки
- •§7. Угол между двумя прямыми, условия параллельности и перпендикулярности
- •§8. Уравнение линии на плоскости
- •§9. Общее уравнение прямой на плоскости, угол между прямыми
- •§10. Уравнение прямой с угловым коэффициентом,
- •§11. Уравнение прямой, проходящей через заданную точку с заданным угловым коэффициентом. Уравнение прямой, проходящей через две заданные точки
- •§12. Кривые второго порядка. Окружность
- •§13. Эллипс
- •§14. Гипербола
- •§15. Парабола
- •§16. Преобразование координат на плоскости
- •§17. Понятие о многомерном евклидовом пространстве
- •§18. Поверхности второго порядка. Сфера. Цилиндр
- •§19. Эллипсоид
- •§21. Однополостный и двуполостный гиперболоиды
- •§22. Эллиптический и гиперболический параболоиды
- •Глава 3. Элементы линейной алгебры
- •§1. Определители высших порядков
- •§2. Свойства определителей
- •§3. Матрицы и действия над ними. Обратная матрица
- •§4. Системы линейных алгебраических уравнений с неизвестными. Матричный метод решения
- •§5. Формулы Крамера
- •§6. Общая система линейных алгебраических уравнений. Метод Гаусса
- •§7. Ранг матрицы. Теорема Кронекера – Капелли
- •§8. Однородные системы
§2. Плоскость, общее уравнение плоскости
Пусть в пространстве Oxyz задана плоскость, т. е. заданы:
-
координаты
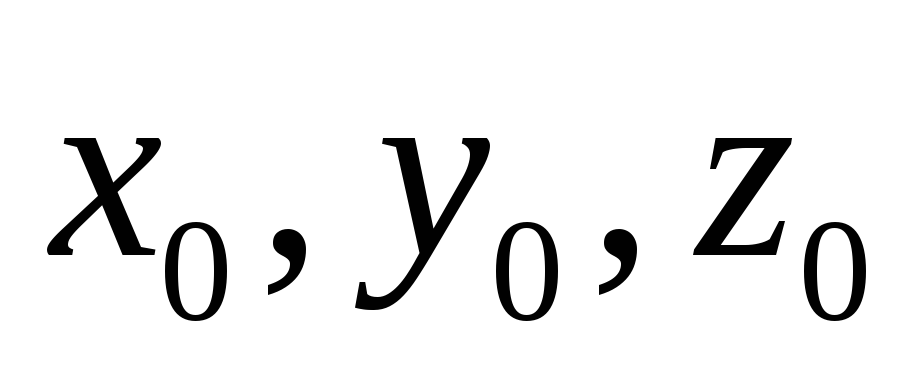 точки
точки
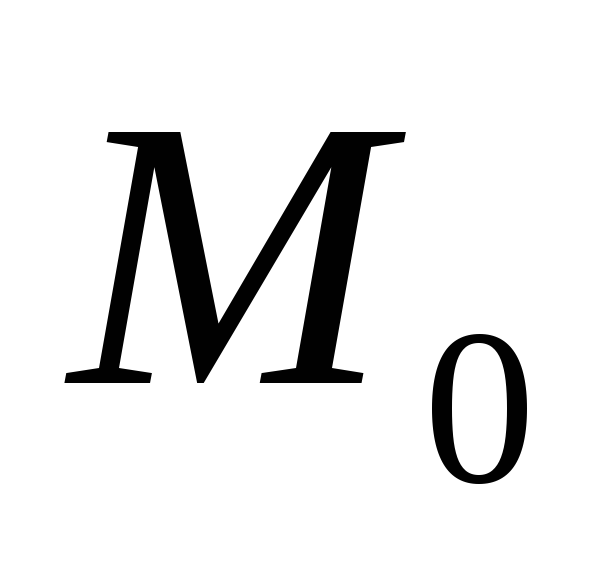 ,
лежащей на этой плоскости;
,
лежащей на этой плоскости; -
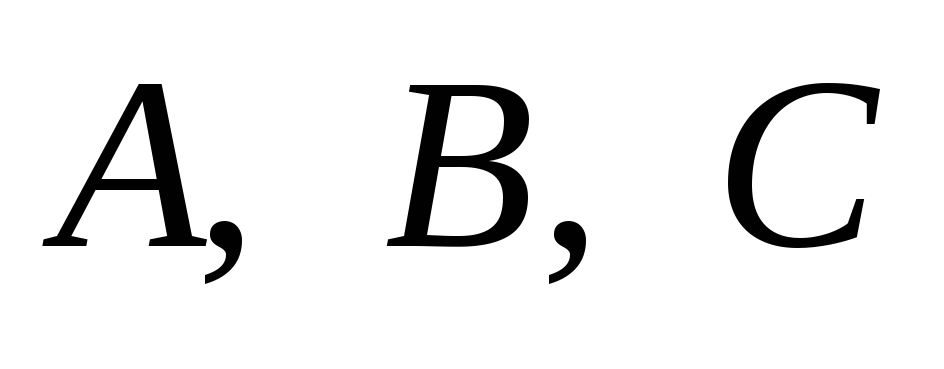 – проекции на
оси координат ненулевого вектора
– проекции на
оси координат ненулевого вектора
 ,
перпендикулярного плоскости, который
называется нормальным
вектором плоскости.
,
перпендикулярного плоскости, который
называется нормальным
вектором плоскости.
П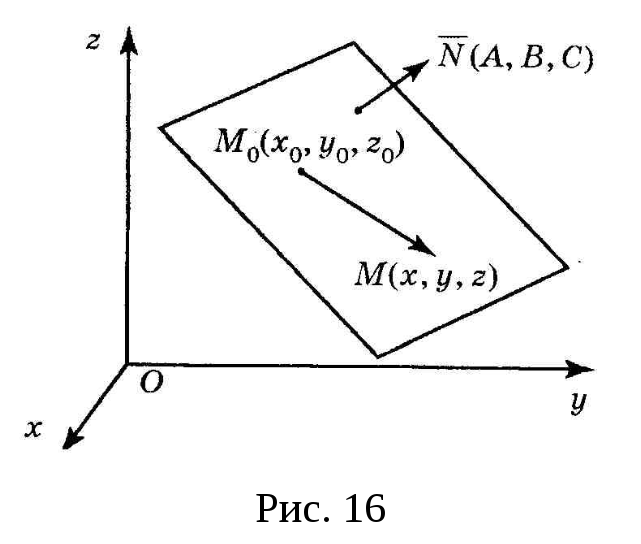 усть
усть
![]() – произвольная точка плоскости.
Рассмотрим вектор
– произвольная точка плоскости.
Рассмотрим вектор
![]() (см. рис. 16). Он лежит на рассматриваемой
плоскости и поэтому перпендикулярен
нормальному вектору
(см. рис. 16). Он лежит на рассматриваемой
плоскости и поэтому перпендикулярен
нормальному вектору
![]() этой плоскости, следовательно, скалярное
произведение этих векторов
этой плоскости, следовательно, скалярное
произведение этих векторов
![]() .
Выразим скалярное произведение через
проекции векторов. Получим
.
Выразим скалярное произведение через
проекции векторов. Получим
![]() . (4)
. (4)
Это есть уравнение
рассматриваемой плоскости, Здесь
![]() – текущие координаты, т. е. координаты
произвольной точки плоскости.
– текущие координаты, т. е. координаты
произвольной точки плоскости.
Общее уравнение
плоскости. Возьмём
уравнение первой степени относительно
![]() :
:
![]() , (5)
, (5)
где A,
B,
C,
D
– заданные числа. Будем считать, что
A,
B,
C
одновременно не обращаются в нуль. Если
же эти числа обращаются в нуль
одновременно, то (5) примет вид
![]() и уже не будет уравнением. Пусть
и уже не будет уравнением. Пусть
![]() ,
тогда (5) можно записать в виде
,
тогда (5) можно записать в виде
![]() .
(6)
.
(6)
Но это есть
уравнение вида (4), поэтому оно
(следовательно, и уравнение (5)) определяет
в пространстве Oxyz
плоскость, проходящую через точку
![]() и перпендикулярную к вектору
и перпендикулярную к вектору
![]() .
.
Итак, уравнение
(5) в пространстве всегда определяет
плоскость с нормальным вектором
![]() .
Оно называется общим
уравнением плоскости.
Мы показали также, что в (5) числа
.
Оно называется общим
уравнением плоскости.
Мы показали также, что в (5) числа
![]() (коэффициенты уравнения при текущих
координатах) представляют собой проекции
на оси координат нормального вектора
(коэффициенты уравнения при текущих
координатах) представляют собой проекции
на оси координат нормального вектора
![]() этой плоскости. Отметим отдельные
частные случаи уравнения (5).
этой плоскости. Отметим отдельные
частные случаи уравнения (5).
Пусть в (5)
![]() ,
тогда уравнение примет вид
,
тогда уравнение примет вид
![]() ,
плоскость в этом случае проходит через
точку
,
плоскость в этом случае проходит через
точку
![]() ,
так как координаты точки О
удовлетворяют этому уравнению.
,
так как координаты точки О
удовлетворяют этому уравнению.
Пусть
![]() ,
тогда получим уравнение
,
тогда получим уравнение
![]() .
В этом случае плоскость параллельна
оси Oz,
так как её нормальный вектор
.
В этом случае плоскость параллельна
оси Oz,
так как её нормальный вектор
![]() перпендикулярен к оси Oz.
В самом деле, здесь проекция вектора
перпендикулярен к оси Oz.
В самом деле, здесь проекция вектора
![]() на ось Oz
равна
на ось Oz
равна
![]() .
Следовательно,
.
Следовательно,
![]() ,
значит, угол
,
значит, угол
![]() .
.
Пусть![]() ,
,
![]() .
Тогда имеем уравнение
.
Тогда имеем уравнение
![]() .
Плоскость проходит через ось Oz,
так как проходит через начало координат
О
(поскольку
.
Плоскость проходит через ось Oz,
так как проходит через начало координат
О
(поскольку
![]() ),
кроме того, она параллельна оси Oz
(поскольку
),
кроме того, она параллельна оси Oz
(поскольку
![]() ).
).
Пусть
![]() ,
,
![]() .
Тогда
.
Тогда
![]() или
или
![]() .
Плоскость параллельна плоскости
.
Плоскость параллельна плоскости
![]() ,
так как она
параллельна оси Oz
(поскольку
,
так как она
параллельна оси Oz
(поскольку
![]() )
и параллельна оси Oy
(поскольку
)
и параллельна оси Oy
(поскольку
![]() ).
).
Пусть
![]() ,
,
![]() ,
,
![]() .
Тогда
.
Тогда
![]() или
или
![]() .
Это уравнение определяет плоскость
.
Это уравнение определяет плоскость
![]() ,
так как плоскость параллельна
,
так как плоскость параллельна
![]() ,
как и в
предыдущем случае, кроме того, она
проходит через точку О
(поскольку
,
как и в
предыдущем случае, кроме того, она
проходит через точку О
(поскольку
![]() ).
Остальные случаи рассматриваются по
аналогии.
).
Остальные случаи рассматриваются по
аналогии.
§3. Угол между двумя плоскостями, условия параллельности и перпендикулярности плоскостей
Пусть в пространстве Oxyz заданы две плоскости соответственно уравнениями
![]() ,
(7)
,
(7)
![]() ,
(8)
,
(8)
где коэффициенты
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() – заданные числа. Тогда векторы
– заданные числа. Тогда векторы
![]() и
и
![]() – нормальные векторы этих плоскостей
(см. рис. 17). За угол
– нормальные векторы этих плоскостей
(см. рис. 17). За угол
![]() между плоскостями (7) и (8) примем один
из двухгранных углов (образованных
ими), равный углу между их нормальными
векторами. Использовав формулу (18) главы
1, определим
между плоскостями (7) и (8) примем один
из двухгранных углов (образованных
ими), равный углу между их нормальными
векторами. Использовав формулу (18) главы
1, определим
![]() . (9)
. (9)
Вычислив по формуле
(9)
![]() ,
найдём угол
,
найдём угол
![]() .
.
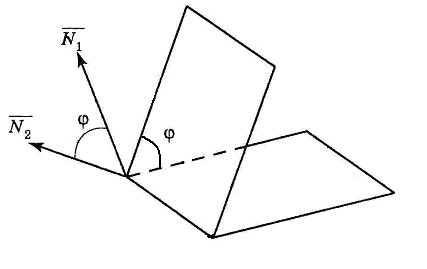 Если
Если
![]() ,
то плоскости (7), (8) параллель-ны между
собой, так как коллинеарны их нормальные
векторы.
,
то плоскости (7), (8) параллель-ны между
собой, так как коллинеарны их нормальные
векторы.
Рис. 17![]() ,
то плоскости (7), (8) перпенди-кулярны
между собой, так как перпендикулярны
их нормаль-ные векторы.
,
то плоскости (7), (8) перпенди-кулярны
между собой, так как перпендикулярны
их нормаль-ные векторы.
