§4. Проекция вектора на ось

П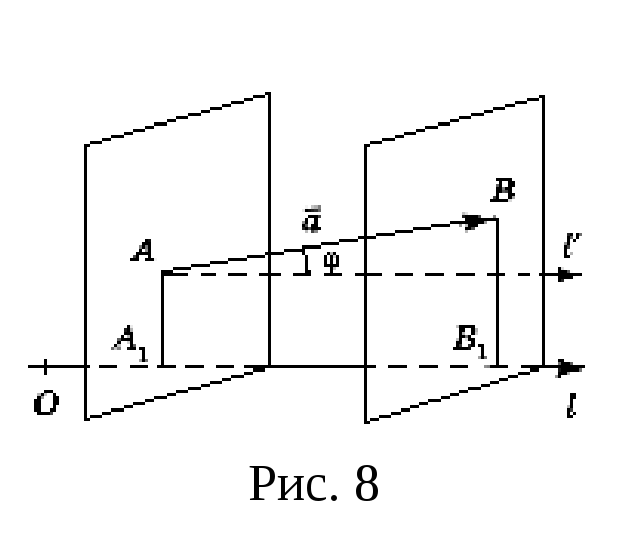усть в пространстве задана некоторая числовая (координатная) ось l с началом в точке = есть вектор, произвольно расположенный в пространстве (рис. 8). Пусть и – проекции на ось l соответственно начала и конца рассматриваемого вектора (т. е. и – точки пересечения с осью пло-скостей, перпендикулярных к оси и проведенных через точки и ); и – соответственно координаты точек и на координатной оси Раз-ность между координатами проекций конца и начала вектора = на ось называется проекцией этого вектора на ось и обозначается пр_l = пр_l. Итак,

. (2)

Под углом между вектором = и осью в пространстве понимается угол между этим вектором и осью . Ось параллельна оси , направлена, как , и проходит через точку – начало вектора. Этот угол всегда считается положительным и измеряется в пределах Легко проверить, что

пр_l=||. (3)

Итак, проекция вектора на ось равна произведению его длины на косинус угла между вектором и осью. Эта формула становится очевидной, если вектор перенести параллельно самому себе так, чтобы его начало лежало на оси например, совпало с точкой .

§5. Разложение вектора по базисным векторам

В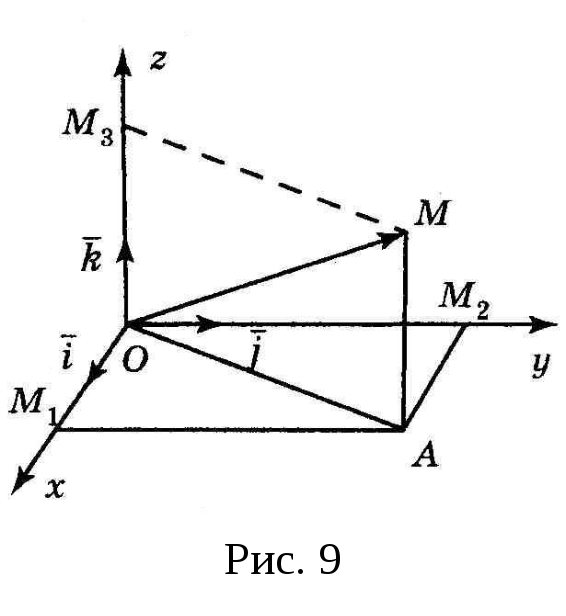озьмем в пространстве прямоугольную декартову систему координат Oxyz. Здесь и в дальнейшем будем считать, что эта система правая, т. е.  такая, для которой поворот от оси к оси на угол, меньший , совершается в направлении против хода часовой стрелки, если смотреть на плоскость из какой-либо точки положительной полуоси Пусть , , – единичные векторы, лежащие на осях и направленные в положительную сторону этих осей, а их начала совпадают с началом координат O (рис. 9), || = || = || = 1. Эти векторы называются базисными (основными).

Пусть – произвольный вектор в системе координат Перенесём его параллельно самому себе так, чтобы начало вектора совпало с точкой О. Получим вектор =. Пусть , и – проекции точки на оси и . Из рис. 9 видно, что

==++, =, =

==++ (4)

Пусть , , – проекции вектора = на оси и . Так как – проекция на ось , то по формуле (2) имеем так как , то

(5)

Пусть =, как показано на рис. 9. В этом случае =||. По формуле (1) имеем =||, но =|| и =, поэтому =. Легко проверить, что эта формула остаётся справедливой при = (при этом вектор будет направлен противоположно ). Аналогично будем иметь =, =. Подставим эти выражения в (4):

=++. (6)

Получили формулу, которая называется разложением вектора по базисным векторам. Коротко ее записывают в виде =(,,), подчёркивая, что задание вектора в пространстве равносильно заданию трёх чисел – проекций этого вектора на оси координат. Числа , , называют также координатами по отношению к базисным векторам , , . Слагаемые векторы правой части (6) называют составляющими вектора

Вектор с началом в точке О – начале координат – называется радиус-вектором точки конца этого вектора. Покажем, что проекции на оси координат радиус-вектора точки равны координатам этой точки.

Пусть точка имеет координаты в рассматриваемой системе По определению абсциссы точки имеем , где – координата точки Но согласно (5) – проекции на ось т. е. Аналогично Итак,