
- •§1. Действительные числа, числовая ось, определители …
- •Глава 1. Элементы векторной алгебры
- •§1. Действительные числа, числовая ось, определители второго и третьего порядков
- •§2. Декартовы координаты. Полярные координаты
- •§3. Векторы, линейные операции над ними
- •§4. Проекция вектора на ось
- •§5. Разложение вектора по базисным векторам
- •§6. Линейные операции над векторами, заданными своими проекциями
- •§7. Длина вектора. Расстояние между двумя точками
- •§8. Направляющие косинусы вектора
- •§9. Скалярное произведение векторов, угол между
- •§10. Векторное произведение векторов, условие коллинеарности двух векторов, площадь треугольника
- •§11. Смешанное произведение векторов и его геометрический смысл. Условие компланарности трех векторов
- •Глава 2. Элементы аналитической геометрии
- •§1. Уравнение поверхности и уравнения линии в пространстве
- •§2. Плоскость, общее уравнение плоскости
- •§3. Угол между двумя плоскостями, условия параллельности и перпендикулярности плоскостей
- •§4. Расстояние от точки до плоскости в пространстве
- •§5. Прямая в пространстве и ее уравнения
- •§6. Канонические уравнения прямой. Уравнения прямой, проходящей через две заданные точки
- •§7. Угол между двумя прямыми, условия параллельности и перпендикулярности
- •§8. Уравнение линии на плоскости
- •§9. Общее уравнение прямой на плоскости, угол между прямыми
- •§10. Уравнение прямой с угловым коэффициентом,
- •§11. Уравнение прямой, проходящей через заданную точку с заданным угловым коэффициентом. Уравнение прямой, проходящей через две заданные точки
- •§12. Кривые второго порядка. Окружность
- •§13. Эллипс
- •§14. Гипербола
- •§15. Парабола
- •§16. Преобразование координат на плоскости
- •§17. Понятие о многомерном евклидовом пространстве
- •§18. Поверхности второго порядка. Сфера. Цилиндр
- •§19. Эллипсоид
- •§21. Однополостный и двуполостный гиперболоиды
- •§22. Эллиптический и гиперболический параболоиды
- •Глава 3. Элементы линейной алгебры
- •§1. Определители высших порядков
- •§2. Свойства определителей
- •§3. Матрицы и действия над ними. Обратная матрица
- •§4. Системы линейных алгебраических уравнений с неизвестными. Матричный метод решения
- •§5. Формулы Крамера
- •§6. Общая система линейных алгебраических уравнений. Метод Гаусса
- •§7. Ранг матрицы. Теорема Кронекера – Капелли
- •§8. Однородные системы
§3. Матрицы и действия над ними. Обратная матрица
Матрицей
называется прямоугольная таблица,
содержащая
![]() чисел,
имеющая
чисел,
имеющая
![]() строк и
строк и
![]() столбцов. Она обозначается
столбцов. Она обозначается
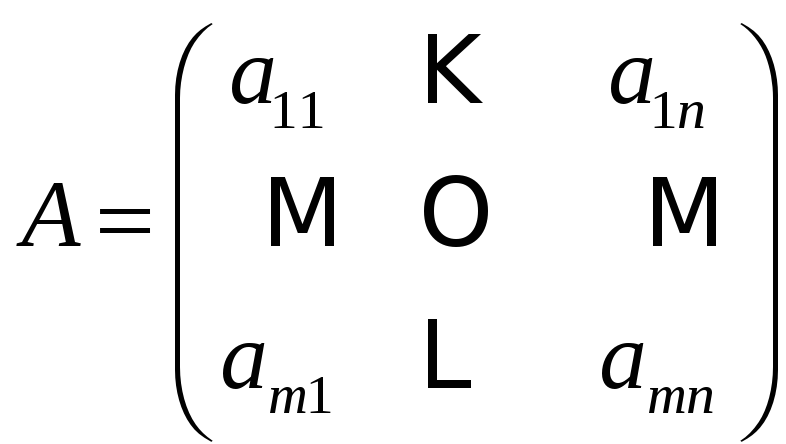 .
.
Числа
![]() называются элементами
матрицы.
Коротко эту матрицу обозначают так:
называются элементами
матрицы.
Коротко эту матрицу обозначают так:
![]() .
Здесь
.
Здесь
![]() – номер строки,
– номер строки,
![]() – номер столбца элемента
– номер столбца элемента
![]() .
Матрицу иногда обозначают и так:
.
Матрицу иногда обозначают и так:
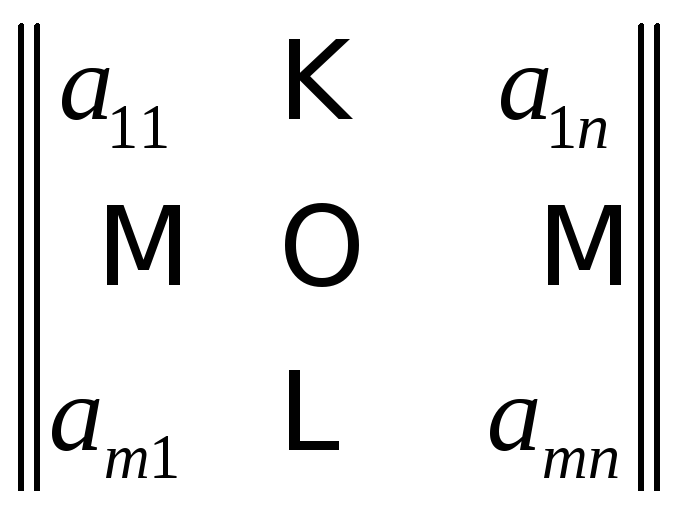 .
.
Если столбцы матрицы сделать строками с теми же номерами, то полученная матрица называется транспонированной и обозначается
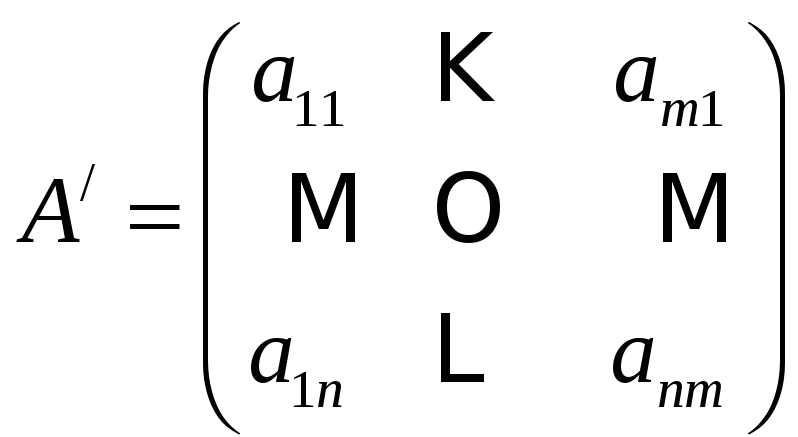 .
.
Если в матрице число строк и число столбцов совпадают, то матрица называется квадратной:
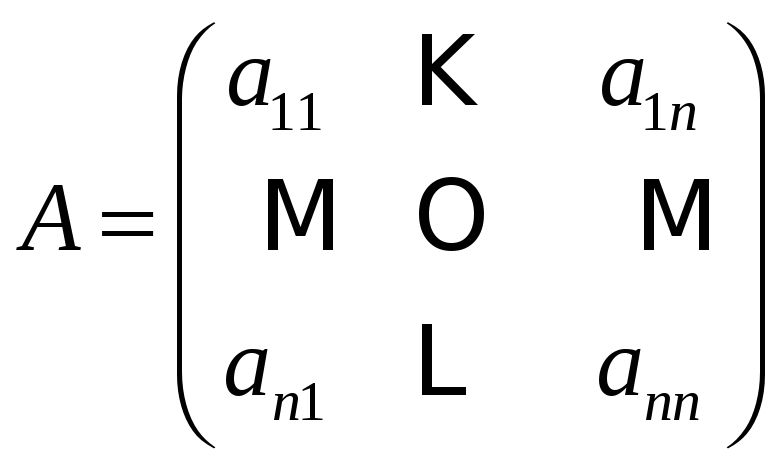 .
.
Элементы
![]() образуют главную
диагональ матрицы.
Число
образуют главную
диагональ матрицы.
Число
![]() называется порядком
матрицы.
Квадратной матрице можно поставить в
соответствие число, называемое
определителем
матрицы,
обозначаемое
называется порядком
матрицы.
Квадратной матрице можно поставить в
соответствие число, называемое
определителем
матрицы,
обозначаемое
![]() и равное
и равное
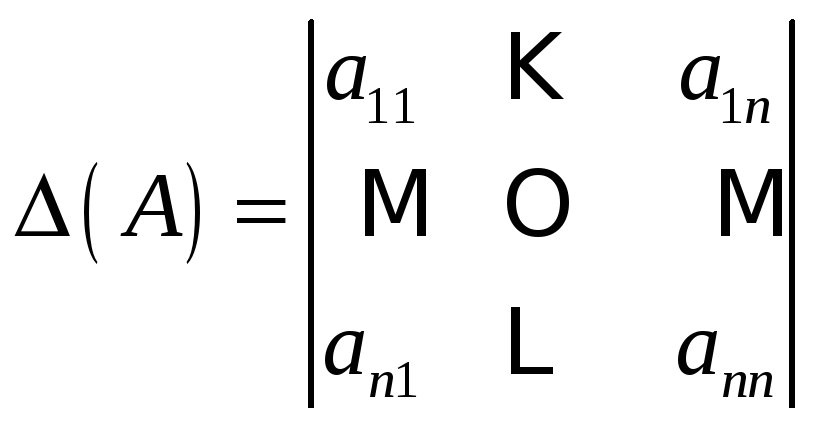 .
.
Матрица, у которой все элементы главной диагонали равны 1, а все остальные элементы равны 0, называется единичной и обозначается
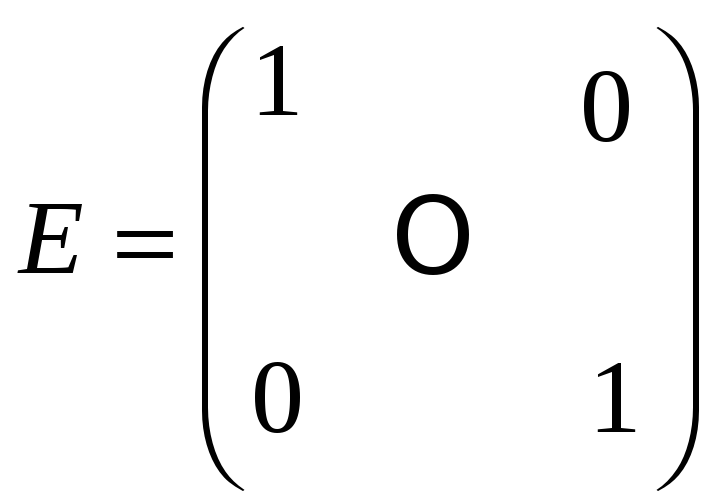 .
.
Матрица, состоящая
из одной строки, называется строчной
и обозначается
![]() .
Матрица, состоящая из одного столбца,
называется столбцевой,
например,
.
Матрица, состоящая из одного столбца,
называется столбцевой,
например,
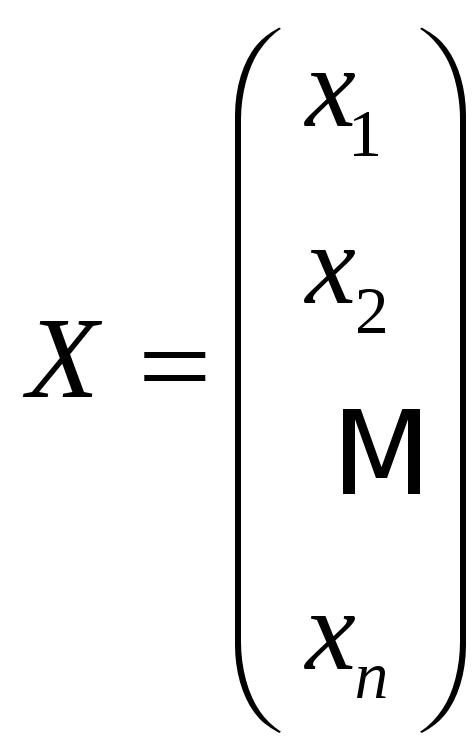 .
.
Пусть
даны две матрицы с одинаковым числом
строк и столбцов:
![]()
![]() Эти матрицы называются равными
друг другу
(при этом пишут
Эти матрицы называются равными
друг другу
(при этом пишут
![]() или
или
![]() ),
если все их соответствующие элементы
равны друг другу, т. е.
),
если все их соответствующие элементы
равны друг другу, т. е.
![]() для всех
для всех
![]()
Суммой
матриц
![]() и
и
![]() называется матрица, обозначаемая
называется матрица, обозначаемая
![]() ,
элементы которой
,
элементы которой
![]() для всех значений
для всех значений
![]() .
Это правило можно записать так:
.
Это правило можно записать так:
![]() .
Аналогично вводится понятие разности
двух матриц.
.
Аналогично вводится понятие разности
двух матриц.
Произведением
матрицы
![]() на число
называется матрица, обозначаемая
на число
называется матрица, обозначаемая
![]() ,
элементы которой равны произведениям
числа
на соответствующие элементы матрицы
,
элементы которой равны произведениям
числа
на соответствующие элементы матрицы
![]() ,
т. е.
,
т. е.
![]() .
Иначе говоря, чтобы умножить матрицу
на число ,
нужно умножить на это число каждый её
элемент (для сравнения заметим, что для
умножения определителя на число нужно
умножить на это число все элементы
какого-либо ряда).
.
Иначе говоря, чтобы умножить матрицу
на число ,
нужно умножить на это число каждый её
элемент (для сравнения заметим, что для
умножения определителя на число нужно
умножить на это число все элементы
какого-либо ряда).
Умножение матриц.
Даны матрица
![]() ,
имеющая
,
имеющая
![]() строк и
строк и
![]() столбцов, и матрица
столбцов, и матрица
![]() ,
имеющая
,
имеющая
![]() строк и
строк и
![]() столбцов. Произведением
этих матриц называется матрица,
обозначаемая
столбцов. Произведением
этих матриц называется матрица,
обозначаемая
![]() (
(![]() – первая матрица), элементы
– первая матрица), элементы
![]() которой определяются формулой
которой определяются формулой
![]() ,
,
![]() ,
,
![]() .
(6)
.
(6)
Изобразим схематично эти матрицы и их произведение:
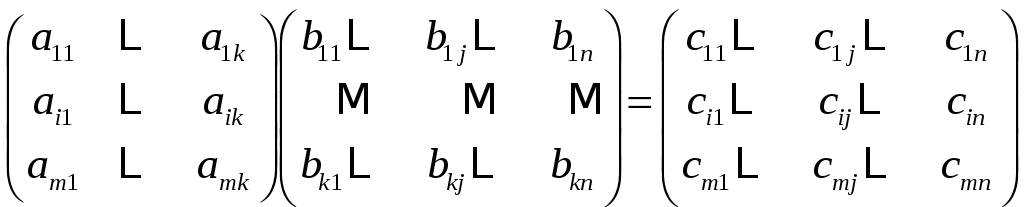 .
.
В формуле (6) первые
индексы означают номера строки элемента
матрицы, вторые – номера столбца
элемента. Формула (6) показывает, что
элемент
![]()
![]() -й
строки и
-й
строки и
![]() -го
столбца матрицы
-го
столбца матрицы
![]() равен сумме произведений элементов
равен сумме произведений элементов
![]() -й
строки первой матрицы
-й
строки первой матрицы
![]() на соответствующие элементы
на соответствующие элементы
![]() -го
столбца второй матрицы
-го
столбца второй матрицы
![]() .
Следовательно, чтобы получить элементы
.
Следовательно, чтобы получить элементы
![]()
![]() -й
строки матрицы
-й
строки матрицы
![]() ,
нужно элементы
,
нужно элементы
![]() -й
строки
-й
строки
![]() умножить на соответствующие элементы
первого столбца
умножить на соответствующие элементы
первого столбца
![]() ,
и, сложив, найти
,
и, сложив, найти
![]() .
Умножив элементы
.
Умножив элементы
![]() -й
строки
-й
строки
![]() на соответствующие элементы второго
столбца
на соответствующие элементы второго
столбца
![]() и сложив, получим
и сложив, получим
![]() и т. д. Умножив элементы
и т. д. Умножив элементы
![]() -й
строки
-й
строки
![]() на соответствующие элементы
на соответствующие элементы
![]() -го
столбца
-го
столбца
![]() и сложив, получим
и сложив, получим
![]() .
.
Таким образом,
элементы
![]() -й
строки матрицы С
получаются с помощью
-й
строки матрицы С
получаются с помощью
![]() -й
строки первой матрицы
-й
строки первой матрицы
![]() .
Это относится к любой строке матрицы
С.
Поэтому ясно, что число строк С
равно числу строк
.
Это относится к любой строке матрицы
С.
Поэтому ясно, что число строк С
равно числу строк
![]() ,
а число столбцов
,
а число столбцов
![]() равно числу столбцов матрицы В,
так как номер столбца
равно числу столбцов матрицы В,
так как номер столбца
![]() элемента
элемента
![]() совпадает с номером столбца
совпадает с номером столбца
![]() матрицы
матрицы
![]() .
.
Аналогично найдём
![]() ,
если число столбцов матрицы
,
если число столбцов матрицы
![]() равно числу строк матрицы
равно числу строк матрицы
![]() .
Если это не так, то произведения
.
Если это не так, то произведения
![]() не существует. Если даже
не существует. Если даже
![]() и
и
![]() существуют, то легко проверить на
примерах, что, вообще говоря,
существуют, то легко проверить на
примерах, что, вообще говоря,
![]() .
.
Свойства умножения
матриц. Пусть
даны три матрицы
![]() ,
,
![]() и
и
![]() .
Тогда:
.
Тогда:
-
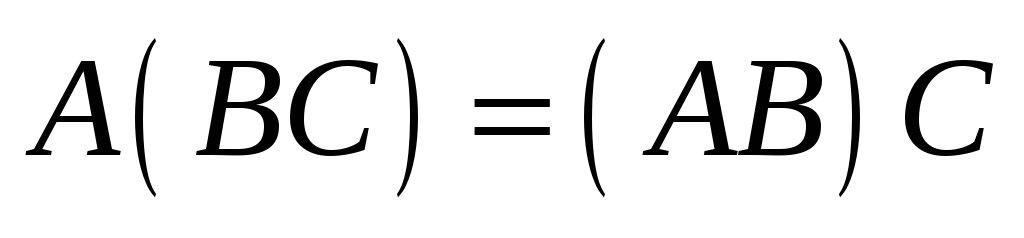 ;
; -
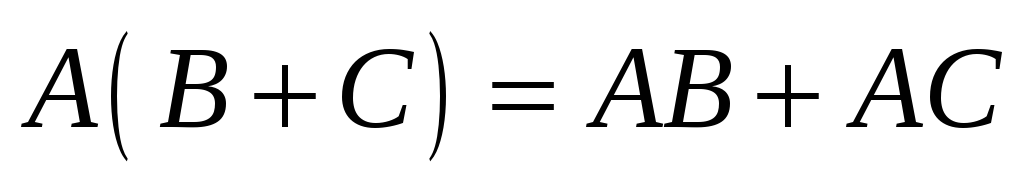 .
.
Пусть
![]() – квадратная матрица, а
– квадратная матрица, а
![]() – единичная матрица того же порядка,
что и
– единичная матрица того же порядка,
что и
![]() .
Нетрудно проверить, что
.
Нетрудно проверить, что
![]() .
.
Обратная матрица. Пусть дана квадратная матрица
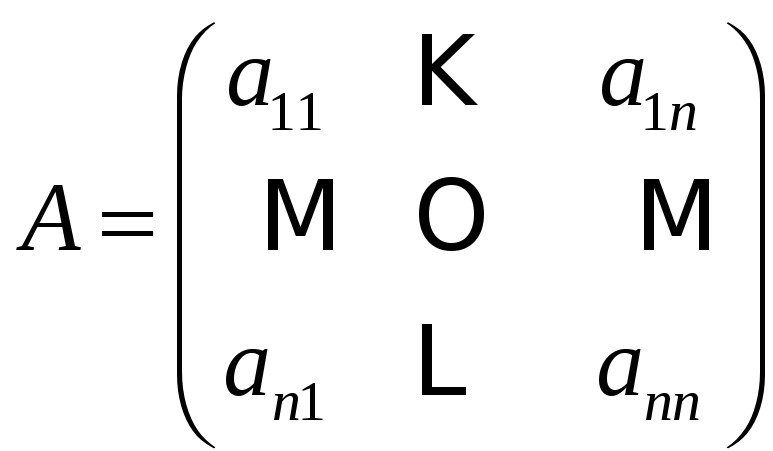
Определитель этой матрицы есть число
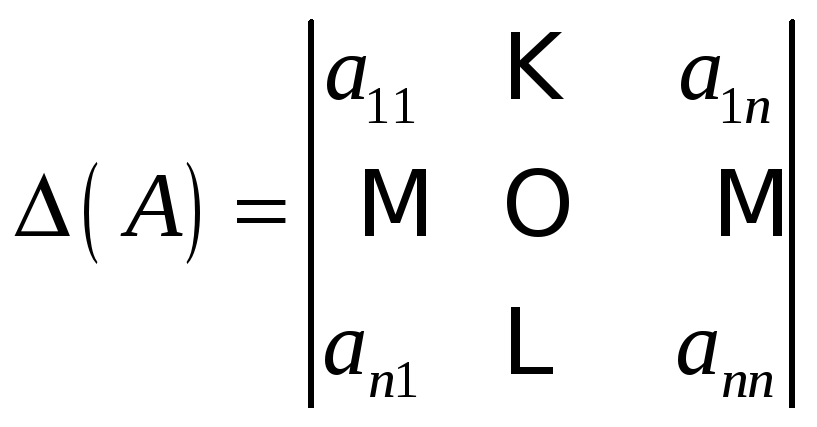 .
.
Пусть этот
определитель не равен нулю и
![]() – алгебраическое дополнение для
элемента
– алгебраическое дополнение для
элемента
![]() .
.
Обратной к данной
матрице
![]() называется матрица, обозначаемая
называется матрица, обозначаемая
![]() и определяемая условиями
и определяемая условиями
![]() Если
Если
![]() то
то
![]() есть матрица вида
есть матрица вида
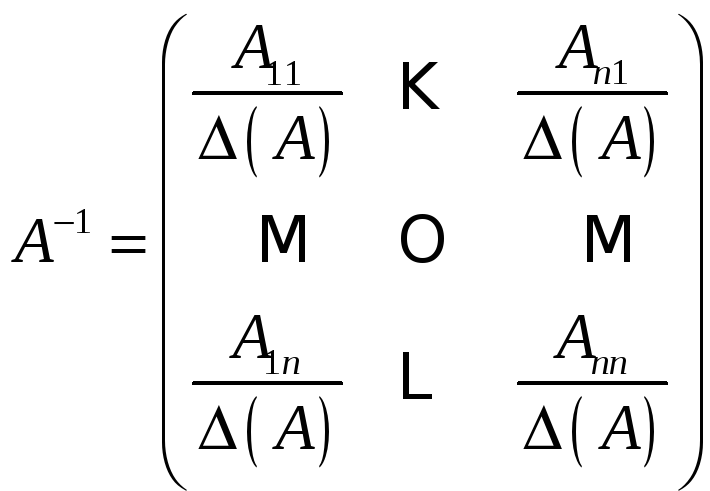 .
.
Отсюда видно, что
для построения обратной матрицы
![]() для матрицы
для матрицы
![]() нужно:
нужно:
-
элементы матрицы
 заменить на их алгебраические дополнения;
заменить на их алгебраические дополнения; -
все эти дополнения поделить на
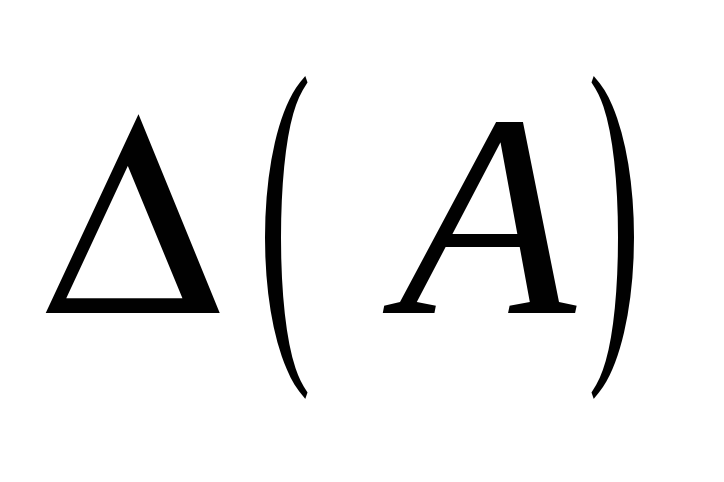 – определитель матрицы
– определитель матрицы
 ;
; -
полученную матрицу транспонировать.
Из приведенного
определения видно, что для нахождения
![]() нужно вычислить определитель матрицы
нужно вычислить определитель матрицы
![]() и все алгебраические дополнения для
всех ее элементов.
и все алгебраические дополнения для
всех ее элементов.
