5.1.3. Упрощенная схема замещения и векторная диаграмма

В силовых трансформаторах, работающих в режимах близких к номинальной нагрузке, обычно пренебрегают током холостого хода . В этом случае Ошибка при этом будет меньше I_0, так как токи суммируются геометрически. При этих допущениях схема замещения изображена на рис. 5.5.

В соответствии с этой упрощенной схемой замещения можно постро-ить упрощенную вектор-ную диаграмму. При ус-ловии, что нагрузка ак-тивно-индуктивная, упро-щенная векторная диа-грамма построена на рис. 5.6.

Вначале откладываем вектор тока , затем вектор напряжения и падения напряжения и , учитывая, что ; . Треугольник АВС представляет собой треугольник короткого замыкания. Если напряжение является заданным, а также известна величина тока нагрузки и ее характер (угол ), то напряжение можно найти путем пристройки к вектору треугольника АВС так, чтобы вершина С лежала на луче, проведенного под углом к оси ординат.

5.1.4. Изменение напряжения на зажимах вторичной обмотки трансформатора при нагрузке

Упрощенная схема замещения и векторная диаграмма значительно облегчает анализ различных режимов работы трансформатора. Известно, что при изменении тока нагрузки напряжение изменяется (см. рис. 5.3). Отклонение от напряжения при холостом ходе и при характеризуется процентным изменением напряжения

(5.4)

Простое выражение для можно получить используя упрощенную схему замещения и векторную диаграмму. Из схемы замещения следует, что . При получим:

. (5.5)

На векторной диаграмме практически . В этом случае . Тогда .

Умножив правую часть на 1, равную , получим

, (5.6)

где называется коэффициентом нагрузки;

активная и реактивная составляющие напряжения короткого замыкания трансформатора (4.33).

При номинальной и активно-индуктивной нагрузке силовых трансформаторов .

З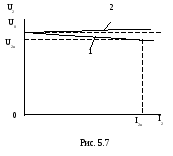ависимость при , называется внешней характеристикой. Её вид при _(инд) изображён на рис. 5.7 (кривая 1).

При изменении нагрузки от холостого хода до напряжение на зажимах вторичной обмотки изменяется на .

При активно-ёмкостной нагрузке отрицателен, второй член в уравнении (5.6) становится отрицательным, и если он будет больше первого члена уравнения, то и будет отрицательной величиной. В этих условиях при увеличении напряжение на зажимах вторичной обмотки будет расти и внешняя характеристика примет вид кривой 2.

5.1.5. Коэффициент полезного действия трансформатора

Преобразование электрической энергии в трансформаторе сопровождается потерями. Потери активной мощности в трансформаторе подразделяются на электрические потери в обмотках и потери в стали.

Электрические потери в обмотках трансформатора равны: и ,

, (5.7)

где потери короткого замыкания трансформатора при номинальном токе.

Потери в стали это потери в сердечнике трансформатора, вызванные вихревыми токами и перемагничиванием. Они зависят от и . При и потери в стали можно считать постоянными, равными потерям холостого хода

. (5.8)

Коэффициент полезного действия определяется по формуле

(5.9)

Мощность, отдаваемая трансформатором, равна

, (5.10)

где коэффициент нагрузки трансформатора;

номинальная мощность трансформатора, кВА.

Сумма потерь

. (5.11)

Тогда выражение для КПД можно записать

. (5.12)

При заданном КПД зависит только от коэффициента нагрузки . Для того чтобы определить, когда КПД достигнет максимального значения необходимо производную приравнять нулю.

Отсюда найдём, что , тогда или

. (5.13)

Обычно трансформаторы проектируются так, чтобы КПД был максимален, тогда .

При передаче реактивной мощности уменьшается, это приводит к уменьшению КПД, как это следует из (5.12).

Обычно трансформаторы проектируются с высоким КПД. В силовых трансформаторах .