8.3. Вкладені цикли. Спрощення структур керування
В прикладі б1) ми зіткнулись з вкладенням циклів, тобто коли один цикл є складовою чаcтиною іншого ціклу. У термінах блок-схем ця сітуація має вигляд:
Два
вкладені цикли
з
передумовою.
Глибіна
вкладення
дорівнює
одиниці
(кількість
вкладених
циклів)
Теоретично глибіна вкладення не обмежена, але рекомендована максимальна глибина дорівнює двом, тобто три цикли послідовно вкладени один в одний.
(i=1,n)
.
.
(j=1,m)
.
.
(k=1,p)
:
.
.
.
.
Більш складна структура робить програму погано читаємою, затруднює її відлагоджування і викликає виникнення помилок. З цим же пов’язана і рекомендована максимальна розмірність масиву, що дорівнює трьом, так як у цьому випадку потрібні три індекси для доступу до елементу масиву і, відповідно, досить організації трьох вкладених циклів для доступу до кожного з елементів.
Загальні правила роботи з вкладеними циклами наступні:
а) глибина вкладеності не повинна перевищувати двох;
б) кордони тіл циклів не повинні перетинатися, тобто один цикл повинен бути повністю вкладений в інший.
(i=1,n)
.
.
(j=1,m) -
неприпустима конструкція
!!!
.
.
.
.
в) зміна циклу (лічильник циклу) не повинна змінюватись у тілі циклу, тобто не повинно бути ніяких присвоєнь нових значень змінній циклу
(i=1,n)
:
i:=1+1
- неприпустимо
також!!!
:
Слід також уникати великої кількості вкладеності умовних структур. Бажано, щоб така вкладеність не перевищувала трьох:
S1
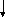
S2
S3
S4
S5
8.4. Робота з двовимірними масивами
Часто при роботі з матрицями суттєвим при розв"язанні задачі виявляється порядок обходу матриці.
-
Обхід по рядках
1 j
n б)1 j
n в) 1 j n г) 1 j n
а
)
1 1 1 1 г) 1
i
i
i
i
m m
m m
При будь-якому обході по рядках необхідно організовувати два вкладених цикли:
зовнішній - по рядках (індекс i)
внутрішній - по стовбцях (індекс j), тобто всередині рядку
Приклад:
а) Вивести елементи матриці у заданому порядку (варіант а)
|Matr
1 n
1
A
є R
m
i,j,n,m
є N
введення n,m,A
(i=1,m)
(j=1,n)
виведення A[i,j]
|end
б) у цьому випадку рух відбувається у зворотньому напрямку (варіант г)
|Matr
1 n
1 A є R
m
i,j,n,m є N
введення n,m,A
-1
(i=m,1)
-1
(j=n,1)
виведення:A[i,j]
|end
2) Обхід по стовпцях
1 j n 1 j n
1 j n 1 j n
а
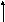
)1
б)1 в)1 г)1
i i i i
m m m m
У випадку обходу по стовбцях:
зовнішній - по стовбцях (індекс j)
внутрішній - по рядках (індекс i).
Приклад: варіант (в):
|Matr
-
n
-
A
є R
m
i,j,n,m є N
введення n,m,A
(j=1,n)
-1
(i=m,1)
виведення A[i,j]
|end
3) Обхід 'змійкою'. Можливі варіанти:
а) б)
в) г)
Д) е)
ж) з)
Приклад: организація обходу по варіанту а)
зовнішній цикл - по рядках (i=1,m)
внутрішній цикл - по стовбцях, припускає два варіанти:
(j=1,n) - для i - непарне.
-1
(j=n,1) - для i - парне.
Вариант 1а. Безпосередне розв’язання задачі:
|Matr1
1 n
1 a є R
AєR
m
i,j,n,m є N
введення n,m,a
(i=1,m)
(i mod 2)<>0 - остача від ділення <>0. Замість цієї
умови
можна 
викристати
флаг логічного
типу, що дорівнює true на непарних
(j=1,n)
рядках і
виведення A[i,j] false на парних (приклад дивись нижче)
-1
(j=n,1)
виведення A[i,j]
|end
Вариант 1б: використання флагу
|Matr1
1 n
1 A є R
m
i,j,n,m є N
введення n,m,A
b:=true
(i=1,m)
(b=true)
(j=1,n)
виведення
A[i,j]
-1
(j=n,1)
виведення A[i,j]
_
b:=b
|end
Варіант 2. Спробуємо спростити структуру керування для організації руху по рядку. Введемо дві додаткові змінні p:=1; q:=n
(j=p,q) (j=1,n)
Тоді рух по рядку зліва направo:
+1
1 n
P q j=p,q
і справа наліво
-1
1 n
Якщо перед кожним наступним проходом виконати переприсвоювання b:=p; p:=q; q:=b; та ввести крок S, з яким змінюється лічильник циклу, то отримаємо наступний алгоритм, у якому порядок проходження рядку змінюється автоматично.
|Matr1
1 n
1 A є R
m
i,j,n,m,p,q,b є N
SєZ
введення n,m,a
p:=1; q:=n; s:=1;
(i=1,m)
s
(j=p,g)
виведення A[i,j]
b:=p; p:=q; q:=b; s:=-s;
|end
Варіант 3. При організації циклу в програмі не завжди зручно змінювати кожен раз напрям кроку (+1/-1 в нашому випадку) При чередуванні кроків можна залишити s=+1, але границі зміни індексу циклу визначити наступним чином:
P q
+1 n
P q
-1 -n
для парних
Однак, індекс елементу масиву може бути тількі цілим додатнім, тому значення змінної циклу слід брати по модулю:
|Matr1
1 n
1 A є R
m
i,n,m, є N
j,p,q,b
є Z
введення n,m,A
p:=1; q:=n;
(i=1,m)
(j=p,g)
виведення A[i,|j|]
b:=-p; p:=-q; q:=b;
|end