
- •1. Сериальные закономерности атомных спектров.
- •19. Влияние межмолекулярных взаимодействий на спектр молекулы.
- •2. Тонкое расщепление атомных спектров. Спин-орбитальное взаимодействие.
- •17. Классификация электронных переходов в молекулах, соотношения между интенсивностями спектральных линий различных типов переходов.
- •3. Систематика спектров многоэлектронных атомов.
- •10. Колебательно-вращательные спектры двухатомных молекул.
- •5. Особенности спектральных термов в приближении “j-j” связи.
- •6. Общая характеристика спектров молекул.
- •7. Вращательные спектры двухатомных молекул в приближении жёсткого ротатора.
- •11. Колебательно-вращательные спектры многоатомных молекул.
- •12. Связь между характером колебаний и интенсивностью колебательных полос поглощения.
- •13. Классификация нормальных колебаний по форме и симметрии молекул.
- •16. Вероятность электронно-колебательных переходов.
- •8. Вращательные спектры многоатомных молекул.
- •18. Методы описания межмолекулярных взаимодействий.
- •20. Изменения спектров поглощения и люминесценции растворов по сравнению со спектрами газов. Принцип Франка-Кондона для межмолекулярных взаимодействий.
- •4. Особенности спектральных термов в приближении “l-s” связи.
- •9. Колебательные спектры двухатомных молекул
- •14. Спектры комбинационного рассеяния молекул
- •15. Электронные состояния двухатомных молекул.
16. Вероятность электронно-колебательных переходов.
Пусть заданы параметры кривых потенциальной энергии состояния, между которыми осуществляются переходы. Рассмотрим, какие из этих переходов наиболее вероятны.

Принцип Франка-Кондона:
Молекула
состоит из двух связанных подсистем,
движение которых совершается с различными
скоростями. Первая
подсистема – это совокупность электронов
(быстрая подсистема, т.к. электронные
переходы осуществляются за время
 с.), а вторая – совокупность ядер
(медленная подсистема, т.к. колебания
ядер происходят с периодом
с.), а вторая – совокупность ядер
(медленная подсистема, т.к. колебания
ядер происходят с периодом
 с).
(68)
с).
(68)
Изменение
свойств электронной оболочки при
поглощении и излучении кванта происходит
так быстро, что скорости и положения
ядер при этом измениться не успевают.
Следовательно, в процессе
электронно-колебательных переходов
молекула оказывается в возбужденном
электронном состоянии при том же
значении межъядерного расстояния, в
каком она была до поглощения. На диаграмме
кривых потенциальной энергии наиболее
вероятными будут являться переходы,
осуществляемые вдоль вертикальных
линий. Т.к. при колебании молекулы ядра
большую часть времени находятся в
областях, близких к потенциальной
кривой, следовательно, наиболее
вероятными будут переходы, которые
начинаются и заканчиваются именно в
этих областях. Исключение составляет
невозбужденные колебательные состояния,
в которых молекула находится при
значениях
 .
.
Для многоатомной молекулы наиболее вероятными будут являться те переходы, для которых максимален фактор Франка-Кондона. Фактором Франка-Кондона называют

 -i-ое
колебательное стояние 1-го электронного
уровня;
-i-ое
колебательное стояние 1-го электронного
уровня;
 -
j-ое
колебательное состояние 2-го электронного
уровня.
-
j-ое
колебательное состояние 2-го электронного
уровня.
Важным фактором, определяющим характер спектра многоатомных молекул, является взаимодействие различных нормальных колебаний. Проявляется это взаимодействие в том, что после возбуждения какой-либо колебательной степени свободы энергия этого колебания за достаточно короткое время перераспределяется между другими нормальными колебаниями, приводя к сокращению времени жизни возбужденного состояния. Это приводит к уширению электронно-колебательных уровней и спектров. Такое явление особенно характерно для многоатомных молекул низкой симметрии. Исходя из этого, все электронно-колебательные и электронно-колебательно-вращательные переходы сопровождаются излучением в виде широких полос.
В зависимости от степени связи между нормальными колебаниями, а также между электронным и колебательным движениями молекулы, их подразделяют на простые, полусложные и сложные. К простым молекулам относятся симметричные 2-х атомные молекулы, для них характерен квазилинейчатый спектр. Для полусложных – структурный спектр, для сложных – сплошной бесструктурный спектр.
------------------------------------------------------------
8. Вращательные спектры многоатомных молекул.
У
многоатомных молекул в отличие от
двухатомных возможно вращение вокруг
3-х взаимно перпендикулярных осей в
пространстве. Для
молекулы характерны моменты инерции
 ,
,
 ,
,
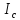 .
Соотношение между этими моментами
инерции определяется симметрией
молекулы.
.
Соотношение между этими моментами
инерции определяется симметрией
молекулы.
В зависимости от соотношения между моментами инерции многоатомных молекул можно отнести к одному из 3-ех типов ротатора:
1)
 - сферический ротатор;
- сферический ротатор;
2)
 - симметричный ротатор;
- симметричный ротатор;
3)
 - асимметричный ротатор. (45)
- асимметричный ротатор. (45)
Энергия вращательного движения для сферического ротатора имеет такой же вид, как нежесткого ротатора 2-х атомной молекулы. Для симметричного ротатора энергия вращательного движения многоатомной молекулы:

В этом выражении:
k – первое вращательное квантовое число; k = 0,1…
j – второе квантовое число; j = k, k+1, k+2.
Даже для молекул достаточно высокой симметрии система вращательных уровней намного сложнее, чем система вращательных уровней 2-х атомных молекул. Из многоатомных соединений чисто вращательным спектром обладают не только полярные молекулы, в которых атомы связаны ионной или ковалентной полярной связью, но и молекулы у которых дипольный момент и, следовательно, вращательный моменты импульса появляются при колебаниях. У некоторых молекул вращательные спектры не регистрируются в разряженных газах, но его можно зарегистрировать в жидкостях.
