
- •1. Броуновское движение
- •2. Законы идеального газа
- •3. Барометрическая формула.
- •4. Основное уравнение молекулярно-кинетической
- •5. Распределение Максвелла
- •6. Средняя длина свободного пробега
- •Vмол30 1030 м3, м.
- •7. Явления переноса
- •Диффузия в газах
- •8. Внутреннее трение
- •Теплопроводность
- •9. Первое начало термодинамики
- •10. Классическая теория теплоемкости
- •11. Адиабатический процесс
- •12. Политропический процесс
- •13. Энтропия. Второе и третье начала термодинамики
- •14. Расчет изменения энтропии в процессах
- •15. Цикл Карно. Второе начало термодинамики
- •16. Реальные газы. Критическое состояние
- •17. Уравнение Ван-дер-Ваальса
- •18. Особенности жидкого состояния вещества
- •19. Свободная энергия как функция состояния
- •Поверхностное натяжение
- •20. Условия равновесия на границах различных сред
- •21. Формула Лапласа
- •22. Фаза. Фазовое равновесие. Общая характеристика фазовых переходов 1-го и 2-го рода
- •23. Уравнение Клапейрона Клаузиуса.
- •24. Эффект Джоуля-Томсона
- •25. Методы получения низких температур
- •26. Термодинамическая шкала температур.
- •27. Симметрия кристаллов. Дефекты в кристаллах
- •Классическая теория теплоемкости твердых тел
- •28. Понятие о квантовой статистике. Распределения
- •29. Понятие о квантовой теории теплоемкости.
- •Рекомендуемая литература*
6. Средняя длина свободного пробега
и число столкновениЙ
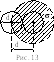
Минимальное расстояние, на которое сближаются центры двух молекул при столкновении, называется эффективным диаметром молекулы d, а величина = d2 эффективным сечением молекулы (рис. 13).
Средняя длина свободного пробега молекулы – это прямолинейный участок пути, проходимый молекулой между двумя последовательными соударениями.
П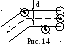 усть
имеется газ с концентрацией n
и движется только одна молекула, а
остальные неподвижны. За 1 с эта молекула
пройдет путь, равный ее средней скорости
υ,
и столкнется со всеми молекулами, центры
которых расположены в ломаном цилиндре
длиной υ
и площадью основания, равной эффективному
сечению (рис. 14). Умножив объем цилиндра
на концентрацию n,
получим число столкновений: '
= d2
υ
n.
усть
имеется газ с концентрацией n
и движется только одна молекула, а
остальные неподвижны. За 1 с эта молекула
пройдет путь, равный ее средней скорости
υ,
и столкнется со всеми молекулами, центры
которых расположены в ломаном цилиндре
длиной υ
и площадью основания, равной эффективному
сечению (рис. 14). Умножив объем цилиндра
на концентрацию n,
получим число столкновений: '
= d2
υ
n.
В
действительности движется не одна, а
все молекулы, поэтому в последнюю формулу
должна входить не средняя скорость
относительно стенок сосуда, а скорость
относительно других молекул. Можно
доказать, что υОТН
![]() υ.
Поэтому, среднее число столкновений за
1 с равно:
υ.
Поэтому, среднее число столкновений за
1 с равно:
![]() .
(24)
.
(24)
Средняя
длина свободного пробега
равна отношению длины пути, пройденного
молекулой, к числу испытанных ею на этом
пути столкновений:
![]() .
(25)
.
(25)
Таким образом, длина свободного пробега молекул тем меньше, чем больше их концентрация и эффективное сечение.
Оценим порядок величин длины свободного пробега и числа соударений (т.е. необходимо найти d и n). Для нахождения d вспомним, что в жидкостях молекулы располагаются достаточно плотно друг к другу. Один моль воды (18 г) занимает объем 18 см3 = 18 10 6 м3. Разделив объем одного моля на число молекул в одном моле NA, получим приблизительно объем одной молекулы и ее линейный размер:
Vмол30 1030 м3, м.
При испарении воды размер молекулы d не изменяется, но теперь один моль любого газа (и водяного пара) при нормальных условиях занимает объем 22,4 103 м3. Разделив число молекул в одном моле NA на объем одного моля газа, получим концентрацию n:
n = 6 1023 / 22,4 10 –3 3 1025 м 3.
Подставим найденные d и n в формулу (25):
=
1 / (![]()
9 10
–20
3 1025)
10 7
м.
9 10
–20
3 1025)
10 7
м.
Пусть средняя скорость молекулы воды (пара) равна 600 м/с. Тогда из формулы (25) можно найти число столкновений:
![]() 6
10
9
c1.
6
10
9
c1.
Естественно возникает вопрос, можно ли считать идеальным газ, в котором молекулы каждую секунду сталкиваются миллиарды раз, т.е. "взаимодействуют". Однако длина свободного пробега в 100–1000 раз больше размеров молекулы. Другими словами, время столкновения молекул примерно в 100–1000 раз меньше времени между столкновениями. Следовательно, подавляющую часть времени молекулы движутся свободно.
Состояние газа в сосуде называется вакуумом, если длина свободного пробега сравнима с линейными размерами сосуда или превышает их. Газ в этом случае называют ультраразряженным. Различные степени вакуума (низкий, средний, высокий, сверхвысокий) создаются в разных технических устройствах (лампы накаливания, радиолампы, электронно-лучевые трубки телевизоров, системы вакуумного напыления металлов и т.п.).
