2. Векторное и смешанное произведение.

Множество всех ортонормированных троек векторов можно разбить на два класса. Будем говорить, что тройка имеет левую ориентацию, если со стороны первого вектора тройки движение (по кратчайшему пути) от второго к третьему по часовой стрелке, в противном случае тройка имеет правую ориентацию.

Векторным произведением векторов a и b называется вектор, удовлетворяющий следующим трём условиям:

1. Длина вектора 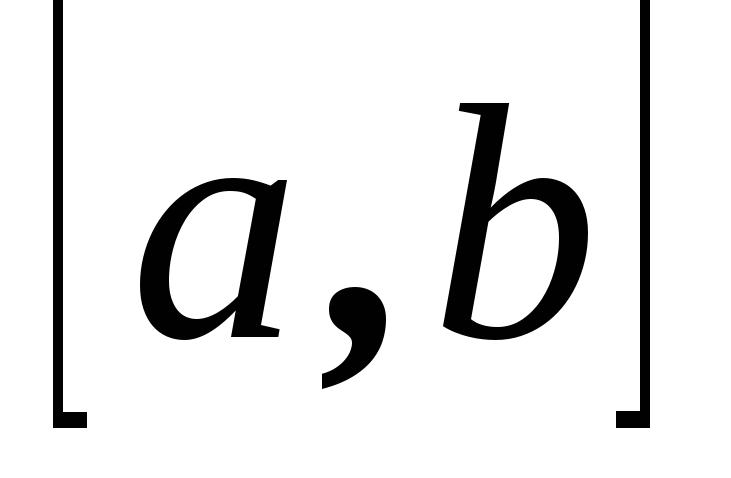равна площади параллелограмма натянутого на векторы a,b.

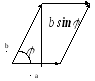2. Вектор 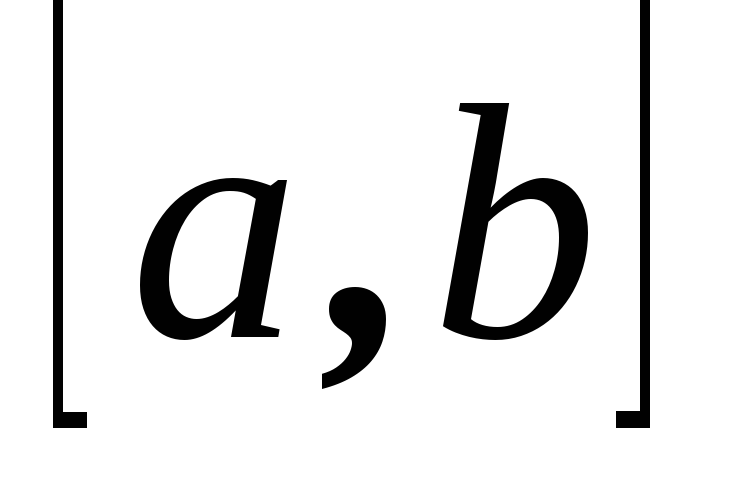ортогонален векторам a и b.

3. Тройка векторов a,b, 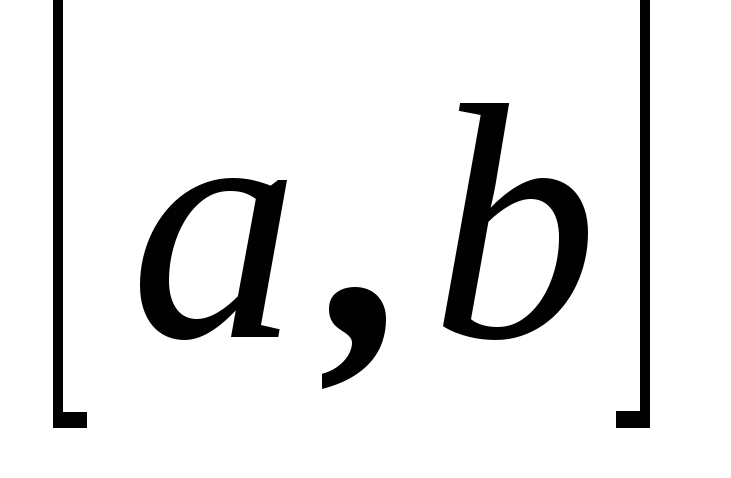– имеет правую ориентацию.

Из определения вытекает, что . Если векторы a,b коллинеарные, то векторное произведение равно 0. Приведём свойства векторного произведения.

Свойство 8.27 Векторное произведение антикоммутативно, то есть .

Действительно, модуль векторного произведения не зависит от порядка сомножителей. Далее, вектор коллинеарен вектору . Однако, переставляя множителей, мы должны изменить направление произведения, чтобы было выполнено условие 3.

Смешанным произведением векторов a,b,c называется число и обозначается .

Свойство 8.28 Смешанное произведение векторов по модулю равно объёму параллелепипеда натянутого на тройку векторов . Знак смешанного произведения определяется ориентацией тройки векторов , плюс – если тройка правая и минус – если левая.

Доказательство. По определению смешанного произведения , где - угол между вектором и векторным произведением , а - угол между векторами и . Произведение равно высоте параллелепипеда, а - площади основания параллелепипеда. Произведение этих величин равно объёму параллелепипеда. Знак произведения определяется знаком . Если угол острый, то тройка векторов правая и смешанное произведение положительно. Если угол тупой, то тройка левая и знак смешанного произведения отрицательный.

Свойство 8.29 .

Для доказательства достаточно заметить, что по модулю все приведённые величины равны и совпадают с объёмом параллелепипеда, натянутого на векторы , а знак определяется в зависимости от ориентации тройки векторов.

Свойство 8.30.

Доказательство. Рассмотрим смешанное произведение . Выпишем цепочку равенств, используя свойства смешанного и скалярного произведения: . Вычтем из левой части равенства правую и получим равенство справедливое при любом выборе x. Положим , тогда и, значит, .

Свойство 8.31

Доказательство. .

Выразим координаты векторного произведения через координаты исходных векторов в правом ортонормированном базисе. Пусть и . Используя свойства векторного произведения, найдём , и . Поскольку базис ортонормированный, то

первая координата равна , вторая координата и третья координата . Таким образом, векторное произведение может быть получено в результате раскрытия по третьему столбцу символического определителя .

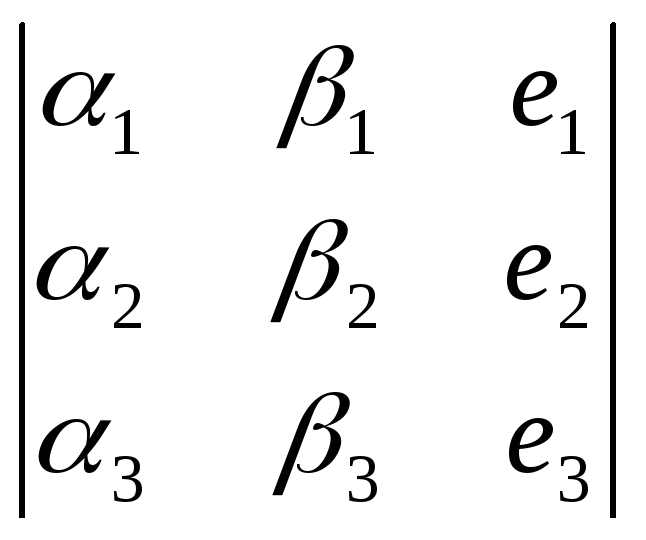Выразим смешанное произведение через координаты исходных векторов в ортонормированном базисе. Разложим векторы a,b,c по базису , , . Раскроем смешенное произведение . Выражение в правой части есть определитель матрицы .

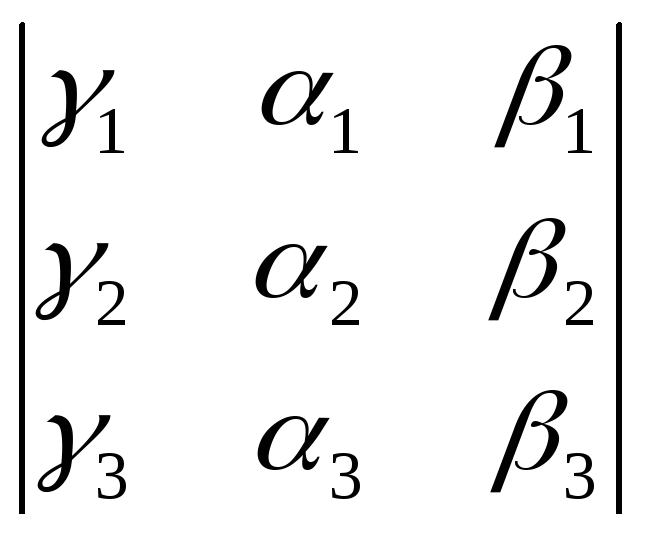Таким образом, определитель матрицы, составленной из координат векторов по абсолютной величине равен объёму параллелепипеда натянутого на эти вектора, а его знак показывает ориентацию этой тройки векторов. Знак положителен, если ориентация совпадает с ориентацией базисных векторов и отрицателен, если ориентации не совпадают.

Матрица Грама от трёх векторов, заданных в ортонормированном базисе равна произведению матриц , следовательно, определитель матрицы Грама равен квадрату объёма параллелепипеда натянутого на эти векторы.