
- •Натуральные числа
- •Метод математической индукции.
- •Бином Ньютона, треугольник Паскаля
- •Целые числа
- •Рациональные числа
- •Числовые кольца, поля
- •Вещественные числа
- •Поле комплексных чисел
- •Комплексная плоскость.
- •Извлечение корней, корни из единицы
- •Делимость многочленов. Наибольший общий делитель. Алгоритм Евклида. Расширенный алгоритм Евклида.
- •Разложение рациональных функций в сумму дробей.
- •Неприводимый многочлен, его свойства
- •Из вытекает, либо , либо .
- •Если неприводимый многочлен делится на неприводимый многочлен, то они отличаются числовым множителем.
- •Корень многочлена.
- •Интерполяционный многочлен
- •Интерполяционный многочлен в форме Лагранжа
- •Интерполяционный многочлен в форме Ньютона
- •Разложение многочлена над полем рациональных чисел
- •Примитивный многочлен, его свойства
- •Критерий Эйзенштейна
- •Все коэффициенты многочлена f(X), кроме старшего, делятся на p
- •Старший коэффициент не делится на p
- •Свободный член не делится на
- •Метод Кронекера разложения многочлена на неприводимые многочлены над кольцом целых чисел.
- •Рациональные корни.
- •Присоединение корня. Поле разложения многочлена.
- •Формальная производная, ее свойства
- •Производные высоких порядков
- •Интерполяционный многочлен Лагранжа-Сильвестра
- •Формулы Виета
- •Симметрические полиномы
- •Формулы Кардано
- •Способ Феррари
- •Дискриминант
- •Основная теорема Алгебры
- •Разложение многочлена на неприводимые множители над полем вещественных чисел
- •Теорема Штурма
- •Любые два соседних многочлена не имеют общих корней
- •Последний многочлен не имеет вещественных корней.
- •Если в окрестностях корня a многочлена сам многочлен возрастает, то , а если убывает, то
- •Метод Гаусса решения системы линейных уравнений
- •Равносильные преобразования
- •Умножение строки не ненулевое число.
- •Перестановка строк
- •Прибавление к некоторой строке другой строки, умноженной на число.
- •Метод Гаусса.
- •Перестановки
- •Четность перестановок
- •Определитель
- •Свойства определителя
- •Изменит знак при перестановке столбцов
- •Равен нулю, если имеется два одинаковых столбца
- •Не изменится при прибавлении к столбцу другого столбца, умноженного на число.
- •Вычисление определителей произвольных порядков
- •Определитель Вандермонда
- •Теорема Лапласа
- •Умножение матриц
- •Формула Бине-Кощи
- •Операции с матрицами
- •Обратная матрица
- •Правило Крамера
- •Матрица элементарных преобразований
- •Построение обратной матрицы
- •Блочные матрицы
- •Алгоритм Штрассена
- •Кронекерово произведение
- •Формула Фробениуса
- •Линейные пространства.
- •. Линейная зависимость. Теорема о замене. Ранг системы.
- •Конечномерные пространства. Базис. Размерность. Дополнение до базиса. Базис суммы, пересечения.
- •. Прямая сумма подпространств. Проекция.
- •Изменение координат вектора при изменении базиса.
- •Изоморфизм линейных пространств.
- •Задание прямой и плоскости в пространстве. Деление отрезка. Задачи.
- •Ранги матрицы.
- •Общее решение системы линейных уравнений.
- •Двойственное пространство
- •Взаимное расположение линейных многообразий в пространстве.
- •Геометрия на плоскости и в пространстве.
- •Скалярное произведение.
- •Симметричность .
- •Векторное и смешанное произведение.
- •Уравнение прямой и плоскости в пространстве
- •Евклидово пространство. Скалярное произведение.
- •Изменение матрицы Грама при изменении базиса.
- •Ортогональность.
-
Изоморфизм линейных пространств.
Определение 7.35 Линейные пространства над числовым полем P называются изоморфными, если существует взаимно однозначное соответствие между векторами этих пространств, сохраняющее операции сложения векторов и умножения на скаляр.
Для доказательства
изоморфизма линейных пространств V
и W
требуется построить взаимно однозначное
отображение
![]() ,
обладающее свойствами сохранения
операции:
,
обладающее свойствами сохранения
операции:
-
 ,
,

-
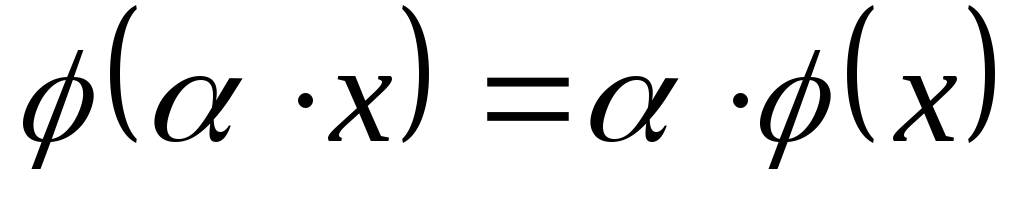 ,
,

Следствие 7.24. При изоморфизме нулевой вектор переходит в нулевой вектор.
Доказательство.
Действительно,
![]() .
.
Лемма 7.14 Пусть V, W, U линейные пространства над полем P. Пусть W изоморфно V, а V изоморфно U, тогда W изоморфно U.
Доказательство.
По условию существуют взаимно однозначные
соответствия
![]() и
и
![]() ,
обладающие свойствами сохранения
операции, то есть
,
обладающие свойствами сохранения
операции, то есть
-
 ,
,

-
 ,
,

-
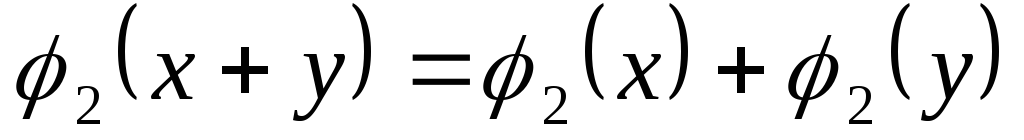 ,
,

-
 ,
,

Отображение
![]() ,
получаемое последовательным применением
,
получаемое последовательным применением
![]() и
и
![]() ,
является взаимно однозначным соответствием
между пространством W
и пространством U.
Далее, имеем
,
является взаимно однозначным соответствием
между пространством W
и пространством U.
Далее, имеем
-
 ,
где
,
где
 .
. -
 ,
,
 .
.
Тем самым изоморфизм установлен.
Лемма 7.15 Пространство
V
над числовым полем P
размерности n
изоморфно арифметическому пространству
![]() .
.
Доказательство.
Пусть
![]() - базис V.
Каждому вектору x
из V
поставим в соответствие его координаты.
Данное соответствие является взаимно
однозначным (Теорема 7 .39) и сохраняет
операции. Тем самым изоморфизм установлен.
- базис V.
Каждому вектору x
из V
поставим в соответствие его координаты.
Данное соответствие является взаимно
однозначным (Теорема 7 .39) и сохраняет
операции. Тем самым изоморфизм установлен.
Лемма 7.16. При изоморфизме базис переходит в базис.
Доказательство.
Пусть
![]() - изоморфизм пространства V
на W,
- изоморфизм пространства V
на W,
![]() - базис V.
Разложим произвольный вектор x
из V
по базису
- базис V.
Разложим произвольный вектор x
из V
по базису
![]() .
По определению изоморфизма
.
По определению изоморфизма
![]() ,
и значит, в силу взаимно однозначности
отображения, через систему векторов
,
и значит, в силу взаимно однозначности
отображения, через систему векторов
![]() линейно выражается любой вектор
пространства W.
Методом от противного покажем линейную
независимость системы векторов
линейно выражается любой вектор
пространства W.
Методом от противного покажем линейную
независимость системы векторов
![]() .
Пусть не так, тогда найдутся числа
.
Пусть не так, тогда найдутся числа
![]() ,
не все равные нулю, что
,
не все равные нулю, что
![]() .
Последнее равенство, используя свойства
изоморфизма, запишем в виде
.
Последнее равенство, используя свойства
изоморфизма, запишем в виде
![]() .
В силу взаимно однозначности изоморфизма
выводим
.
В силу взаимно однозначности изоморфизма
выводим
![]() ,
т.е. система векторов
,
т.е. система векторов
![]() - линейно зависима. К полученному
противоречию с условиями нас привело
допущение о линейной зависимости системы
векторов
- линейно зависима. К полученному
противоречию с условиями нас привело
допущение о линейной зависимости системы
векторов
![]() .
Таким образом, система векторов
.
Таким образом, система векторов
![]() является полной линейно независимой
системой, т.е. базисом линейного
пространства W.
является полной линейно независимой
системой, т.е. базисом линейного
пространства W.
Теорема 7.45. Линейные пространства V и W над полем P изоморфны тогда и только тогда, когда их размерности равны.
Доказательство.
Если размерности пространств V
и W
совпадают и равны n,
то оба пространства изоморфны
![]() (Лемма 7 .15),
а, значит и между собой (Лемма 7 .14).
Обратно, если пространства изоморфны,
то при изоморфизме базис переходит в
базис (Лемма 7 .16), и, значит, размерности
пространств равны.
(Лемма 7 .15),
а, значит и между собой (Лемма 7 .14).
Обратно, если пространства изоморфны,
то при изоморфизме базис переходит в
базис (Лемма 7 .16), и, значит, размерности
пространств равны.
Изоморфизм пространств позволяет переносить терминологию, принятую в одном пространстве на изоморфные пространства. Например, можно говорить о прямой в пространстве многочленов.
-
Задание прямой и плоскости в пространстве. Деление отрезка. Задачи.
Опишем множество точек, лежащих на
прямой l, проходящей через
точки A, B.
Если
![]() ,
то векторы
,
то векторы
![]() и
и
![]() коллинеарные, т.е отличаются числовым
множителем. Пусть
коллинеарные, т.е отличаются числовым
множителем. Пусть
![]() .
Выразим отсюда x:
.
Выразим отсюда x:
![]() .
Данное уравнение называется параметрическим
уравнением прямой. Вектор A-B
принадлежит прямой и называется
направляющим вектором прямой.
.
Данное уравнение называется параметрическим
уравнением прямой. Вектор A-B
принадлежит прямой и называется
направляющим вектором прямой.
В зависимости от параметра
![]() получаем различные точки прямой. Если
получаем различные точки прямой. Если
![]() ,
то получим точку X из
отрезка
,
то получим точку X из
отрезка
![]() ,
причём
,
причём
![]() .
Если
.
Если
![]() ,
то получаем точку X, что
отрезок
,
то получаем точку X, что
отрезок
![]() содержит точку A, причём
содержит точку A, причём
![]() .
Если
.
Если
![]() ,
то получаем точку X, что
отрезок
,
то получаем точку X, что
отрезок
![]() содержит точку B, причём
содержит точку B, причём
![]() .
.
Пусть A,B,C
три точки не лежащие на одной прямой.
Опишем множество точек плоскости
![]() ,
проходящей через эти три точки. Точка
x лежит на плоскости тогда
и только тогда, когда вектор x-A
является линейной комбинацией векторов
B-A и C-A.
Следовательно, параметрическое уравнение
плоскости имеет вид
,
проходящей через эти три точки. Точка
x лежит на плоскости тогда
и только тогда, когда вектор x-A
является линейной комбинацией векторов
B-A и C-A.
Следовательно, параметрическое уравнение
плоскости имеет вид
![]() .
Векторы B-A
и C-A называются
направляющими векторами плоскости.
.
Векторы B-A
и C-A называются
направляющими векторами плоскости.
В

![]()
![]() получаются точки из разных областей.
На рисунке приведено разбиение на
области и указаны значения параметров.
получаются точки из разных областей.
На рисунке приведено разбиение на
области и указаны значения параметров.
Пусть система векторов
![]() - линейно не зависима. Множество точек
вида
- линейно не зависима. Множество точек
вида
![]() называется линейным многообразием.
называется линейным многообразием.
Для иллюстрации приведённой теории решим следующую задачу:
Доказать, что в произвольном тетраэдре, все отрезки соединяющие вершины с точкой пересечения медиан треугольника, образованного вершинами противоположной грани, пересекаются в одной точке и найти отношение, в котором делит эти отрезки точка пересечения.
В начале решим вспомогательную задачу:
выразить точку пересечения медиан
треугольника через его вершины. Обозначим
вершины треугольника через A,B,C.
Векторы AB и AC
выберем в качестве базиса. Тогда, точки
имеют координаты A=(0,0),
B=(1,0), C=(0,1).
Обозначим середину отрезка [BC]
через F. Точка F
имеет координаты (1/2,1/2). Отрезок [AF]
делится точкой пересечения медиан O
в соотношении 2:1, следовательно,
O=(1/3,1/3). Таким образом,
![]() .
Рассматривая плоскость как линейное
многообразие, получаем
.
Рассматривая плоскость как линейное
многообразие, получаем
![]() .
Обозначим через ABCD вершины
тетраэдра. В качестве базиса выберем
векторы AB, AC,
AD. Тогда A=(0,0,0),
B=(1,0,0), C=(0,1,0),
D=(0,0,1). Точку пересечения
медиан треугольника BCD
обозначим через F,
треугольника ACD – через
G. Координаты этих точек
равны F=(1/3,1/3,1/3), G=(0,1/3,1/3).
Параметрическое уравнение прямой AF
имеет вид x=a(1/3,1/3,1/3),
а прямой BG x=(1,0,0)+b(-1,1/3,1/3).
Точка пересечения H этих
прямых находится из системы уравнений
a(1/3,1/3,1/3)=(1,0,0)+b(-1,1/3,1/3)
и H=(1/4,1/4,1/4) (получается
при a=b=3/4).
Отрезки AF и BG
в точке пересечения делятся в отношении
3:1. Выбирая в качестве B
любую вершину тетраэдра (отличную от
A) получим, что все отрезки
соединяющие вершины с точкой пересечения
медиан треугольника, образованного
вершинами противоположной грани,
пересекаются в одной точке H
и делятся в отношении 3:1.
.
Обозначим через ABCD вершины
тетраэдра. В качестве базиса выберем
векторы AB, AC,
AD. Тогда A=(0,0,0),
B=(1,0,0), C=(0,1,0),
D=(0,0,1). Точку пересечения
медиан треугольника BCD
обозначим через F,
треугольника ACD – через
G. Координаты этих точек
равны F=(1/3,1/3,1/3), G=(0,1/3,1/3).
Параметрическое уравнение прямой AF
имеет вид x=a(1/3,1/3,1/3),
а прямой BG x=(1,0,0)+b(-1,1/3,1/3).
Точка пересечения H этих
прямых находится из системы уравнений
a(1/3,1/3,1/3)=(1,0,0)+b(-1,1/3,1/3)
и H=(1/4,1/4,1/4) (получается
при a=b=3/4).
Отрезки AF и BG
в точке пересечения делятся в отношении
3:1. Выбирая в качестве B
любую вершину тетраэдра (отличную от
A) получим, что все отрезки
соединяющие вершины с точкой пересечения
медиан треугольника, образованного
вершинами противоположной грани,
пересекаются в одной точке H
и делятся в отношении 3:1.
