
- •Натуральные числа
- •Метод математической индукции.
- •Бином Ньютона, треугольник Паскаля
- •Целые числа
- •Рациональные числа
- •Числовые кольца, поля
- •Вещественные числа
- •Поле комплексных чисел
- •Комплексная плоскость.
- •Извлечение корней, корни из единицы
- •Делимость многочленов. Наибольший общий делитель. Алгоритм Евклида. Расширенный алгоритм Евклида.
- •Разложение рациональных функций в сумму дробей.
- •Неприводимый многочлен, его свойства
- •Из вытекает, либо , либо .
- •Если неприводимый многочлен делится на неприводимый многочлен, то они отличаются числовым множителем.
- •Корень многочлена.
- •Интерполяционный многочлен
- •Интерполяционный многочлен в форме Лагранжа
- •Интерполяционный многочлен в форме Ньютона
- •Разложение многочлена над полем рациональных чисел
- •Примитивный многочлен, его свойства
- •Критерий Эйзенштейна
- •Все коэффициенты многочлена f(X), кроме старшего, делятся на p
- •Старший коэффициент не делится на p
- •Свободный член не делится на
- •Метод Кронекера разложения многочлена на неприводимые многочлены над кольцом целых чисел.
- •Рациональные корни.
- •Присоединение корня. Поле разложения многочлена.
- •Формальная производная, ее свойства
- •Производные высоких порядков
- •Интерполяционный многочлен Лагранжа-Сильвестра
- •Формулы Виета
- •Симметрические полиномы
- •Формулы Кардано
- •Способ Феррари
- •Дискриминант
- •Основная теорема Алгебры
- •Разложение многочлена на неприводимые множители над полем вещественных чисел
- •Теорема Штурма
- •Любые два соседних многочлена не имеют общих корней
- •Последний многочлен не имеет вещественных корней.
- •Если в окрестностях корня a многочлена сам многочлен возрастает, то , а если убывает, то
- •Метод Гаусса решения системы линейных уравнений
- •Равносильные преобразования
- •Умножение строки не ненулевое число.
- •Перестановка строк
- •Прибавление к некоторой строке другой строки, умноженной на число.
- •Метод Гаусса.
- •Перестановки
- •Четность перестановок
- •Определитель
- •Свойства определителя
- •Изменит знак при перестановке столбцов
- •Равен нулю, если имеется два одинаковых столбца
- •Не изменится при прибавлении к столбцу другого столбца, умноженного на число.
- •Вычисление определителей произвольных порядков
- •Определитель Вандермонда
- •Теорема Лапласа
- •Умножение матриц
- •Формула Бине-Кощи
- •Операции с матрицами
- •Обратная матрица
- •Правило Крамера
- •Матрица элементарных преобразований
- •Построение обратной матрицы
- •Блочные матрицы
- •Алгоритм Штрассена
- •Кронекерово произведение
- •Формула Фробениуса
- •Линейные пространства.
- •. Линейная зависимость. Теорема о замене. Ранг системы.
- •Конечномерные пространства. Базис. Размерность. Дополнение до базиса. Базис суммы, пересечения.
- •. Прямая сумма подпространств. Проекция.
- •Изменение координат вектора при изменении базиса.
- •Изоморфизм линейных пространств.
- •Задание прямой и плоскости в пространстве. Деление отрезка. Задачи.
- •Ранги матрицы.
- •Общее решение системы линейных уравнений.
- •Двойственное пространство
- •Взаимное расположение линейных многообразий в пространстве.
- •Геометрия на плоскости и в пространстве.
- •Скалярное произведение.
- •Симметричность .
- •Векторное и смешанное произведение.
- •Уравнение прямой и плоскости в пространстве
- •Евклидово пространство. Скалярное произведение.
- •Изменение матрицы Грама при изменении базиса.
- •Ортогональность.
-
Алгоритм Штрассена
Использование правил блочного произведения
матриц позволяет уменьшить общее
количество операций, а значит, и время
выполнения работы программы. Допустим,
требуется умножить квадратные матрицы
A и B порядка
![]() .
При перемножении матриц, по формулам,
приведённым в определении произведения,
потребуется
.
При перемножении матриц, по формулам,
приведённым в определении произведения,
потребуется
![]() умножений и сложений. Разобьём матрицы
A и B на блоки
умножений и сложений. Разобьём матрицы
A и B на блоки
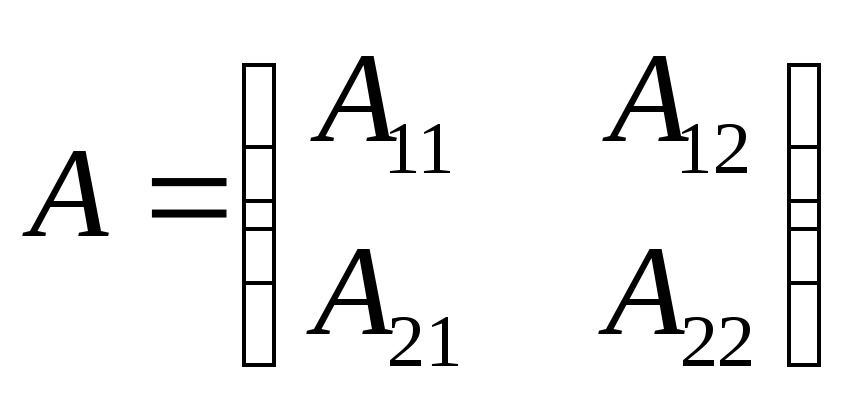
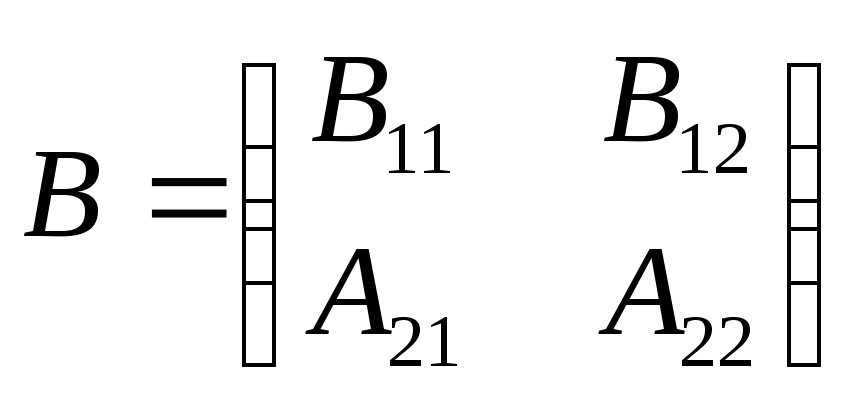 порядка n. Вычисление
произведения блочных матриц проведём
по формулам Штрассена
порядка n. Вычисление
произведения блочных матриц проведём
по формулам Штрассена
-
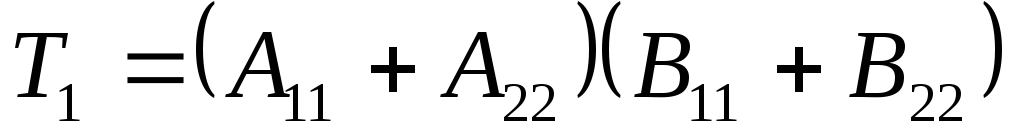 потребуется
потребуется
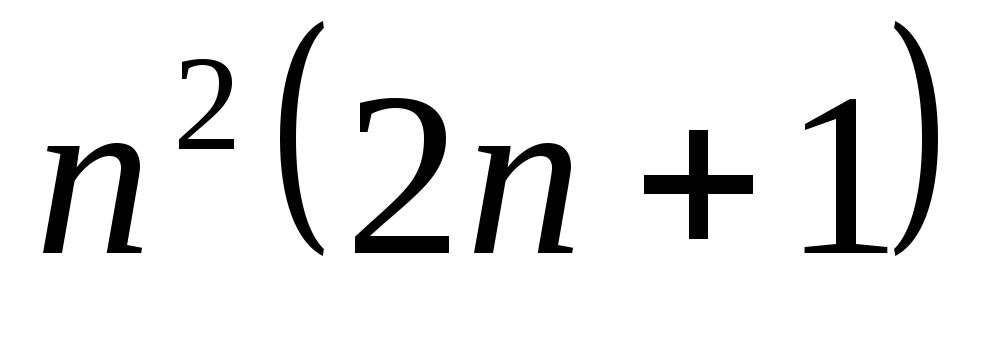 умножений и сложений
умножений и сложений -
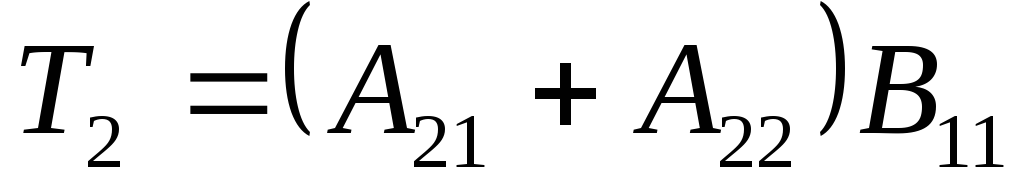 потребуется
потребуется
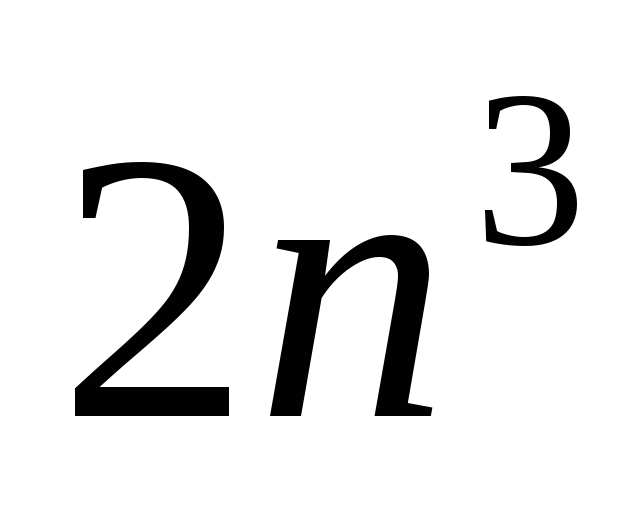 умножений и сложений
умножений и сложений -
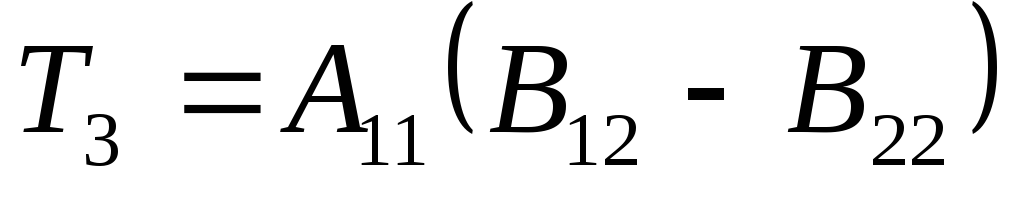 потребуется
потребуется
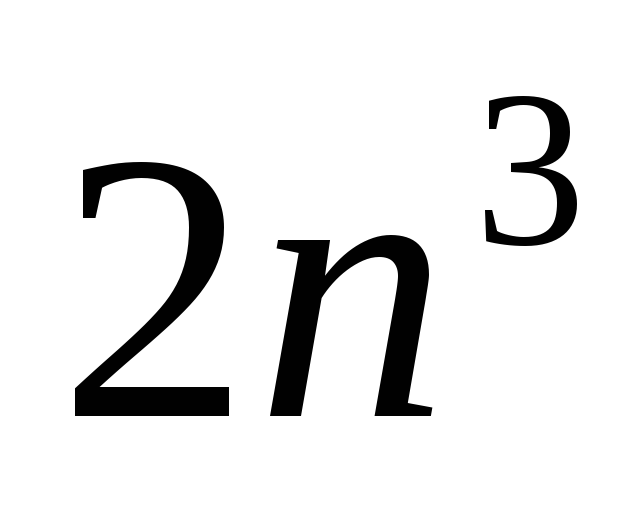 умножений и сложений
умножений и сложений -
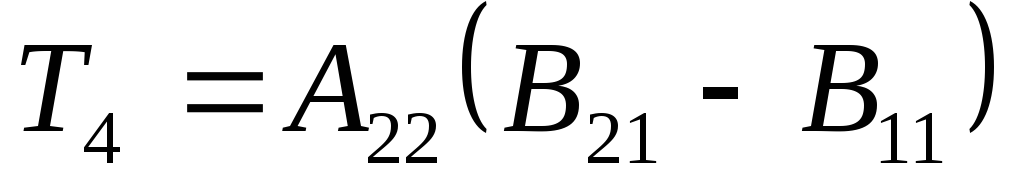 потребуется
потребуется
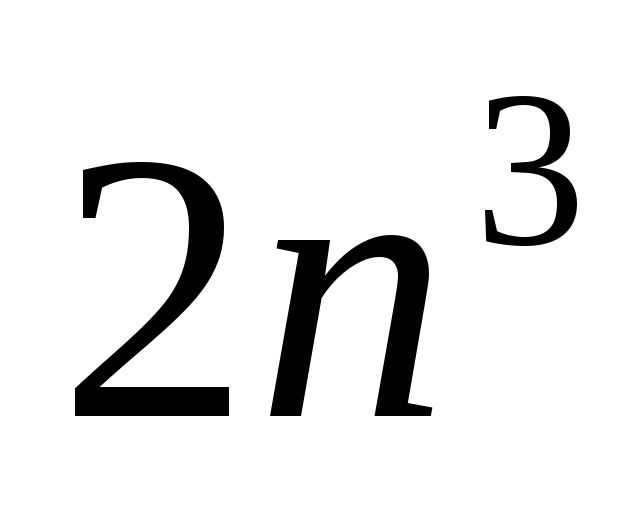 умножений и сложений
умножений и сложений -
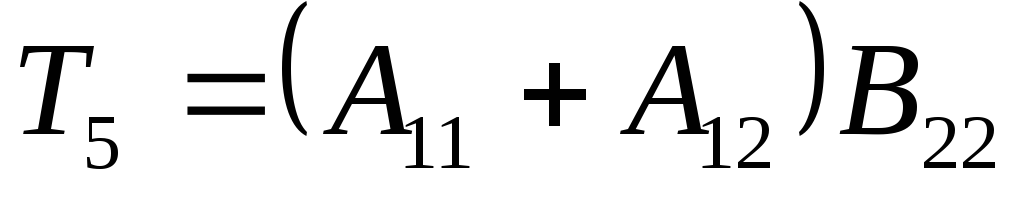 потребуется
потребуется
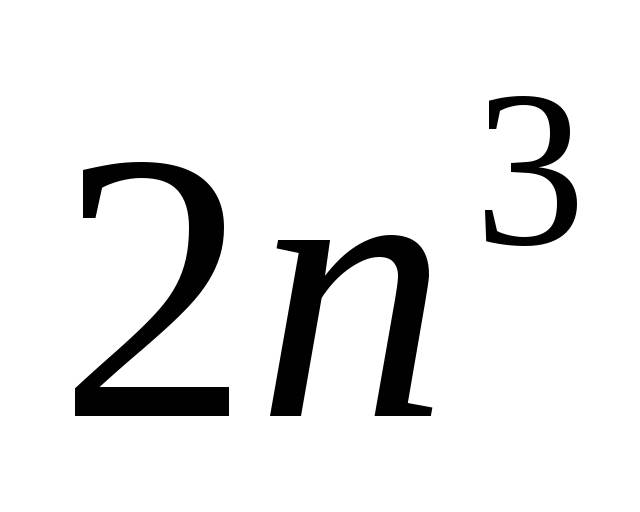 умножений и сложений
умножений и сложений -
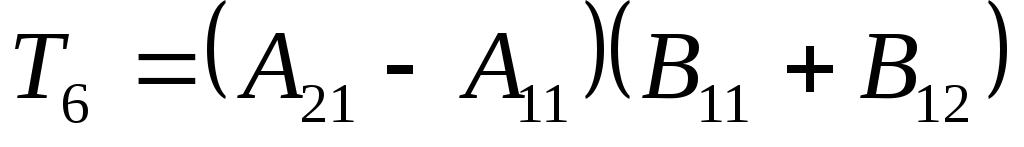 потребуется
потребуется
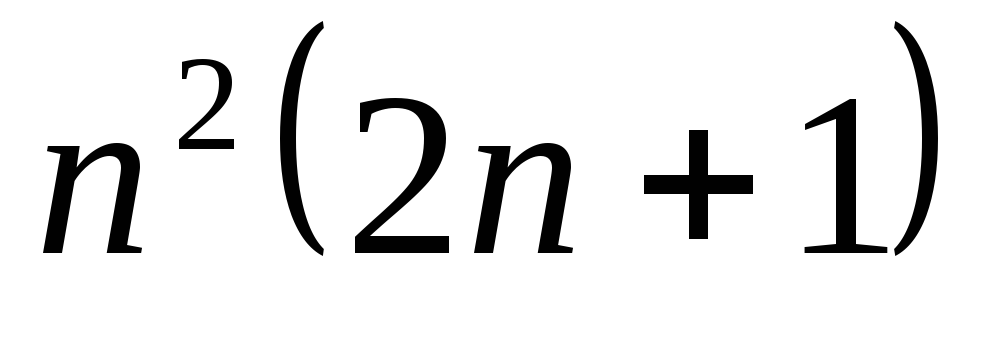 умножений и сложений
умножений и сложений -
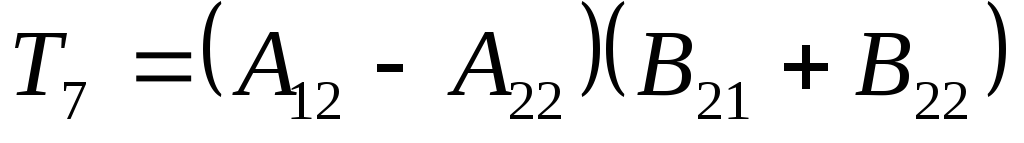 потребуется
потребуется
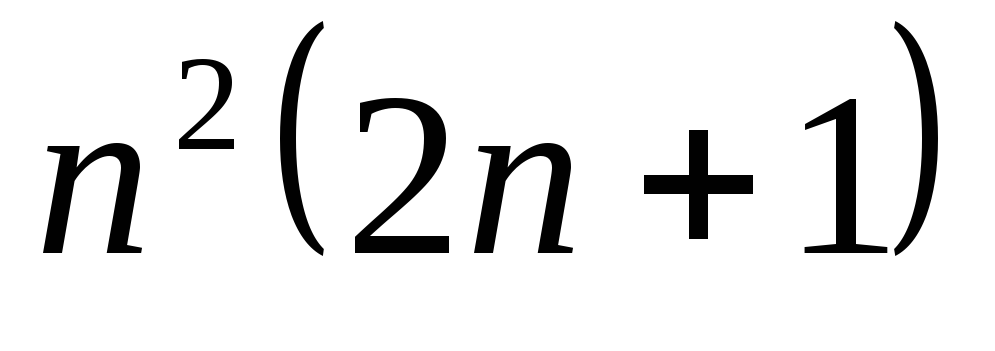 умножений и сложений
умножений и сложений -
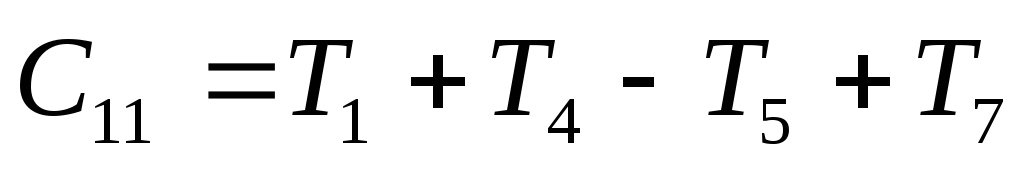 потребуется
потребуется
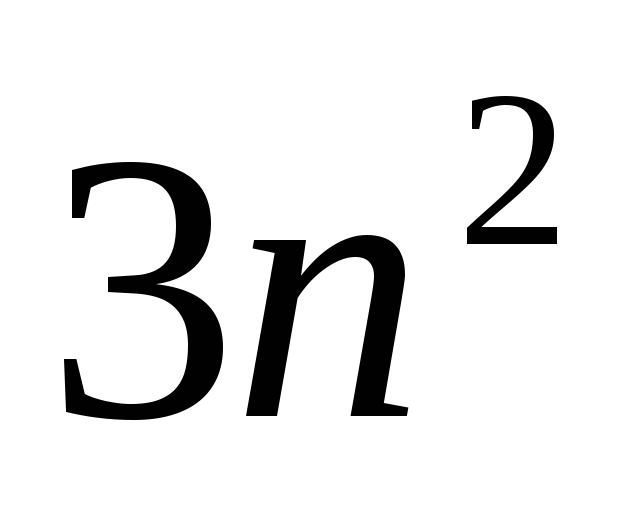 сложений
сложений -
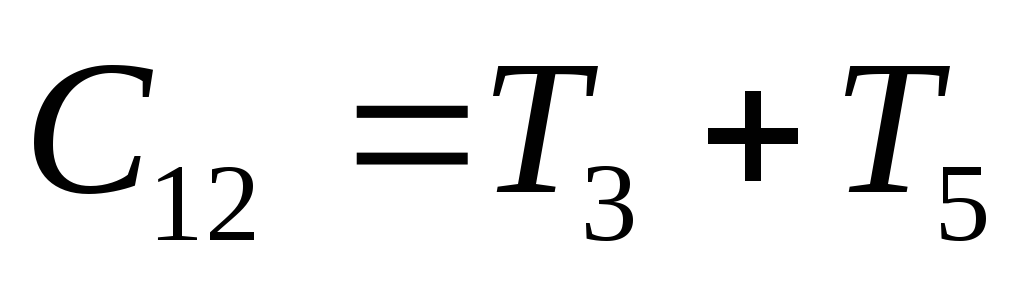 потребуется
потребуется
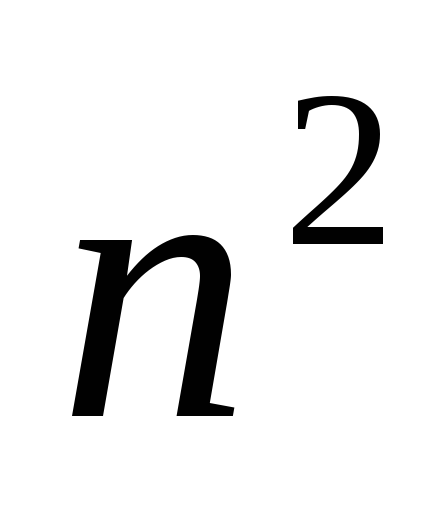 сложений
сложений -
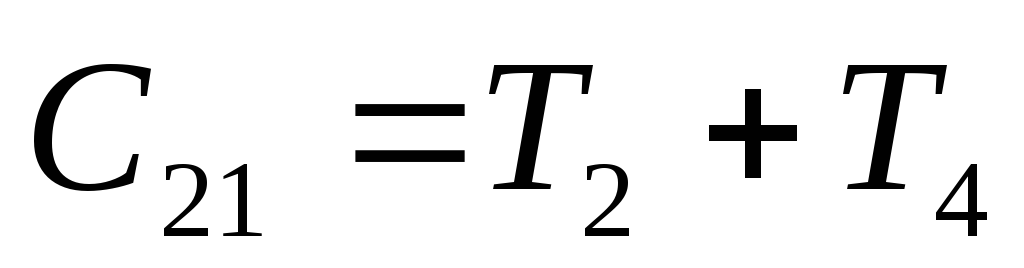 потребуется
потребуется
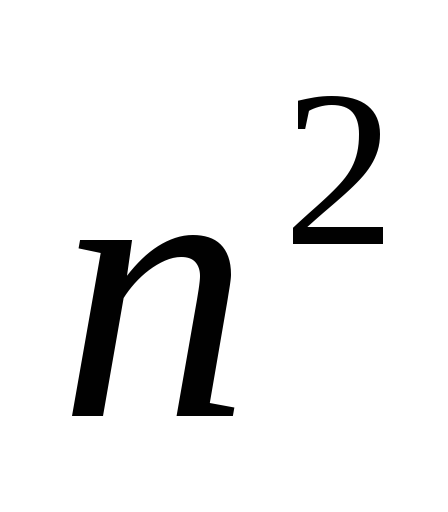 сложений
сложений -
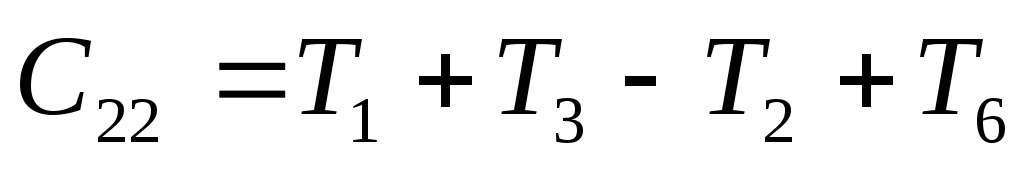 потребуется
потребуется
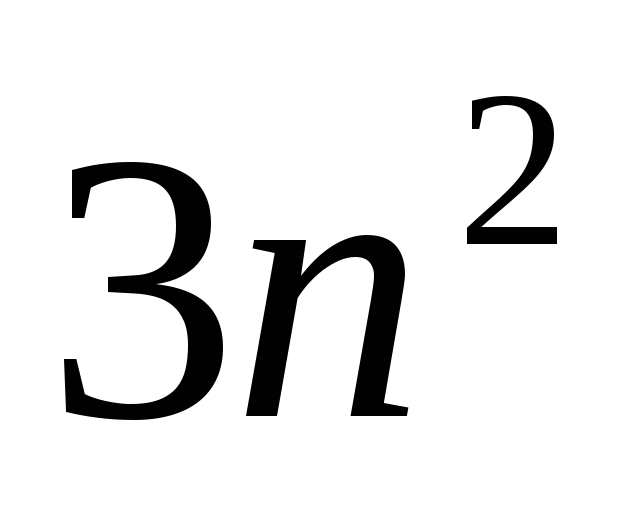 сложений.
сложений.
Всего, для вычисления произведения
матриц по формулам Штрассена, потребуется
![]() операций сложения и умножения. При
выполнении неравенства
операций сложения и умножения. При
выполнении неравенства
![]() (n>7) формулы Штрассена
приводят к меньшему объёму вычислений.
Выигрыш в числе операций будет
увеличиваться, если при вычислении
произведения матриц (шаги1-7) использовать
ту же схему.
(n>7) формулы Штрассена
приводят к меньшему объёму вычислений.
Выигрыш в числе операций будет
увеличиваться, если при вычислении
произведения матриц (шаги1-7) использовать
ту же схему.
Обозначим через
![]() число операций сложения и умножения,
используемых при умножении матриц n-го
порядка по формулам Штрассена. Справедлива
рекуррентная формула
число операций сложения и умножения,
используемых при умножении матриц n-го
порядка по формулам Штрассена. Справедлива
рекуррентная формула
![]() .
Положим
.
Положим
![]() .
Тогда
.
Тогда
![]()
![]() ,
далее, свернём сумму по формуле суммы
членов геометрической прогрессии и
заметим
,
далее, свернём сумму по формуле суммы
членов геометрической прогрессии и
заметим![]() .
В результате получим
.
В результате получим
![]() .
Подставив вместо k его
выражение через n (
.
Подставив вместо k его
выражение через n (![]() )
получим
)
получим
![]() (
(
![]() ).
).
-
Кронекерово произведение
Определение 6.22Пусть
![]() и
и
![]() - прямоугольные матрицы соответственно
размеров
- прямоугольные матрицы соответственно
размеров
![]() и
и
![]() .
Кронекеровым произведением
.
Кронекеровым произведением
![]() называется матрица
называется матрица
![]() размеров
размеров
![]() следующего блочного строения
следующего блочного строения
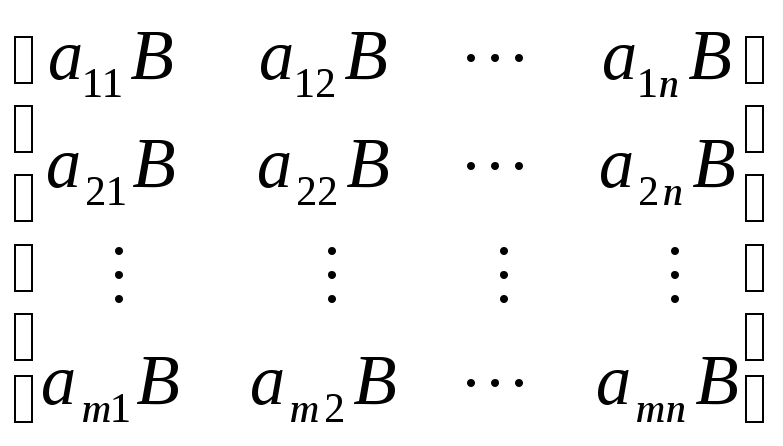 .
.
Приведем основные свойства кронекерова произведения матриц.
Свойство 6.16. Пусть
![]() и
и
![]() ,
тогда
,
тогда
![]() .
.
Доказательство следует из правила блочного произведения матриц.
Свойство 6.17. Пусть
существуют
![]() и
и
![]() ,
тогда
,
тогда
![]() .
.
Доказательство. По доказанному
ранее (Свойство 6 .16), имеем
![]() .
Из полученного равенства вытекает
требуемое утверждение.
.
Из полученного равенства вытекает
требуемое утверждение.
Свойство 6.18.
![]() .
.
Доказательство следует из определения операций кронекерова произведения и транспонирования матриц.
Свойство 6.19. Пусть
![]() - квадратная матрица порядка
- квадратная матрица порядка
![]() ,
а
,
а
![]() - квадратная матрица порядка
- квадратная матрица порядка
![]() ,
тогда
,
тогда
![]() .
.
Доказательство. Если матрица A
имеет верхний треугольный вид, то
утверждение получается последовательным
разложением определителя по теореме
Лапласа по первым m
столбцам. Если матрица A
имеет нижний треугольный вид, то
утверждение получается последовательным
разложением определителя по теореме
Лапласа по первым m строкам.
Рассмотрим случай, когда матрица A
не треугольная. Элементарными
преобразованиями со строками (а именно,
перестановкой строк и прибавлением к
одной строки, другой строки умноженной
на число) приведём матрицу A
к треугольному виду T.
Тогда
![]() ,
где
,
где
![]() - матрица элементарных преобразований.
Имеет место равенство
- матрица элементарных преобразований.
Имеет место равенство
![]() ,
из которого выводим
,
из которого выводим
![]() .
Поскольку T – треугольная
матрица, то
.
Поскольку T – треугольная
матрица, то
![]() .
Матрица элементарного преобразования
.
Матрица элементарного преобразования
![]() ,
если она соответствует прибавлению к
некоторой строке другой строки, умноженной
на число, имеет треугольный вид, и, значит
,
если она соответствует прибавлению к
некоторой строке другой строки, умноженной
на число, имеет треугольный вид, и, значит
![]() .
Если матрица элементарного преобразования
.
Если матрица элементарного преобразования
![]() соответствует перестановке двух строк,
то
соответствует перестановке двух строк,
то
![]() .
Таким образом,
.
Таким образом,
![]() .
Для доказательства утверждения осталось
заметить равенство
.
Для доказательства утверждения осталось
заметить равенство
![]() .
.
Следствие 6.14.
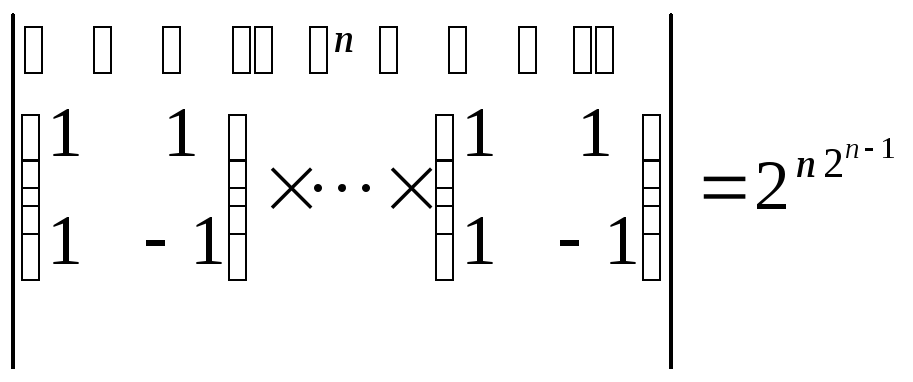 .
.
Доказательство
проведём индукцией по n.
Положим
![]() и
и
![]() .
При n=2
имеем
.
При n=2
имеем
![]() ,
т.е. утверждение верно. Пусть оно
справедливо при n-1.
Тогда
,
т.е. утверждение верно. Пусть оно
справедливо при n-1.
Тогда
![]() ,
что и требовалось доказать.
,
что и требовалось доказать.
