3. Определитель Вандермонда

Пусть даны числа . Матрицей Вандермонда называется матрица, у которой на пересечении i-го столбца и j-ой строки расположен элемент, равный . Обозначим через матрицу Вандермонда. Определитель матрицы Вандермонда является многочленом от , т.к. . Рассмотрим определитель как многочлен от . Степень этого многочлена равна n-1, а его корни равны (т.к. определитель матрицы с двумя одинаковыми строками равен нулю). Следовательно, , где q – коэффициент при старшей степени. Легко убедиться, что 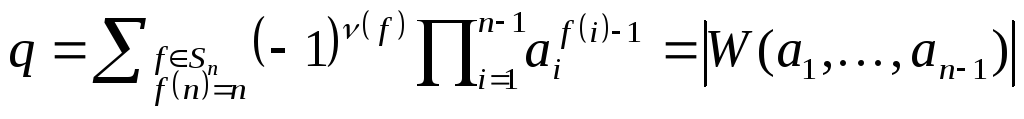. Таким образом получена рекуррентная формула , последовательным применением которой придём к равенству .

4. Теорема Лапласа

Определение 5.18. Пусть и множества номеров строк и столбцов матрицы A, соответственно. Подматрицу матрицы A, расположенную на пересечении строк с номерами из I и столбцов с номерами из J, обозначим как , а подматрицу, получаемую из A, вычеркиванием строк с номерами из I и столбцов с номерами из J обозначим через . Определитель называется минором, а определитель - дополнительным минором.

Лемма 5.11 Справедливо равенство .

Доказательство. Выразим правую часть равенства через элементы исходной матрицы. Для этого заметим, что и , где 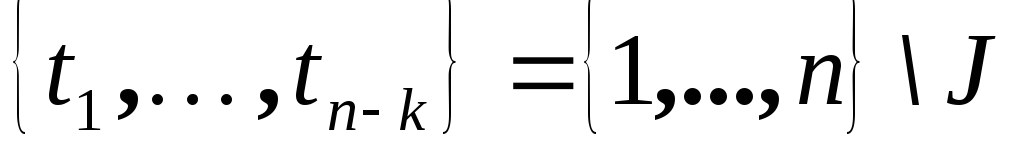(номера упорядочены в порядке возрастания). Подставим данные выражения в правую часть и перемножим

Первая сумма состоит из слагаемых, вторая сумма – из k! слагаемых и третья сумма – (n-k)! слагаемых. Следовательно, общее количество слагаемых равно n!. Покажем, что каждое из этих слагаемых входит в определитель с тем же самым знаком. Слагаемое имеет вид , где . В определителе оно соответствует перестановке . Представим перестановку в виде произведения трёх перестановок , где , и . Легко убедиться в справедливости равенств , , . Следовательно, , и таким образом, совпадение знаков показано, что завершает доказательство леммы.

Теорема 5.31 (Лапласа). Пусть множество номеров строк. Справедливо равенство .

Доказательство. Обозначим через B матрицу, получающуюся из матрицы A последовательной перестановкой строк с номерами из I на место первых k строк (при этом порядок остальных строк не нарушается). Для этого потребуется перестановок строк, и значит, . Разложив определитель матрицы B (Лемма 5 .11), и заметив, что 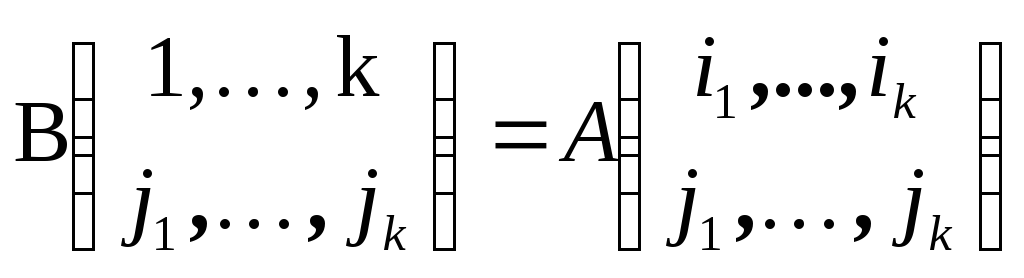, 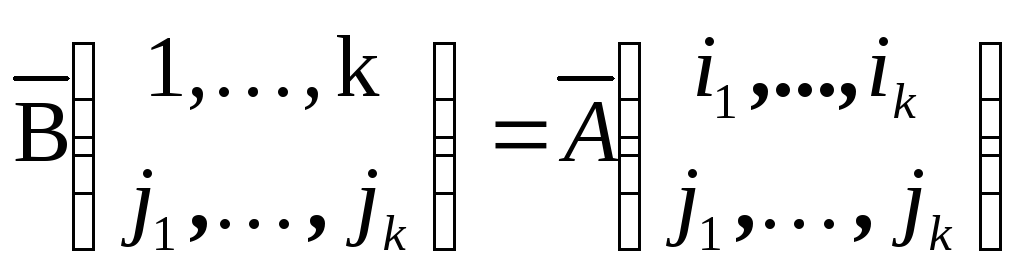выводим .

Следствие 5.9. Пусть множество номеров столбцов. Справедливо равенство .

Вытекает из теоремы Лапласа и равенства определителей .

Следствие 5.10. (разложение по столбцу). Пусть j – номер столбца. Справедливо равенство .

Следствие 5.11 (разложение по строке) Пусть i – номер строки. Справедливо равенство .

Примеры использования теоремы Лапласа.

5. Умножение матриц

Определение 5.19. Пусть A матрица размерами m*n, а B матрица размерами n*k. Произведением матриц A*B называется матрица C размерами m*k, элементы которой находятся по формулам . Другими словами, элемент матрицы произведения, расположенный на пересечении i-ой строки и j-го столбца равен произведению i-ой строки A на j-ый столбец B.

Свойство 5.12 Пусть A*B=C. Строка i матрицы C является комбинацией строк матрицы B, причём коэффициенты берутся из i строки матрицы A. Столбец j матрицы C является комбинацией столбцов матрицы A, причём коэффициенты берутся из j столбца матрицы B.

Свойство 5.13. Произведение матриц не коммутативно.

Свойство 5.14. Произведение матриц ассоциативно.