2.4.3 Основные законы распределения случайных погрешностей

Закон равномерной плотности. Если возможные значения погрешностей заключены в определенных пределах и одинаково вероятны, то считается, что они распределены по закону равномерной плотности (рис. 1.7).

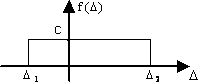
Рис 1.7

Плотность вероятности определяется

,

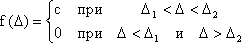где .

Числовые характеристики погрешностей будут равны:

где [], [] – математическое ожидание и СКО погрешности,  и  – её предельные значения. Если распределение симметрично (т.е.

, то []=0, []=.

Нормальный закон распределения (закон Гаусса). Нормальный закон распределения погрешностей описывается формулой

.

На рис. 1.8 показан вид нормального закона для двух значений СКО, причем s₂>s₁. Т.к. =-, то закон распределения случайной составляющей погрешности () имеет тот же вид и описывается аналогичным соотношением (рис. 1.9)

.

Рис. 1.8

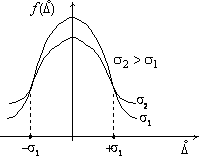
Рис. 1.9

,

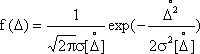где  - СКО случайной погрешности (=).

Широкое распространение нормального закона объясняется тем, что рассеивание значений погрешностей вызывается множеством случайных факторов. Нормальный закон представляет собой симметричную кривую. Анализируя формулу и графики для нормального закона распределения, можно сделать следующие выводы:

1. Случайные погрешности, одинаковые по величине, но различные по знаку имеют одинаковую плотность вероятности т.е. встречаются одинаково часто (аксиома симметрии);

2. Малые случайные погрешности имеют большее значение (), т.е. встречаются чаще, чем большие (аксиома монотонного убывания плотности вероятности случайной погрешности);

3. Точка перегиба функции () по оси абсцисс соответствует значению случайной погрешности, равной СКО (±).

Так как значение  определяется через истинное значение измеряемой величины, которые не известно, то по этой же причине нельзя определить и СКО. Для практического использования приведенных соотношений необходимо принять какое-то значение измеряемой величины за истинное. В качестве такого значения принимается среднее арифметическое значение ряда измерений величины , полученное из формулы

,

где  - среднее арифметическое ряда измерений;  - -ый результат измеряемой величины из ряда , ,…,  (выборки); – число измерений в ряде (объём выборки).

Зная среднее арифметическое, можно определить значение остаточных погрешностей (случайных отклонений)

.

При достаточно большом числе измерений (®∞),  ,®.

Правильность подсчета  и  проверяют, используя свойство остаточных погрешностей .

При принятых допущениях для определения точности ряда измерений вычисляют оценку СКО  по формуле Бесселя, которую называют средним квадратическим отклонением ряда измерений:

.

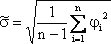Для данной серии из  измерений среднее арифметическое  является функцией результатов отдельных измерений , ,…, . Если провести новую серию из  измерений, то вследствие влияния отдельных факторов на результаты измерений значения  второй серии будут отличаться от  первой серии. Следовательно, новое значение  и  будут другим. Поэтому , получаемое в одной серии измерений (из одной выборки) является случайным приближением к . Величина получаемого при этом разброса значений  и  определяется с помощью оценки среднеквадратического отклонения среднего арифметического, которое можно определить по формуле

.

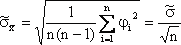Полученные таким образом оценки ,, называются точечными. Термин “оценка” обозначает, что полученные результаты ,, получены по результатам ограниченной выборки объёмом n из генеральной совокупности, для которой предполагается, что n ®∞. Среднее квадратическое отклонение среднего арифметического также называется средним квадратическим отклонением результата измерений.

Шумы

Цвета шума — система терминов, приписывающая некоторым видам шумовых сигналов определённые цвета исходя из аналогии между спектром сигнала произвольной природы (точнее, его спектральной плотностью или, говоря математически, параметрами распределения случайного процесса) и спектрами различных цветов видимого света. Эта абстракция широко используется в отраслях техники, имеющих дело с шумом (акустика, электроника, физика и т. д.).

Многие из следующих определений рассматривают спектр сигнала на всех частотах.

\ Основные «цвета» шумов

Цветовые соответствия различных типов шумового сигнала определяются с помощью графиков (гистограмм) спектральной плотности, то есть распределения мощности сигнала по частотам.