Корреляционная Таблица.
|
Интервалы xi |
Интервалы yi |
Число наблюдений mi |
Среднее значение в данном интервале по xi |
||||||
|
7,382- 9,7492* |
9,7492- 12,1164 |
12,1164- 14,4836 |
14,4836- 16,8508 |
16,8508- 19,218 |
|
|
|||
|
2,412-3,4016* |
7,382
|
|
|
|
|
1 |
7,382 |
||
|
3,4016-4,3912 |
|
11,367 10,108 11,688 10,919 |
|
|
|
4 |
9,497 |
||
|
4,3912-5,3808 |
|
|
13,036 13,132 |
15,103 16,522 |
17,253 |
5 |
15,009 |
||
|
5,3808-6,3704 |
|
|
14,167
|
15,847 14,886 15,067 15,66 16,259 16,261 |
|
7 |
15,450 |
||
|
6,3704-7,36 |
|
|
|
16,737 15,563 15,991 |
17,692 17,124 16,961 16,825 17,2 17,99 19,218 17 19,059 17,114 |
13 |
17,267 |
||
|
Число наблюдений |
1 |
4 |
3 |
11 |
11 |
30 |
5 |
||
*-верхняя граница включительно.
По корреляционной таблице можно судить о характере связи. В данном случае зависимость прямая.
Графической формой систематизации данных наблюдений является поле корреляции, представляющее собой точечный график, где по оси абсцисс откладываются значения факторного признака, а по оси ординат – результативного.
Зависимость производительности труда (выпуск товаров и услуг на одного работника) от уровня вооруженности труда ОПФ (стоимость ОПФ на одного работника) показана на рисунке 5.
Расчет эмпирической линии регрессии при прямолинейной зависимости выполняется по уравнению:
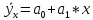
Система «нормальных» уравнений при выравнивании по прямой имеет вид:
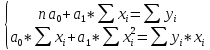
Найдем
значения
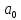и
:
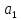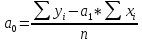
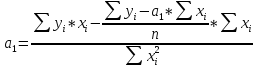
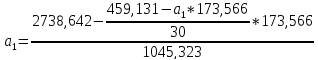
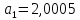
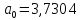
Следовательно, получается:
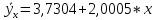
Таблица 14.
Вспомогательная таблица для расчёта сумм слагаемых в системе уравнений.
|
№ n/n |
xi |
yi |
xi2 |
yi2 |
yi*xi |
|
|
1 |
2,412 |
7,382 |
5,818 |
54,494 |
17,805 |
8,557 |
|
2 |
4,014 |
10,108 |
16,112 |
102,172 |
40,574 |
11,760 |
|
3 |
4,216 |
10,919 |
17,775 |
119,225 |
46,035 |
12,165 |
|
4 |
4,253 |
11,367 |
18,088 |
129,209 |
48,344 |
12,239 |
|
5 |
4,260 |
11,688 |
18,148 |
136,609 |
49,791 |
12,253 |
|
6 |
4,480 |
17,253 |
20,070 |
297,666 |
77,293 |
12,693 |
|
7 |
4,643 |
13,036 |
21,557 |
169,937 |
60,526 |
13,019 |
|
8 |
5,128 |
15,103 |
26,296 |
228,101 |
77,448 |
13,989 |
|
9 |
5,158 |
13,132 |
26,605 |
172,449 |
67,735 |
14,049 |
|
10 |
5,326 |
16,522 |
28,366 |
272,976 |
87,996 |
14,385 |
|
11 |
5,531 |
16,259 |
30,592 |
264,355 |
89,929 |
14,795 |
|
12 |
5,595 |
14,167 |
31,304 |
200,704 |
79,264 |
14,923 |
|
13 |
5,711 |
15,660 |
32,616 |
245,236 |
89,434 |
15,155 |
|
14 |
5,763 |
15,847 |
33,212 |
251,127 |
91,326 |
15,259 |
|
15 |
5,909 |
14,886 |
34,916 |
221,593 |
87,961 |
15,551 |
|
16 |
6,087 |
16,261 |
37,052 |
264,420 |
98,981 |
15,907 |
|
17 |
6,171 |
15,067 |
38,081 |
227,014 |
92,978 |
16,075 |
|
18 |
6,591 |
16,737 |
43,441 |
280,127 |
110,314 |
16,916 |
|
19 |
6,644 |
19,059 |
44,143 |
363,245 |
126,628 |
17,022 |
|
20 |
6,672 |
15,991 |
44,516 |
255,712 |
106,692 |
17,078 |
|
21 |
6,676 |
15,563 |
44,569 |
242,207 |
103,899 |
17,086 |
|
22 |
6,680 |
17,990 |
44,622 |
323,640 |
120,173 |
17,094 |
|
23 |
6,708 |
17,692 |
44,997 |
313,007 |
118,678 |
17,150 |
|
24 |
6,717 |
17,000 |
45,118 |
289,000 |
114,189 |
17,168 |
|
25 |
6,903 |
17,124 |
47,651 |
293,231 |
118,207 |
17,540 |
|
26 |
6,903 |
19,218 |
47,651 |
369,332 |
132,662 |
17,540 |
|
27 |
6,913 |
16,961 |
47,790 |
287,676 |
117,251 |
17,560 |
|
28 |
6,914 |
17,114 |
47,803 |
292,889 |
118,326 |
17,562 |
|
29 |
7,228 |
16,825 |
52,244 |
283,081 |
121,611 |
18,190 |
|
30 |
7,360 |
17,200 |
54,170 |
295,840 |
126,592 |
18,454 |
|
Итого: |
173,566 |
459,131 |
1045,323 |
7246,274 |
2738,642 |
459,134 |
Оценка тесноты корреляционной связи осуществляется с помощью линейного коэффициента корреляции (r) и корреляционного отношения (Rэ).
Линейный коэффициент корреляции рассчитывается по формуле:
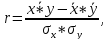
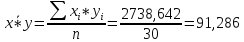
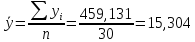
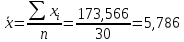
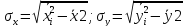
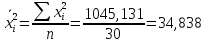
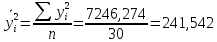
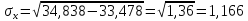
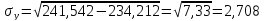
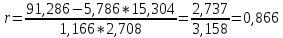
Т.к. r = 0,868, то связь является прямой и зависимость между X и Y довольно тесная.
Оценка значимости линейного коэффициента корреляции осуществляется по формуле:
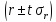с
вероятностью P.
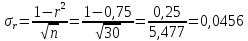
Коэффициент корреляции Rэ является универсальным измерителем тесноты связи. Если r можно использовать только при линейной корреляции, то Rэ применяется при любой форме связи (при линейной связи r = Rэ).
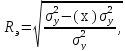
где
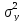- дисперсия фактора Y;
-
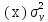дисперсия Y под действием
всех факторов, кроме X.
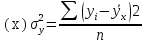
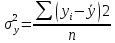
Таблица 15.