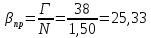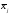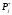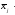3 Расчетное прогнозирование полных отказов и показателей долговечности рельсов
3.1 Расчет среднестатистической и максимально вероятной осевых нагрузок ,
Результаты измерений осевых нагрузок зафиксированы в задании на курсовой проект в порядке их поступления. Так, например, получены следующие результаты измерений осевых нагрузок от грузового подвижного состава, тс/ось:
Таблица 3.1 Простая статическая совокупность сил, измеренных на участке
|
8 |
12 |
27 |
19 |
19 |
24 |
22 |
24 |
|
10 |
15 |
24 |
19 |
17 |
23 |
20 |
24 |
|
14 |
14 |
22 |
18 |
20 |
21 |
16 |
18 |
|
13 |
30 |
23 |
23 |
18 |
11 |
15 |
24 |
|
15 |
29 |
21 |
21 |
22 |
15 |
16 |
16 |
|
12 |
28 |
16 |
21 |
22 |
14 |
22 |
16 |
|
13 |
27 |
16 |
21 |
9 |
32 |
19 |
18 |
|
16 |
27 |
24 |
21 |
10 |
29 |
19 |
16 |
|
19 |
28 |
25 |
18 |
13 |
26 |
20 |
16 |
|
18 |
24 |
22 |
18 |
13 |
26 |
18 |
14 |
Полученные значения случайной величины называются простой статистической совокупностью.
3.1.1 Обработка результатов измерений
Для того, чтобы установить закономерность исследуемой величины и ее характеристики, простая статистическая совокупность подвергается обработке, которая заключается в следующем.
1. Все данные располагаются в порядке возрастания или убывания значений случайной величины. Получается так называемый вариационный ряд.
Например, данные приведенного выше примера можно расположить в порядке возрастания нагрузки:
Таблица 3.1 Простая статическая совокупность сил, измеренных на участке, расположенная в порядке возрастания нагрузки
|
8 |
13 |
16 |
18 |
19 |
21 |
23 |
26 |
|
9 |
14 |
16 |
18 |
19 |
21 |
24 |
27 |
|
10 |
14 |
16 |
18 |
19 |
22 |
24 |
27 |
|
10 |
14 |
16 |
18 |
20 |
22 |
24 |
27 |
|
11 |
14 |
16 |
18 |
20 |
22 |
24 |
28 |
|
12 |
15 |
16 |
18 |
20 |
22 |
24 |
28 |
|
12 |
15 |
16 |
18 |
21 |
22 |
24 |
29 |
|
13 |
15 |
16 |
19 |
21 |
22 |
24 |
29 |
|
13 |
15 |
17 |
19 |
21 |
23 |
25 |
30 |
|
13 |
16 |
18 |
19 |
21 |
23 |
26 |
32 |
В вариационном ряде просматривается закономерность случайной величины. Однако при большом числе измерений (порядка сотен) такая форма записи статистических данных становиться громоздкой и мало наглядной.
2. По вариационному ряду в каждом разряде подсчитывается число наблюдений (частоты), а затем определяются значения частостей:
,
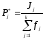(3.1.)
где
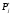– частость, выражает статистическую
вероятность того, что случайная величина
окажется в j-ом разряде;
Jj – частота или число наблюдений в j-ом разряде;
j – номер разряда;
k – число разрядов.
3. Полученные значения разрядов, частот и частостей оформляется в виде статистического ряда, вид которого для рассматриваемой на примере простой статистической совокупности приведен в таблице 3.3.
Таблица 3.3 Характеристики простой статистической совокупности
|
№ разряда |
Значения промежутков в разряде xjH - xjB |
|
Частота fj |
Частость
|
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
1 |
[8;12) |
9,5 |
5 |
0,0625 |
0,59375 |
5,640625 |
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
2 |
[12;16) |
13,5 |
14 |
0,175 |
2,3625 |
31,89375 |
|
3 |
[16;20) |
17,5 |
24 |
0,3 |
5,25 |
91,875 |
|
4 |
[20;24) |
21,5 |
18 |
0,225 |
4,8375 |
104,0063 |
|
5 |
[24;28) |
25,5 |
13 |
0,1625 |
4,14375 |
105,6656 |
|
6 |
[28;32] |
30 |
6 |
0,075 |
2,25 |
67,5 |
|
Итого |
|
|
80 |
1 |
19,4375 |
406,5813 |
В таблице 3.3
обозначают соответственно нижнюю и
верхнюю границы j-го
разряда. Частость (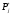
),
например, для первого разряда
статистического ряда (таблица 3.1) будет
равна
, (3.2)
4. Для
наглядности статистическое распределение
случайной величины часто изображается
в виде гистограммы, которая представляет
собой графическое изображение
статистического ряда и строиться
следующим образом: по оси абсцисс
откладываются значения интервалов
разрядов (Δ xj)
и на каждом из них строиться прямоугольник,
площадь которого равна частости (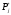
).
Тогда высота прямоугольника (Δ
уj) будет равна
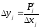, (3.3)
Соединив середины верхних сторон прямоугольников, получим многоугольник распределения случайной величины.
В качестве примера на рис. 3.3 приведены гистограмма и многоугольник распределения по данным статистического ряда (таблица 3.3).
5. По данным статистического ряда определяются числовые характеристики простой статистической совокупности:
-
Первый начальный момент или статистическое среднее:
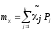(3.4) (3.4)
где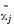 
- среднее значение случайной величины
в j-ом разряде статистического
ряда
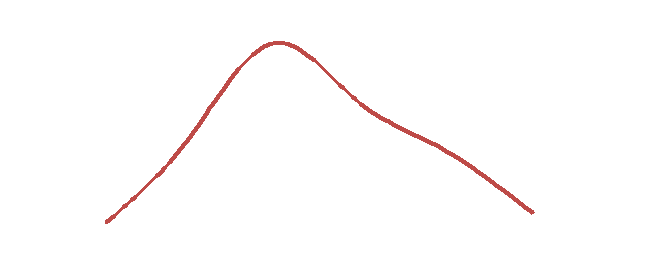
Рисунок 3.1 Гистограмма и многоугольник распределения по данным статического ряда
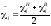(3.5) (3.5)
б. Статистическая дисперсия
,
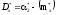(3.6) (3.6)
где 
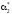- статистический второй начальный
момент,
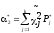(3.7.) (3.7)
в. Статистическое среднее квадратическое отклонение
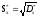(3.8) (3.8)
г. Максимальная вероятностная осевая нагрузка
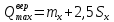, (3.9)
д. Отказы рельсов от пропущенного тоннажа и осевой нагрузки
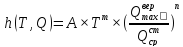(3.10) (3.10)
где T – наработка тоннажа, млн. т. брутто, ∆Т=25 млн.т брутто
А – для рельсов Р65, прямого участка А=3,9·10-5, кривого участка А=4,0·10-5
Вычисление числовых характеристик удобно производить, пользуясь табличной схемой, приведенной в таблице 3.3 (для рассматриваемого примера).
Из таблицы 3.3 следует, что числовые характеристики рассматриваемой простой статистической совокупности будут следующими:
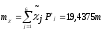
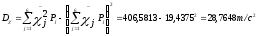
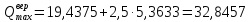
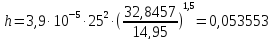
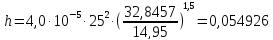
Таблице 3.4. Значения зависимости пропущенного тоннажа от осевой нагрузки
|
T |
выход рельсов, прямая |
выход рельсов, кривая |
|
25 |
0,053553 |
0,054926 |
|
50 |
0,214211 |
0,219704 |
|
75 |
0,481975 |
0,494334 |
|
100 |
0,856845 |
0,878815 |
|
125 |
1,33882 |
1,373149 |
|
150 |
1,927901 |
1,977334 |
|
175 |
2,624087 |
2,691371 |
|
200 |
3,427379 |
3,515261 |
|
225 |
4,337777 |
4,449002 |
|
250 |
5,35528 |
5,492595 |
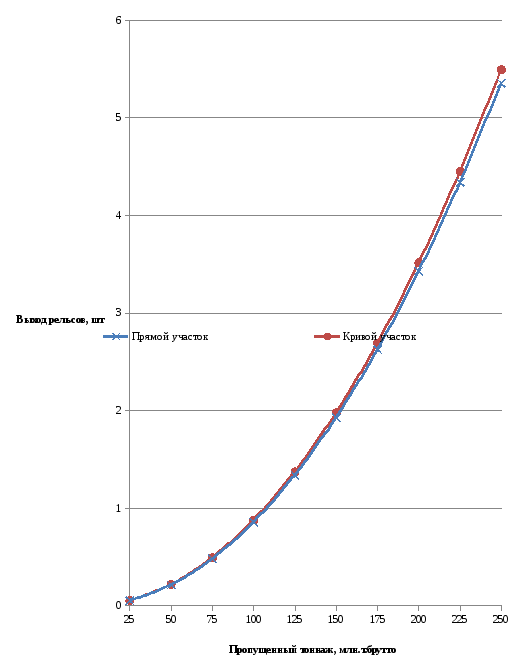
Рисунок 3.2. График зависимости выхода рельсов от пропущенного тоннажа.
Как видно из расчетов, при заданных условиях эксплуатации число одиночных отказов рельсов приблизится к допускаемому при наработке тоннажа в 250 млн т брутто, причем как в прямом так и в кривом участке пути. Это можно объяснить тем, что рельсы типа Р65 способны нормально воспринимать нагрузку в обоих случаях в отличие например от рельсов типа Р50, в случае которых выход быстрее происходит в кривой т.к., действует большая нагрузка при проходе подвижного состава, по сравнению с рельсами, уложенными в прямом участке, а также большими внутренними напряжениями, вызванных особенностями условий эксплуатации.
Определение наработки тоннажа при котором количество отказов рельсов будет равно допускаемому:
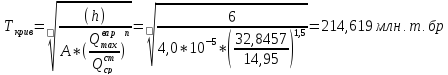
Ресурс в годах между капитальными ремонтами:
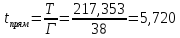
Количество одиночных отказов рельсов за последний год пред капитальным ремонтом пути:
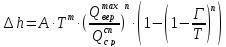(3.11) (3.11)
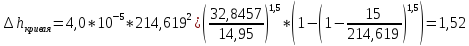
Таким образом, при заданных условиях эксплуатации, необходимость сплошной замены верхнего строения пути возникнет в прямом участке через 5,7 лет эксплуатации, после пропуска 217,353 млн т брутто тоннажа, причем за последний год перед капитальным ремонтом пути количество одиночых отказов рельсов составит 1,5 шт/км; в кривом – через 5,6 лет, при наработке тоннажа 214,619 млн т бр, одиночный выход рельсов составит 1,52 шт/км.
Параметр потока отказов составит:
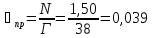
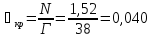
Средняя наработка на отказ будет равна:
