
- •Введение
- •1 Оценка надежности конструкции верхнего строения пути
- •Показатели надежности и модели отказов элементов верхнего строения пути
- •Оценка и прогнозирование надежности рельсов
- •Определение параметров нормального распределения
- •Прогнозирование отказов рельсов
- •Оценка надежности рельсовых скреплений
- •1.4 Оценка надежности подрельсовых оснований
- •1.5 Оценка надежности состояние балластного слоя
- •2 Управление надежностью бесстыкового пути
- •3 Расчетное прогнозирование полных отказов и показателей долговечности рельсов
- •3.1 Расчет среднестатистической и максимально вероятной осевых нагрузок ,
- •3.1.1 Обработка результатов измерений
- •Выравнивание статистических рядов
- •3.3 Алгоритм построения статистического ряда и определения его числовых характеристик
- •Список литературы
1.4 Оценка надежности подрельсовых оснований
Шпалы, эксплуатирующиеся примерно в равных условиях, при одинаковых объемах перевозок отказывают в различное время вследствие существующего разброса прочностных свойств древесины, качества обработки антисептиками, условий опирания шпал в балласте, наличия неровностей на поверхности катания рельсов, в том числе стыков. Следовательно, повреждение шпал – случайный процесс, а пропущенный тоннаж до отказа шпал – случайная величина.
Применение модели нормального распределения обусловлено следующим: отказы шпал вызываются многими факторами, каждый из которых оказывает определенное воздействие на развитие дефектов, теоретическое распределение должно иметь монотонно возрастающую функцию интенсивности отказов, так как известно, что с ростом наработки повышается интенсивность отказов.
Исходная информация об отказах шпал собирается по ведомостям покилометрового учета замененных шпал и отчетам о наличии в пути негодных шпал. При проведении статистических экспериментов выполняется следующее условие: данные об отказах шпал собираются на участках, характеризующихся определенным набором признаков (грузонапряженность, нагрузки на ось, скорость движения поездов, тип верхнего строения, план и профиль).
Результаты статистической выборки данных об отказах шпал приведены в таблице 1.7, где представлен сгруппированный ряд, полученный по результатам статистического эксперимента на участке железной дороги (грузонапряженность 38 млн. т брутто, средняя сетевая нагрузка 14,95 тс, рельсы типа Р65 длиной 25 м, балласт щебеночный).
При построении сгруппированного ряда весь диапазон наработки 0…645 млн. т брутто был разделен на интервалы. Для каждого интервала подсчитывалась частота отказов шпал R(ti) нарастающим итогом.
По частоте определялось значение частости
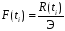 ,
(1.46)
,
(1.46)
где Э – средняя эпюра шпал (для рассматриваемого участка Э = 1908 шп/км).
Эмпирический квантиль UPi наблюдался по частости F(ti) с использованием табулированных значений функций (прил. 2).\2\
Данные об оценки шпал сведены в таблицу 1.8
Таблица 1.8 Данные об отказах шпал
|
Наработка t, млн. т брутто |
Частота R(ti), шт/км |
Частность F(ti) |
Квантиль UРi |
|
360 |
14,01 |
0,007343 |
2.46 |
|
445 |
16,17 |
0,008475 |
2.41 |
|
530 |
49,49 |
0,025938 |
1.88 |
|
615 |
65,77 |
0,034471 |
1.82 |
|
700 |
87,02 |
0,045608 |
1.70 |
|
785 |
120,67 |
0,063244 |
1.51 |
Оценка параметров нормального распределения долговечности деревянных шпал Tcp и st определялась методом квантилей в сочетании с методом наименьших квадратов.
Далее с использованием полученных значений составляем систему уравнений:
Tcp – 2,46 st = 360 млн.т брутто;
Tcp – 2,41 st = 445 млн.т брутто;
Tcp – 1,88 st = 530 млн.т брутто;
Tcp – 1,82 st = 615 млн.т брутто;
Tcp – 1,70 st = 700 млн.т брутто;
Tcp – 1.51 st = 785 млн.т брутто;
Складывая левые и правые части уравнений получим:
6 Tcp – 11,78 st = 3435 млн.т брутто.
Умножая левые и правые части уравнений на квантили UPi
2,46 Tcp – 6,05 st = 886 млн.т брутто;
2,41 Tcp – 5,81 st = 1073 млн.т брутто;
1,88 Tcp – 3,53 st = 997 млн.т брутто;
1,82 Tcp – 3,31 st = 1120 млн.т брутто;
1.70 Tcp – 2,89 st =1190 млн.т брутто;
1,51 Tcp – 2,28 st = 1186 млн.т брутто;
Складывая левые и правые части уравнений системы получим:
11,78 Tcp – 23,87 st = 6452 млн.т брутто.
Значения параметров Tcp и st определим, решая систему полученных двух уравнений. Для рассматриваемого случая Tcp = 1345 млн. т, st = 394 млн. т.
Оценки доверительных границ (95%) для параметров Tcp и st производится по формулам (1.27) и (1.28).
Находим коэффициент усечения:
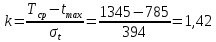
По приложению 3 /1/ для данного значения k находим :
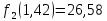 ;
;
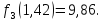
Тогда :
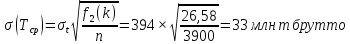
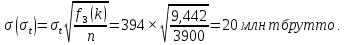
Находим 95% доверительный интервал:
Tcp(max/min) = 1348 ± 66 = 1282...1414 млн. т;
st(max/min) = 394 ± 40 = 354..434 млн. т.
Последовательность вычислений следующая. Определяем квантиль нормального распределения, соответствующий вероятности F(ti).
Зная квантиль U, определяем вероятность с использованием табулированной функции. Прогнозирование отказов шпал производится по формуле:
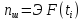
где Э – средняя эпюра шпал, по заданию 1908.
В связи с тем что используемая усеченная выработка и требуется высокая точность расчетов, интегральную функцию вероятности отказов определим по формуле.
Расчет сводится в таблицу 1.9
Таблица 1.9 Расчет отказов шпал
|
Наработка |
Вероятность Fшт |
Число отказов n, шт/км |
Приращение отказов, шт. |
|
360 |
0,0073 |
13,93 |
- |
|
445 |
0,0084 |
16,03 |
2,10 |
|
530 |
0,0259 |
49,42 |
33,39 |
|
615 |
0,0344 |
65,64 |
16,22 |
|
700 |
0,0456 |
87,00 |
21,37 |
|
785 |
0,0632 |
120,59 |
33,58 |
Наибольшую угрозу для безопасности движения поездов представляет образование кустов из трех и более негодных шпал. В соответствии с исследованиями вероятность такой ситуации определяется по зависимости
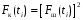 .
(1.48)
.
(1.48)
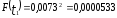
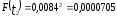
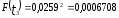
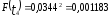
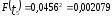
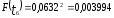
Количество кустов негодных шпал определится по формуле (1.47):
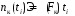 .
(1.49)
.
(1.49)
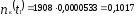 шт.;
шт.;
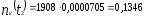 шт.;
шт.;
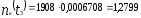 шт.;
шт.;
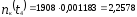 шт.;
шт.;
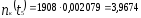 шт.;
шт.;
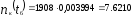 шт.;
шт.;
Образование кустов из трех и более шпал при наработке до 650 млн. т брутто маловероятно.
На рисунке 3 представлена зависимость суммарного выхода шпал от наработанного тоннажа

Рисунок 3. Зависимость суммарного выхода шпал от наработанного тоннажа:
1 – эмпирическая зависимость; 2 – теоретическая зависимость

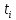 ,
млн. т
,
млн. т