2. Прогнозирование отказов рельсов

Совершенствование планирования ремонтов пути, управления запасами рельсов для одиночной смены и планирования проверок состояния рельсов средствами дефектоскопии диктует необходимость разработки методов прогнозирования отказов рельсов на основе апостериорной информации. Использование ПЭВМ в практике эксплуатации пути обусловливает повышенный интерес специалистов к организации эксплуатации рельсов по состоянию, так как ПЭВМ позволяет обработать в короткие сроки большие массивы информации об отказах рельсов и вычислить прогнозы возможного состояния их в будущем.

Рассмотрим методику прогнозирования отказов с использованием модели нормального распределения долговечности. Данное распределение полностью определяется заданием двух параметров – T_cp и s_t. При прогнозировании необходимо решить задачу: по известным оценкам T_cp и s_t вычислить точечный прогноз вероятности отказов рельсов F(t_i) при наработке t_i.

Последовательность вычислений следующая.

Определяем квантиль нормального распределения, соответствующий вероятности F(t_i), по формуле:

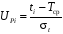. (1.32)

Зная квантиль U_Pi, определяем вероятность F(t_i) с использованием табулированной функции F₀(x), приведенной в приложении 1. Оценку суммарного выхода рельсов из расчета на один километр пути определим по формуле:

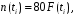(1.33)

где 80 – количество рельсов длиной 25 м на одном километре пути.

Для оценки точности выполним прогноз отказов рельсов с использованием упомянутых моделей на примере выборки из таблицы 1.1. Разделим выборку на обучающие и контрольные последовательности следующим образом. Если обучающая последовательность составлена при наработках 456 и 619 млн. т брутто (см. табл. 1.1), то контрольная – при 781 и 941 млн. т брутто, а если обучающая последовательность составлена при наработках 456, 619 и 781 млн. т брутто, то контрольная – при 941 , 1092 и 1254 млн. т брутто и т. д.

Обучающая последовательность, очевидно, должна включать два и более ретроспективных значения. Контрольная последовательность для расчетов точности прогноза принята равной двум, так как прогнозирование на три года и более вперед в условиях высокогрузонапряженных участков нецелесообразно.

Последовательность расчетов следующая.

На основании выборки, например, при 619 и 781 млн. т брутто выполняется оценка параметров T_cp и s_t. Далее с использованием зависимостей (1.32) и (1.33) вычисляется прогноз n(t) при наработках 941 и 1092 млн. т брутто. Относительная ошибка прогноза определяется по формуле:

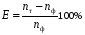, (1.34)

где n_т и n_ф – прогнозируемое и фактическое значения выхода рельсов, шт/км.

Результаты расчетов относительной ошибки прогноза для каждой модели представлены в таблице 1.2.

Таблица 1.2 Оценка точности прогнозирования

Наработка, млн. т брутто	Относительная ошибка, %, в зависимости от глубины прогноза
	1 год	2 года
619	18.61	64.64
781	33.96	16.91
941	9.02	14.78
1092	9.44	22.27
1254	16.62	36.3
Среднее Е	17.53	30.98

Из таблицы 1.2 видно, что при нормальном распределении среднее значение Е на 1-й год прогноза равно 17.53%, на 2-й год – 30.98%.

В ряде случаев бывает необходимо решить задачу, обратную приведенным примерам, а именно: по заданной вероятности отказа определить значения соответствующей ей наработки. Пусть задано F(t) = F(t_p). Этой функции соответствует нормированная функция F₀(x) = F₀(U_p), при этом t = t_p и x = U_p. Применительно к данному случаю квантиль U_p соответствует наработке, при которой будет иметь место заданная вероятность отказа. Значения функции F₀(U_p) и соответствующие ей значения U_p можно найти в специальных таблицах (прил. 2).

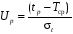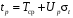и . (1.35)

Пример 1. Прогноз отказов рельсов можно использовать для планирования периодичности дефектоскопирования рельсов. В настоящее время при расчете этой периодичности за основу берется скорость развития поперечных усталостных трещин и достижения ими критических размеров около 30% площади головки рельса. При этом периодичность дефектоскопирования составляет от одного до трех раз в месяц в зависимости от величины наработанного тоннажа.

Рассмотрим отказы рельсов одного типа (Р65) одинакового качества (термоупрочненные) на участке длиной 48,75 км (3900 рельсов). Суммарный выход рельсов в соответствии с зависимостью (1.33) составит:

.

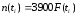В связи с тем, что используется усеченная выработка и требуется высокая точность расчетов, интегральную функцию вероятности отказов определим по формуле:

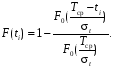(1.36)

Таблица 1.3 Расчет выхода рельсов

Наработка tp, млн. т	Квантиль	Вероятность F(ti)	Число отказов n(ti), шт/10 км	Приращение отказов, шт.
100	2.63	0,001201	0,9608	-
200	2.53	0,002639	2,1112	1,1504
300	2.42	0,004702	3,7616	1,6504
400	2.32	0,00712	5,696	1,9344
500	2.21	0,01051	8,408	2,712
600	2.10	0,014833	11,8664	3,4584
700	2.00	0,019738	15,7904	3,924
800	1.90	0,025727	20,5816	4,7912
900	1.79	0,033762	27,0096	6,428
1000	1.69	0,042569	34,0552	7,0456

Рисунок 1 График зависимости приращение отказов от наработки t_p

Пример 2. Рельсы Р65 термоупрочненные эксплуатировались на участке с осевыми нагрузками подвижного состава P_cp = 160 кН и средневзвешенным радиусом кривых R_cp = 1000 м. По результатам статистической обработки данных о выходе рельсов получены параметры нормального распределения их наработки: T_cp1 = 2606 млн. т и _t1 = 952 млн. т. После пропуска нормативного тоннажа (200 млн. т) рельсы отремонтированы с репрофилированием головки и переложены на участок с P_cp = 105 кН и R_cp = 1200 м.

Требуется определить предстоящий срок их службы в новых условиях до отказа 8 рельсов на километр.

Для решения этой задачи нужно определить параметры нормального распределения наработки по формуле:

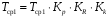, (1.37)

где –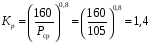

коэффициент, учитывающий влияние осевых нагрузок на срок службы рельсов;

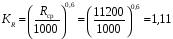
- коэффициент, учитывающий влияние кривизны пути на срок службы рельсов;

K_k = 0,8 – коэффициент, учитывающий качество отремонтированных рельсов.

В рассматриваемом случае

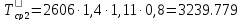млн. т;

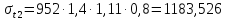млн. т.

Квантиль нормального распределения, соответствующий вероятности отказа 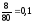, U_0,1 = 1,282.

Предстоящая наработка рельсов в новых условиях

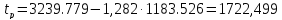млн. т.

Таким образом, в заданных условиях эксплуатации, отремон-тированные рельсы в новом пути могут прослужить до отказа 6 рельсов на километр до наработки в 1723 млн.т.