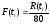2. Оценка и прогнозирование надежности рельсов

Для оценки надежности рельсов необходимы сведения об их отказах с момента укладки в путь. Такие данные можно взять из ведомостей учета рельсов, снятых с главных путей по изломам, порокам и повреждениям (ПУ-4) и рельсо-шпало-балластных карт.

Данные об отказах рельсов, включаемых в одну совокупность, должны соответствовать по следующим признакам:

• по типу рельсов (с учетом термообработки);

• роду шпал;

• роду балласта;

• типу плана;

• профиля пути;

• грузонапряженности;

• осевым нагрузкам;

• скоростям движения поездов и др.

Длина анализируемого участка пути определяется необходимой точностью получения показателей надежности рельсов. При планировании статистического эксперимента необходимо предусматривать объем выборки не менее 800 рельсов, т. е. длина анализируемого участка с однотипным верхним строением пути должна быть не менее 10 км. Из многочисленных наблюдений известно, что с ростом пропущенного тоннажа интенсивность отказов рельсов увеличивается.

В связи с этим будем использовать закон нормального распределения отказов.

1. Определение параметров нормального распределения

Закон нормального распределения полностью определяется двумя параметрами: T_cp (средняя наработка до 1-го отказа) и s_t (величина среднего квадратического отклонения).

Данные об отказах рельсов на некотором участке пути представляют собой вариационный ряд случайных чисел наработки до отказа (таблице 1.1).

Таблица 1.1 Параметры отказов рельсов

Наработка ti,млн.т	Частота R(ti), шт/км	Частость	Квантиль UPi
456	1,09	0,013625	2.19
619	1,55	0,019375	2.054
781	2,15	0,026875	1.92
941	2,67	0,033375	1.82
1092	4,17	0,052125	1.62
1254	6,17	0,077125	1.42

Пример вычислений первой строки таблицы 1.1:

• t_i и R(t_i) – по заданию с учетом номера варианта.

Частность 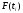– по формуле: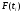

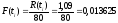
• Квантили U_Pi определяются по значениям частости F(t_i) с использованием приложения 2 методических указаний. Для этого вычисляем значение 1-F(t_i), затем находим заданное значение в 1 столбце приложения и в среднем столбце смотрим соответствующее ему значение квантиля (если нет точного соответствия то значение квантиля ищем способом интерполяции).

Запишем для каждой наработки t_i уравнения (1.24):

T_cp – 2,19 s_t = 456 млн.т брутто;

T_cp – 2,054 s_t = 619 млн.т брутто;

T_cp – 1,92 s_t = 781 млн.т брутто;

T_cp – 1,82 s_t = 941 млн.т брутто;

T_cp – 1,62 s_t = 1092 млн.т брутто;

T_cp – 1,42 s_t = 1254 млн.т брутто;

Складывая левые и правые части уравнений, получим:

6 T_cp – 11,024 s_t = 5143 млн.т брутто.

T_cp – 1,837 s_t = 857,167 млн.т брутто.

T_cp – 2,19 s_t = 456 млн.т брутто

0,353 s_t = 401,167 млн.т брутто

Значения параметров T_cp и s_t определим, решая систему полученных двух уравнений. Для рассматриваемого случая T_cp = 2606 млн. т, s_t = 952 млн. т.

Оценка доверительных границ (95%) найденных значений параметров T_cp и s_t производится по формулам:

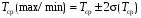; (1.27)

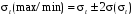. (1.28)

В зависимостях (1.27) и (1.28) значения s(T_cp) и s(s_t) вычисляются по следующим формулам:

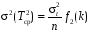; (1.29)

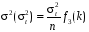, (1.30)

где k – коэффициент усечения выборки,

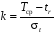, (1.31)

f₂(k) и f₃(k) – вспомогательные функции, определяемые по приложению 3 методических указаний;

n – количество обследуемых рельсов на данном участке.

Для вычисления доверительных интервалов для найденных параметров T_cp и s_t прежде всего находится коэффициент усечения:

k=( T_cp – t_r)/ s_t=(2606-1254)/952=1,50

По приложению 3 методических указаний для k = 1,50 находим f₂(1,50) =33,34 , f₃(1,50) =11,55 .

Тогда

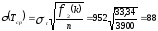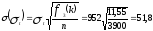млн.т брутто;

млн.т брутто.

Используя формулы (1.27) и (1.28), найдем 95%-ные доверительные интервалы:

T_cp(max/min) = 2606 ± 176 = 2430...2782 млн. т;

s_t(max/min) = 952 ± 103,6 = 848,4...1055,6 млн. т.

Таким образом, параметры нормального распределения для заданных параметров надежности железнодорожного пути определены и составляют: средняя наработка до первого отказа в пределах доверительного интервала – 2430...2782 млн. т, величина среднего квадратического отклонения – 848,4...1055,6 млн. т.