
- •Высшего профессионального образования
- •Высшая математика
- •Г. Набережные Челны
- •1.Цель и задачи дисциплины, её место в учебном процессе.
- •2. Содержание и структура дисциплины (семестр 2).
- •2.1. Содержание дисциплины (наименование и номера тем).
- •Раздел I. Дифференциальное исчисление функции одной переменной.
- •Тема 1. Производные и дифференциалы функции одной переменной.
- •Тема 2. Основные теоремы о дифференцируемых функциях и их приложения.
- •Тема 3. Исследование функций с помощью производных, построение их графиков.
- •Раздел II. Функции нескольких переменных.
- •Тема 4. Основные понятия о функции нескольких переменных.
- •Тема 5. Производные и дифференциалы функции нескольких переменных, их приложения.
- •Тема 6. Экстремумы функций нескольких переменных.
- •2.2. Практические занятия, их содержание.
- •Тема 1. Производные и дифференциалы функции одной переменной.
- •Тема 2. Основные теоремы о дифференцируемых функциях и их приложения. Исследование функций с помощью производных, построение их графиков.
- •Тема 3. Функция -переменных. Производные и дифференциалы функции нескольких переменных.
- •Тема 4. Производная по направлению и градиент. Экстремумы функций нескольких переменных.
- •2.3. Виды самостоятельной работы студентов.
- •3. Рекомендуемая литература: Основная литература:
- •Дополнительная литература:
- •4. Методические указания по изучению дисциплины.
- •5. Материалы для контроля знаний студентов.
- •5.1. Задания для контрольной работы (семестр 2).
- •Раздел I. Дифференциальное исчисление функции одной переменной.
- •Раздел II. Функции нескольких переменных.
- •5.2. Вопросы к экзамену (семестр 2).
- •Раздел I..Дифференциальное исчисление функции одной переменной.
- •Раздел II. Функции нескольких переменных.
- •6. Приложения.
- •6.1. Образец решения контрольных задач типового варианта. Семестр 2.
- •6.2. Краткие теоретические сведения.
- •Тема 1. Производные и дифференциалы функции одной переменной.
- •Тема 2. Основные теоремы о дифференцируемых функциях и их приложения.
- •Тема 3. Исследование функций с помощью производных, построение их графиков.
- •3.1 Возрастание, убывание функций. Экстремум.
- •3.2 Наибольшее и наименьшее значения функции.
- •3. 3 Выпуклость, вогнутость, точки перегиба. Асимптоты.
- •3.4 Построение графиков функций.
- •Тема 4. Основные понятия о функции нескольких переменных.
- •Тема 5. Производные и дифференциалы функции нескольких переменных, их приложения.
- •5.2 Элементы теории поля. Производная по направлению и градиент.
- •5.3 Неявные функции.
- •Тема 6. Экстремумы функций нескольких переменных.
- •6.3 Основные математические формулы. Формулы сокращённого умножения:
- •Формулы тригонометрии:
- •Формулы приведения.
- •Значения тригонометрических функций некоторых углов.
- •Элементарных функций.
- •6.4 Образец оформления обложки с контрольной работой. Федеральное агентство по образованию Государственное образовательное учреждение
- •«Камская государственная инженерно-экономическая академия»
- •Набережные Челны
Раздел II. Функции нескольких переменных.
6.
Для указанной
функции
![]() требуется: найти а)
полный
дифференциал
требуется: найти а)
полный
дифференциал
![]() ;
б)
смешанную производную
;
б)
смешанную производную
![]() .
.
6.1.
![]() ,
6.2.
,
6.2.
![]() ,
,
6.3.
![]() ,
6.4.
,
6.4.
![]() ,
,
6.5.
![]() ,
6.6.
,
6.6.![]() ,
6.7.
,
6.7.![]() ,
6.8.
,
6.8.
![]()
6.9.
![]() 6.10.
6.10.
![]()
-
 6.12.
6.12.
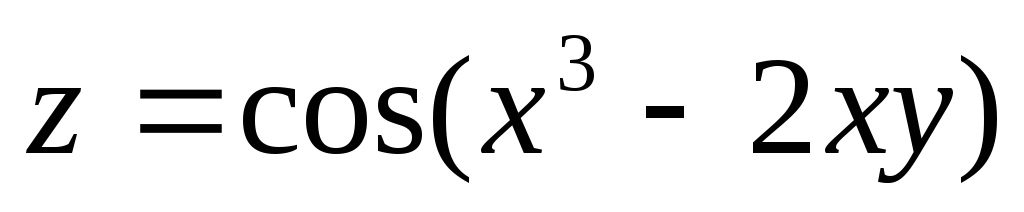
6.13.![]() 6.14.
6.14.![]()
-
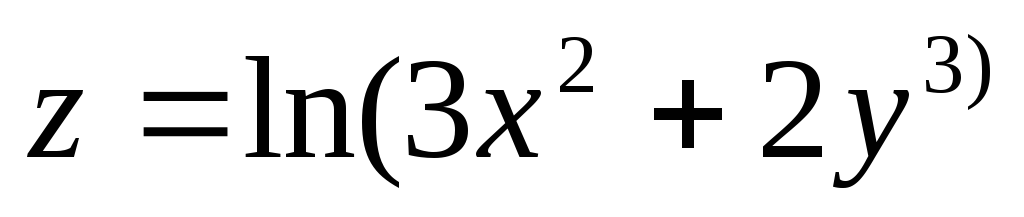 6.16.
6.16.
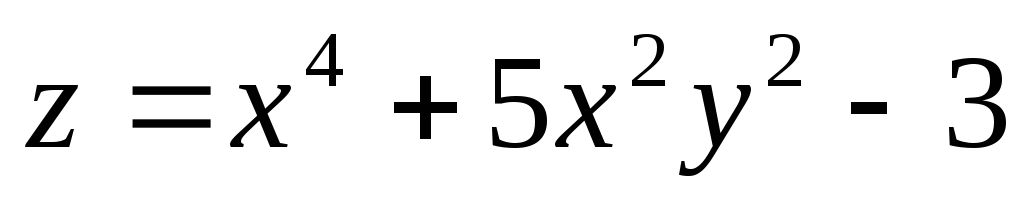
-
 6.18.
6.18.

-
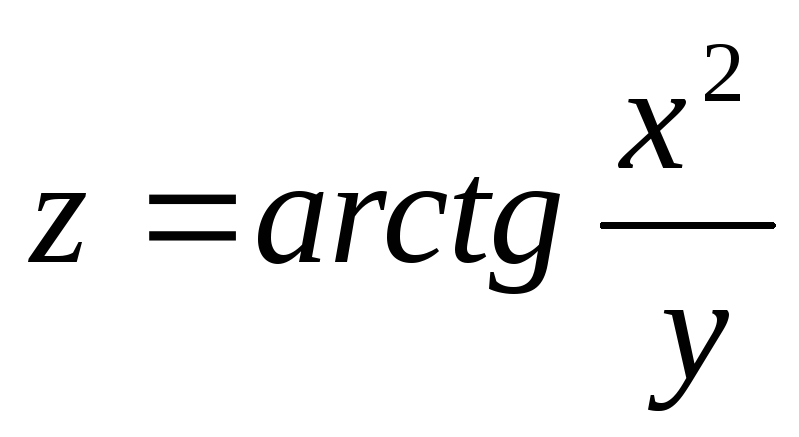 6.20.
6.20.

-
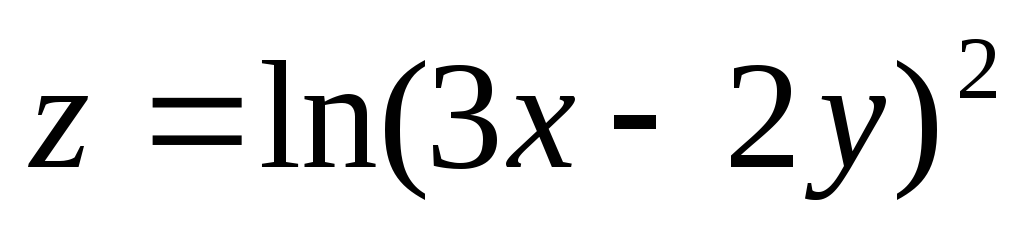 6.22.
6.22.
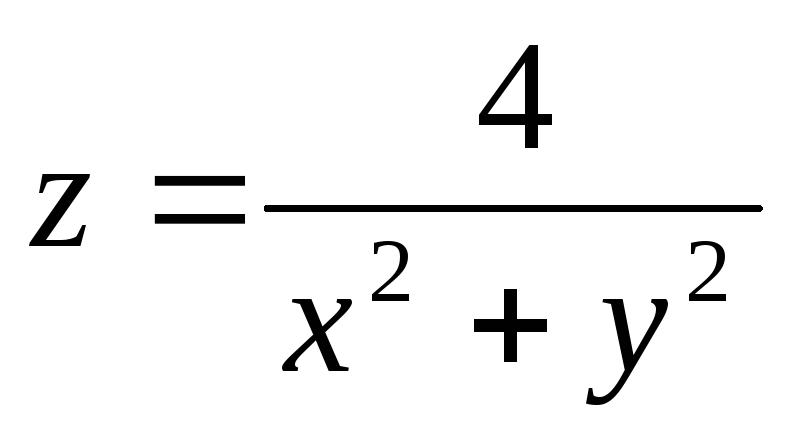
-
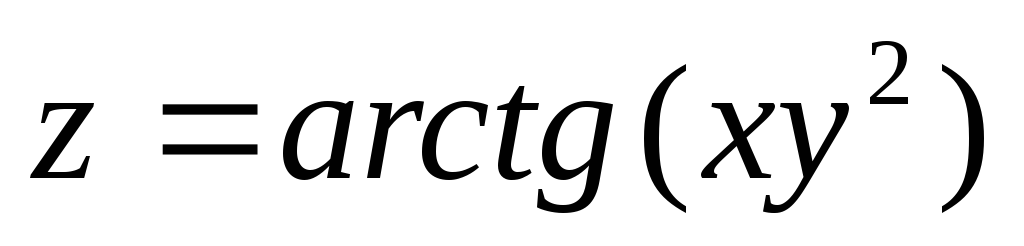 6.24.
6.24.
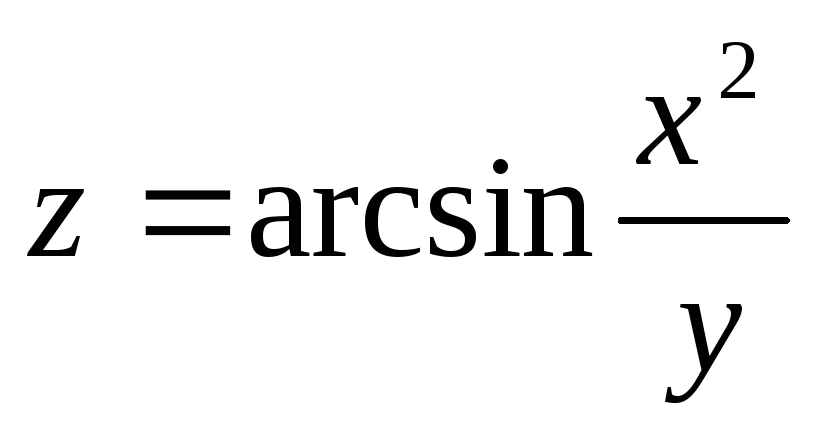
-
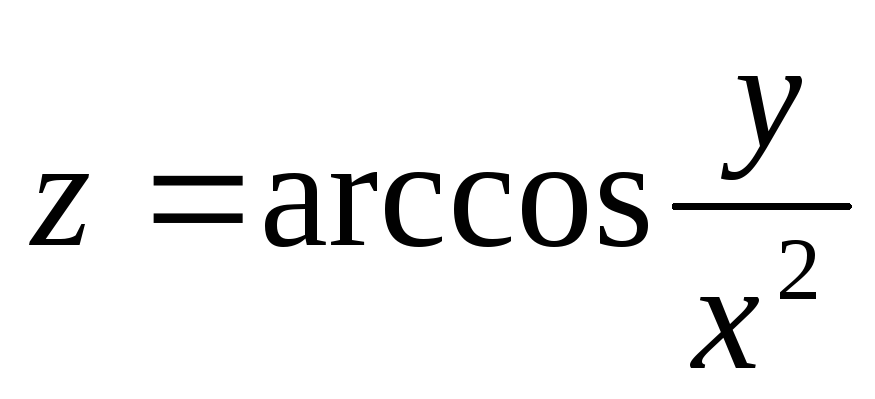 6.26.
6.26.
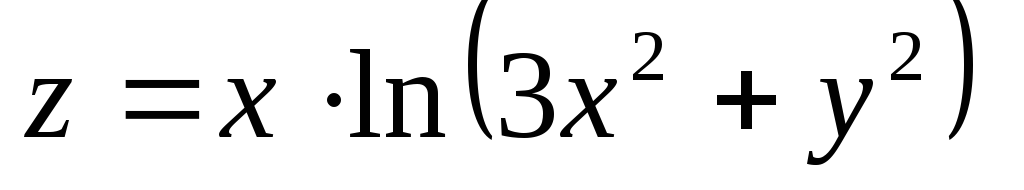
-
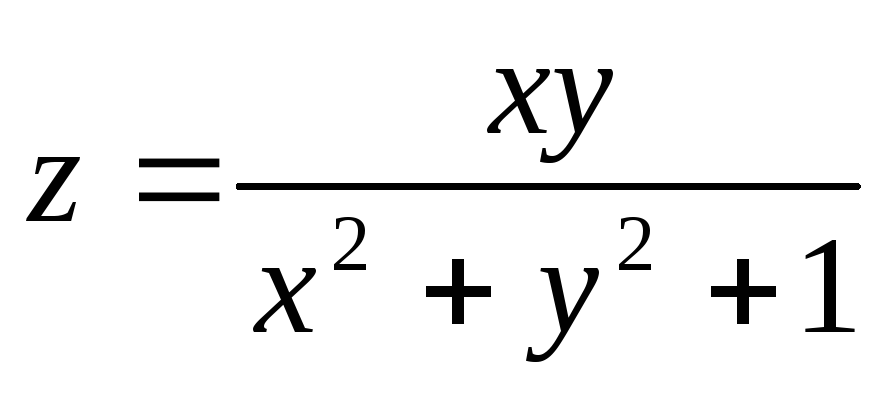 6.28.
6.28.
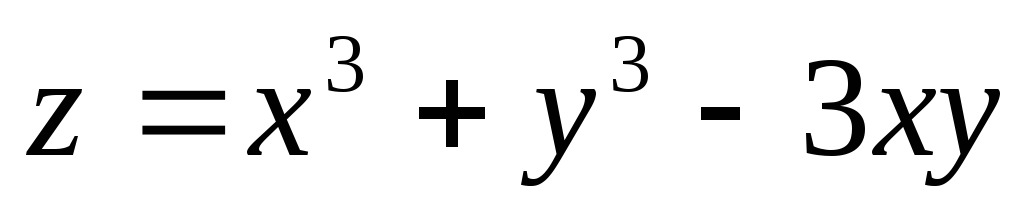
6.29.
![]() 6.30.
6.30.
![]()
7.
Для функции![]() ,
заданной неявно, найти частные производные
,
заданной неявно, найти частные производные
![]() и
и
![]() .
.
7.1![]() 7.2.
7.2.
![]()
7.3.
![]() 7.4.
7.4.
![]()
7.5.
![]() 7.6.
7.6.
![]()
7.7.
![]() 7.8.
7.8.
![]()
7.9.
![]() 7.10.
7.10.
![]() 7.11.
7.11.
![]() 7.12.
7.12.
![]() 7.13.
7.13.
![]() 7.14.
7.14.
![]() 7.15.
7.15.
![]() 7.16.
7.16.
![]() 7.17.
7.17.
![]() 7.18.
7.18.
![]() 7.19.
7.19.
![]() 7.20.
7.20.
![]() 7.21.
7.21.
![]() 7.22.
7.22.
![]() 7.23.
7.23.
![]()
7.24.
![]()
7.25.
![]()
7.26.
![]()
7.27.
![]() 7.28.
7.28.
![]() 7.29.
7.29.![]() 7.30.
7.30.
![]()
8.
Найти локальные экстремумы функции
![]()
8.1.
![]() 8.2.
8.2.![]() ,
,
![]()
8.3.
![]() 8.4.
8.4.
![]() ,
,
![]()
8.5.
![]() ,
,
![]() 8.6.
8.6.
![]()
8.7.
![]() 8.8.
8.8.
![]()
8.9.
![]() 8.10.
8.10.
![]()
8.11.![]() .
8.12.
.
8.12.![]()
8.13.
![]() 8.14.
8.14.
![]()
8.15.![]() 8.16.
8.16.![]()
-
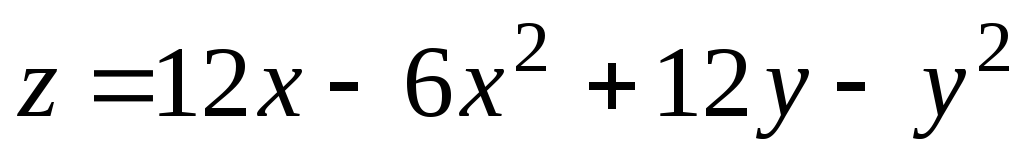 8.18.
8.18.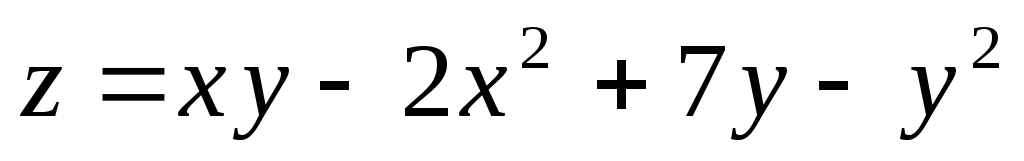
8.19.![]() 8.20.
8.20.
![]()
8.21.![]() 8.22.
8.22.![]()
-
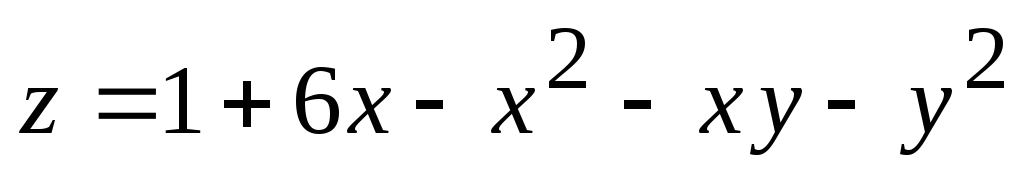 8.24.
8.24.

8.25.![]()
8.26.
![]() 8.27.
8.27.
![]()
8.28.![]() 8.29.
8.29.
![]()
8.30.![]()
9.
Найти условные
экстремумы функции
![]() (методом
Лагранжа):
(методом
Лагранжа):
9.1.
![]() при
при
![]()
9.2.
![]() при
при
![]()
9.3.
![]() при
при
![]()
9.4.
![]() при
при
![]()
9.5.
![]() при
при
![]()
9.6.
![]() при
при
![]()
9.7.
![]() при
при
![]()
9.8.
![]() при
при
![]()
9.9.
![]() при
при
![]()
9.10.
![]() при
при
![]()
9.11.
![]() при
при
![]()
9.12.
![]() при
при
![]()
9.13.
![]() при
при
![]()
9.14.
![]() при
при
![]()
9.15.
![]() при
при
![]()
9.16.
![]() при
при
![]()
9.17.
![]() при
при
![]()
9.18.
![]() при
при
![]()
9.19.![]() при
при
![]()
9.20.
![]() при
при
![]()
9.21.
![]() при
при
![]()
9.22.
![]() при
при
![]()
9.23.
![]() при
при
![]()
9.24.
![]() при
при
![]()
9.25.
![]() при
при
![]()
9.26.
![]() при
при
![]()
9.27.
![]() при
при
![]()
9.28.
![]() при
при
![]()
9.29.
![]() при
при
![]()
9.30.
![]() при
при
![]()
10.
Найти наибольшее и наименьшее значения
функции
![]() в ограниченной и замкнутой области D:
в ограниченной и замкнутой области D:
10.1.
![]() ,
,
![]() .
.
10.2.
![]() ,
,
![]() .
.
10.3.
![]() ,
,
![]() .
.
10.4.
![]() ,
,
![]() .
.
10.5.
![]()
![]() .
.
10.6.
![]() ,
,
![]() .
.
10.7.
![]() ,
,
![]() .
.
10.8.
![]() ,
,
![]() .
.
10.9.
![]() ,
,![]() .
.
10.10.
![]() ,
,
![]() .
.
10.11.
![]() ,
,
![]() .
.
10.12.
![]() ,
,
![]() .
.
10.13.
![]() ,
,
![]() .
.
10.14.
![]() ,
,
![]() .
.
10.15.
![]() ,
,
![]() .
.
10.16.
![]() ,
,
![]() .
.
10.17.
![]() ,
,
![]() .
.
10.18.
![]() ,
,
![]() .
.
10.19.
![]() ,
,
![]() .
.
10.20.
![]() ,
,
![]() .
.
10.21.
![]() ,
,
![]() .
.
10.22.
![]() ,
,
![]() .
.
10.23.
![]() ,
,
![]() .
.
10.24.
![]() ,
,
![]() .
.
10.25.
![]() ,
,
![]() .
.
10.26.
![]() ,
,
![]() .
.
10.27.
![]() ,
,
![]() .
.
10.28.
![]() ,
,
![]() .
.
10.29.
![]() ,
,
![]() .
.
10.30.
![]() ,
,
![]() .
.
11.
Найти: а) координаты градиента функции![]() в точке
в точке
![]() ;
б) уравнения касательной плоскости и
нормали к поверхности, заданной
уравнением
;
б) уравнения касательной плоскости и
нормали к поверхности, заданной
уравнением![]() в точке
в точке
![]() .
.
11.1
![]() ,
,
![]()
11.2.
![]() ,
,
![]()
11.3.
![]() ,
, ![]()
-
 ,
,
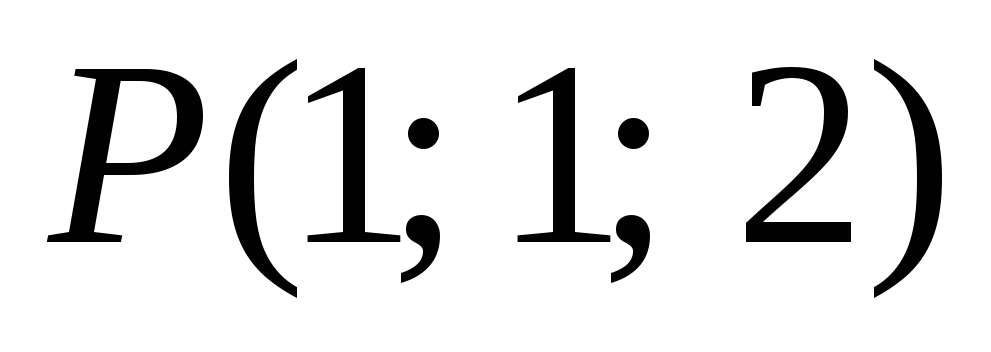
11.5.
![]() ,
,
![]()
11.6..![]() ,
,
![]()
11.7..
![]() ,
,
![]()
11.8.
![]() ,
,
![]()
-
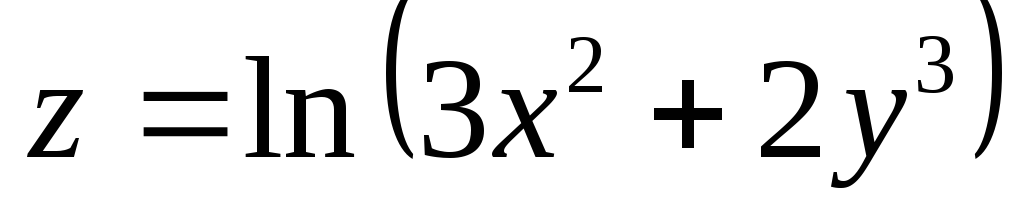 ,
,
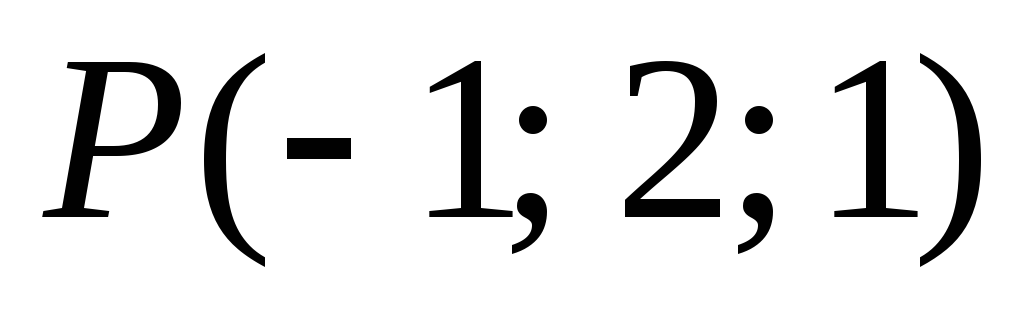
-
 ,
,
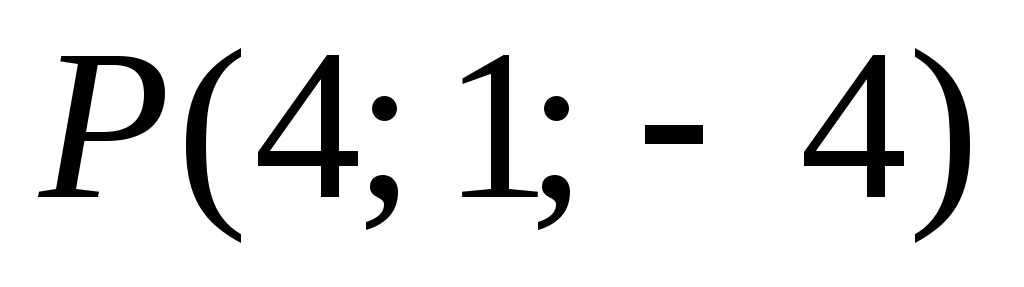
-
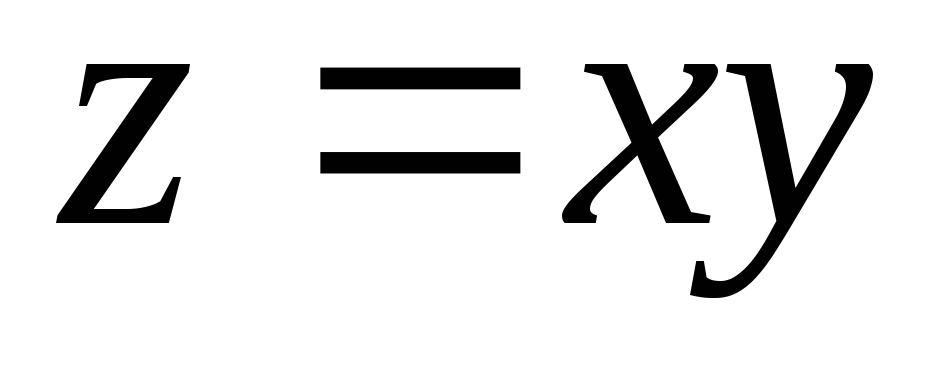 ,
,

-
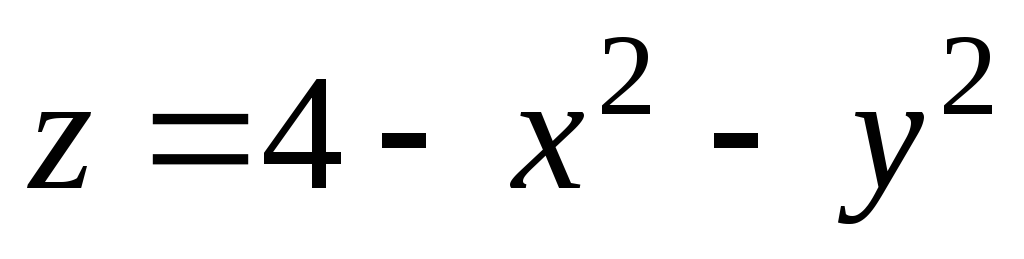 ,
,
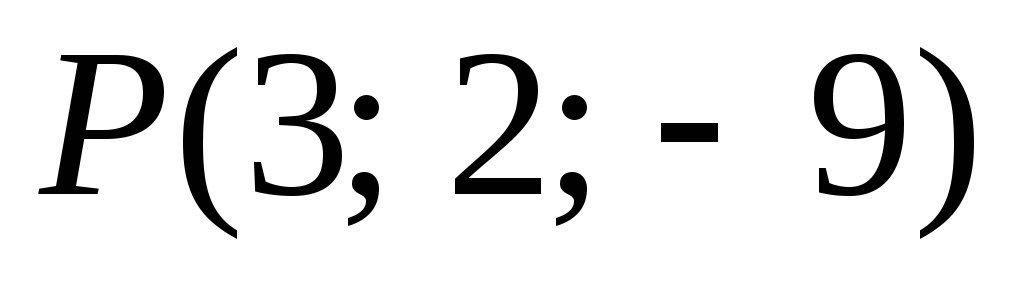
-
 ,
,
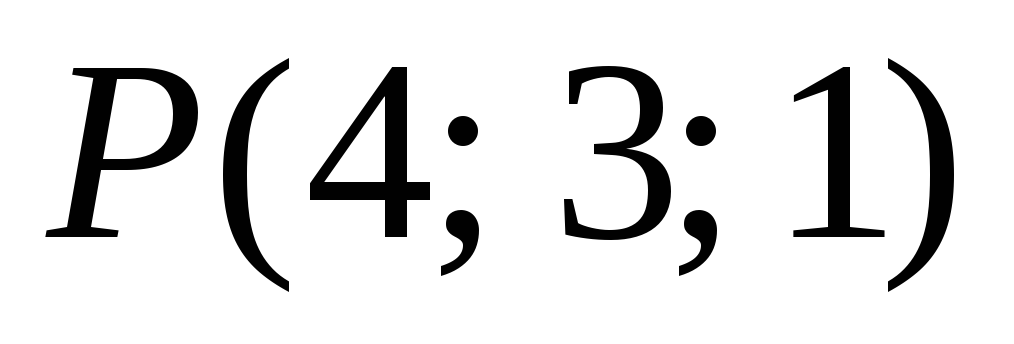
-
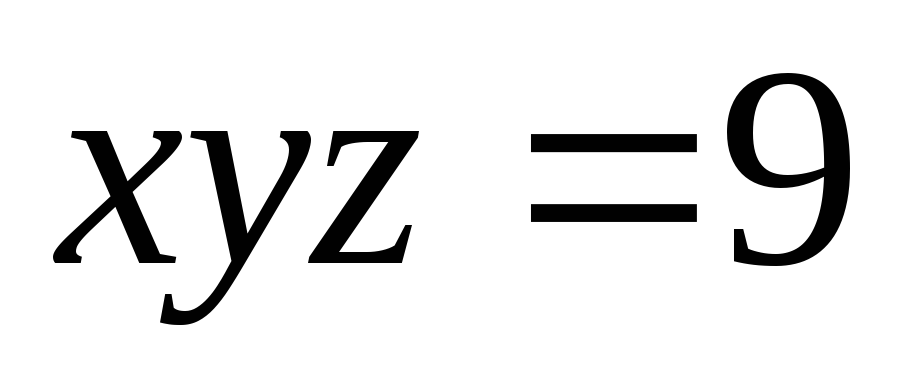 ,
, 
-
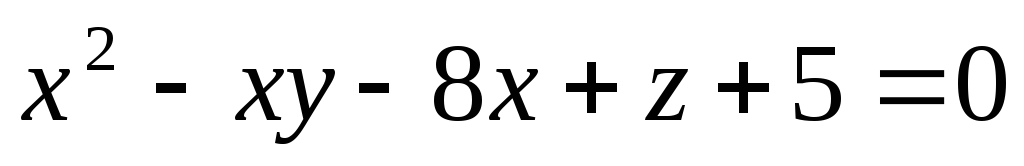 ,
,

-
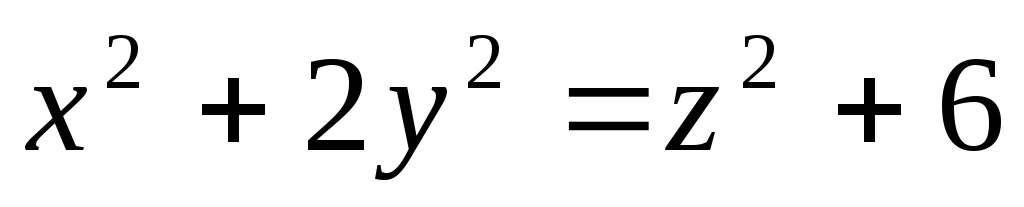 ,
,
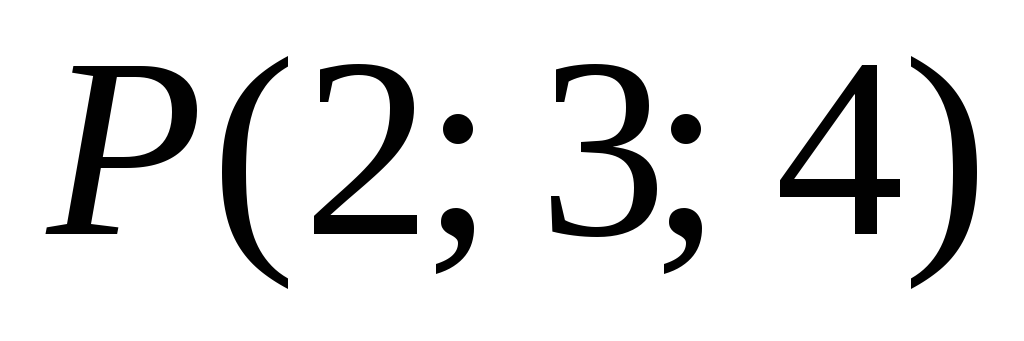
-
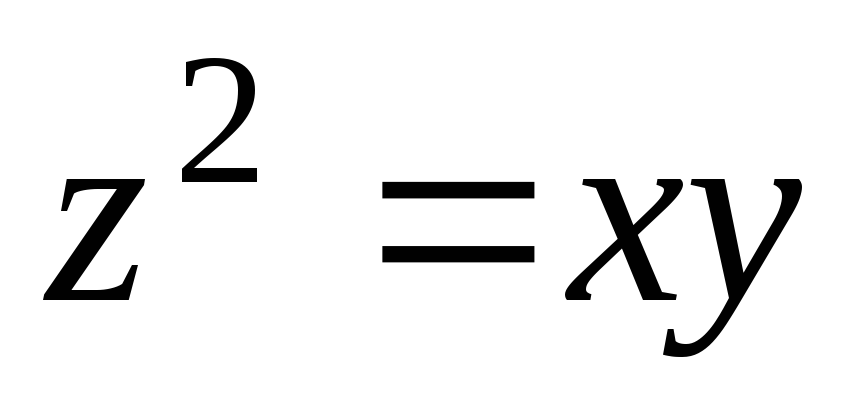 ,
,
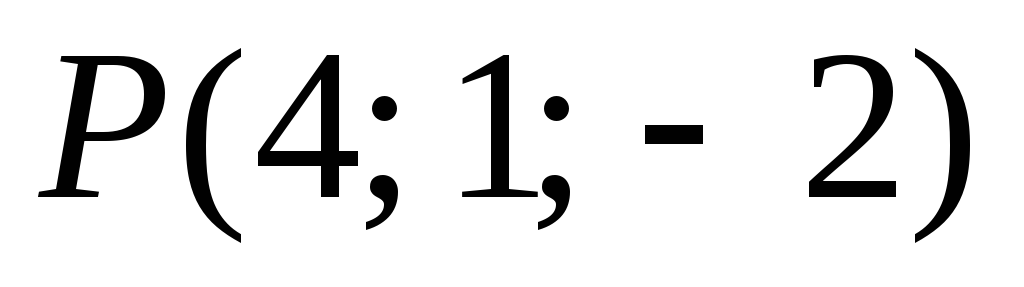
-
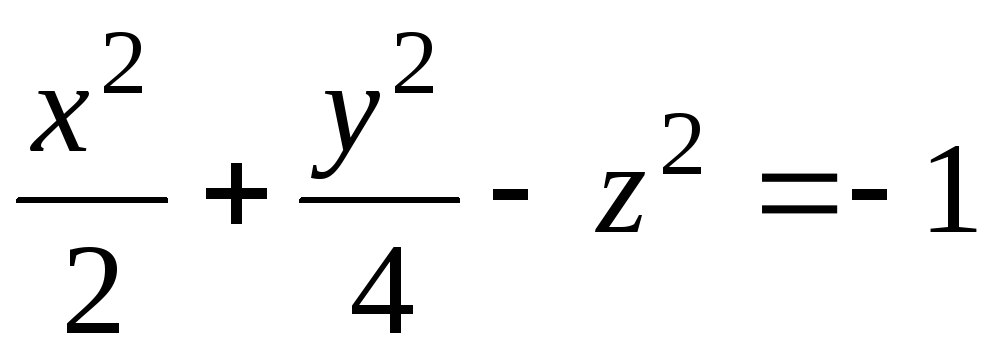 ,
,
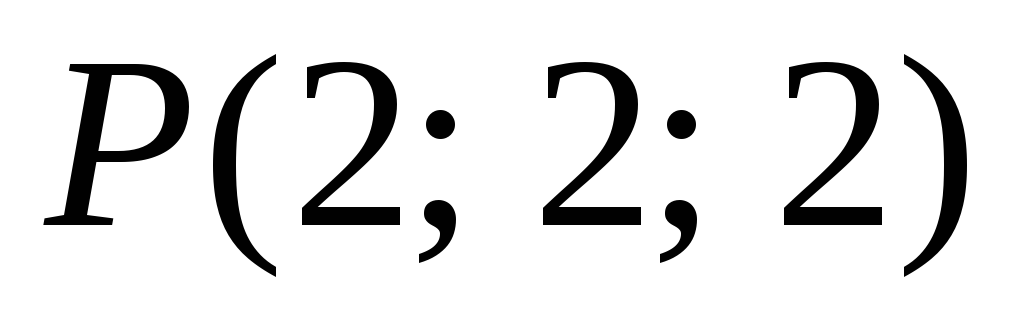
-
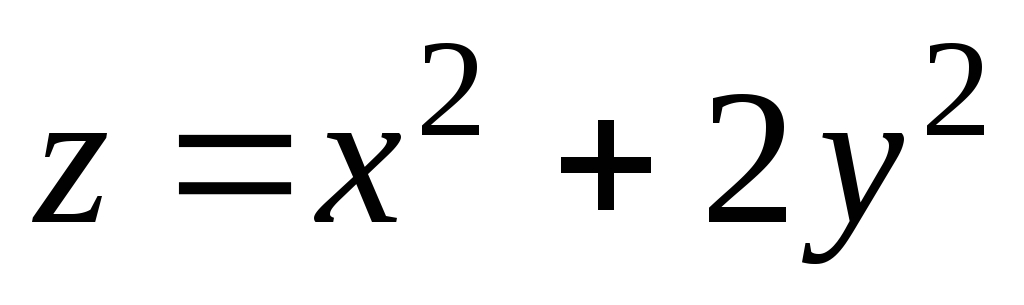 ,
,
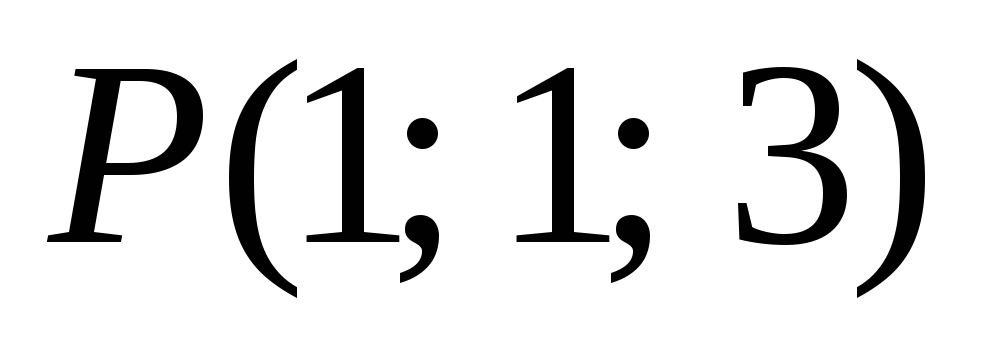
-
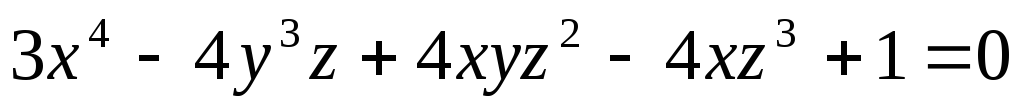 ,
,
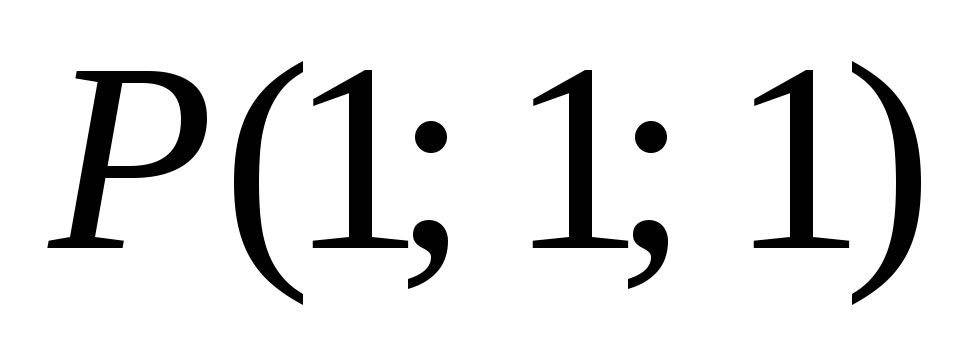
-
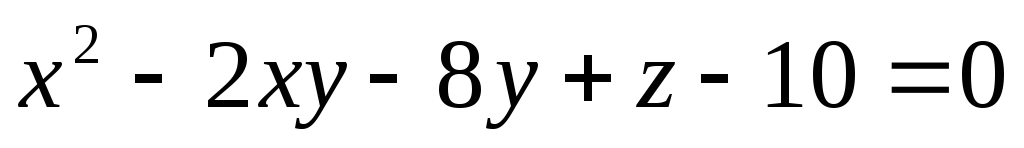 ,
,
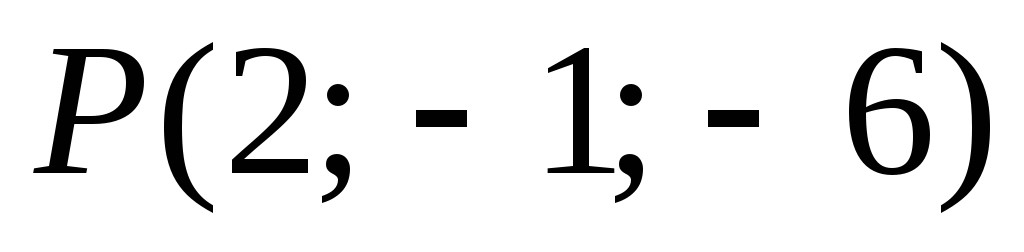
-
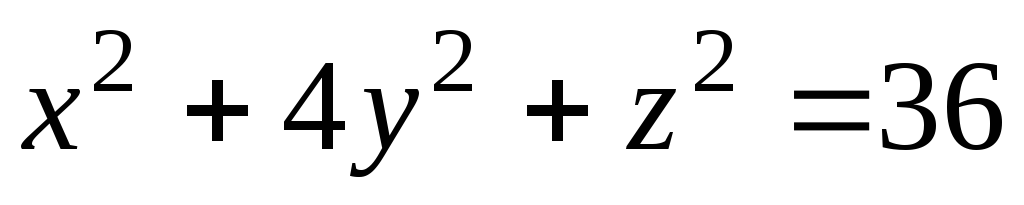 ,
,
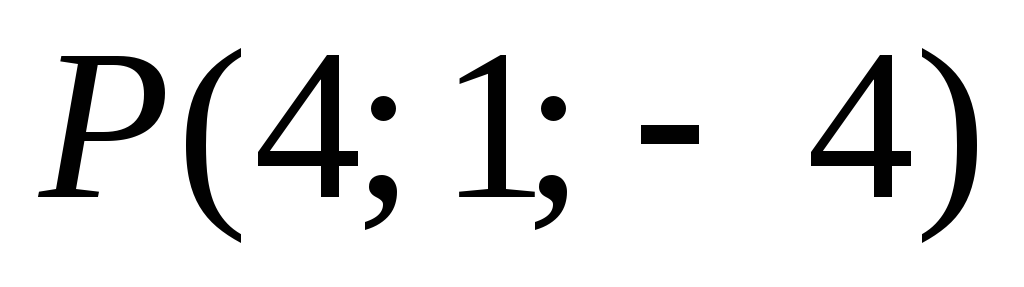
-
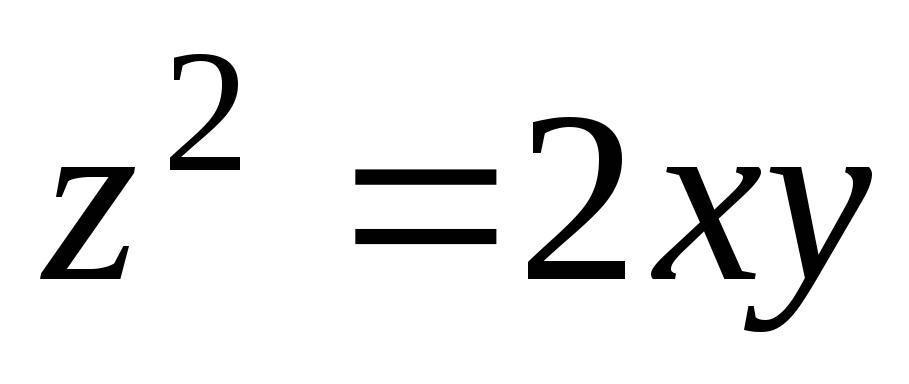 ,
,
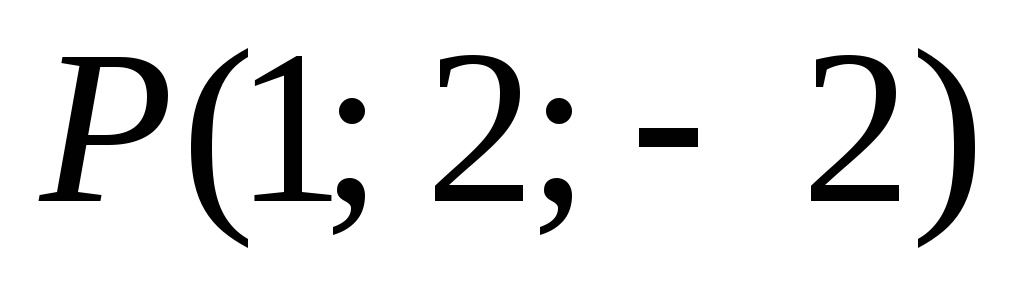
-
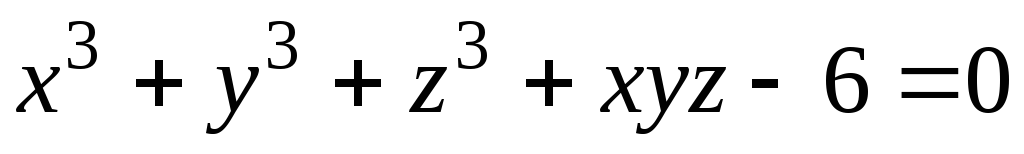 ,
,
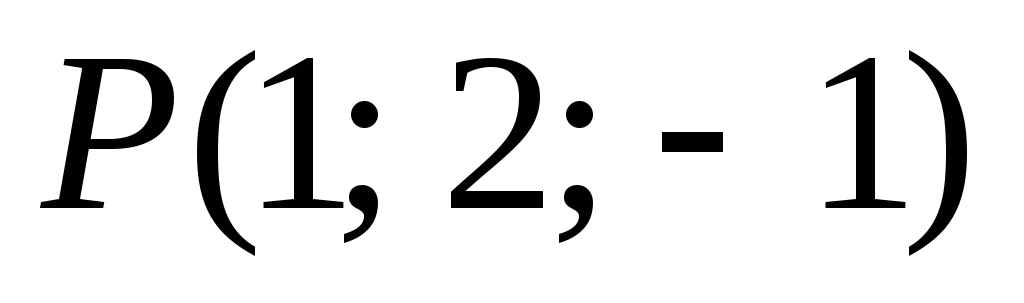
-
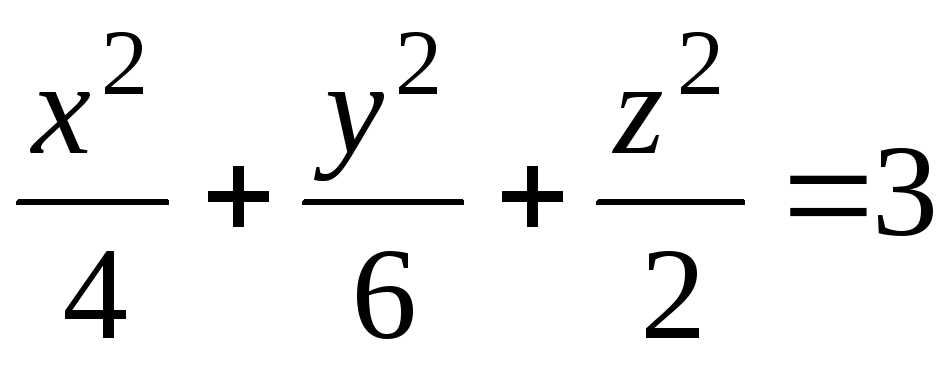 ,
,
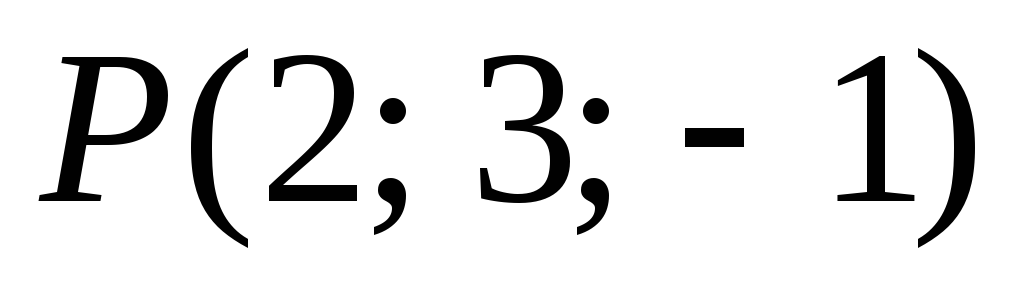
-
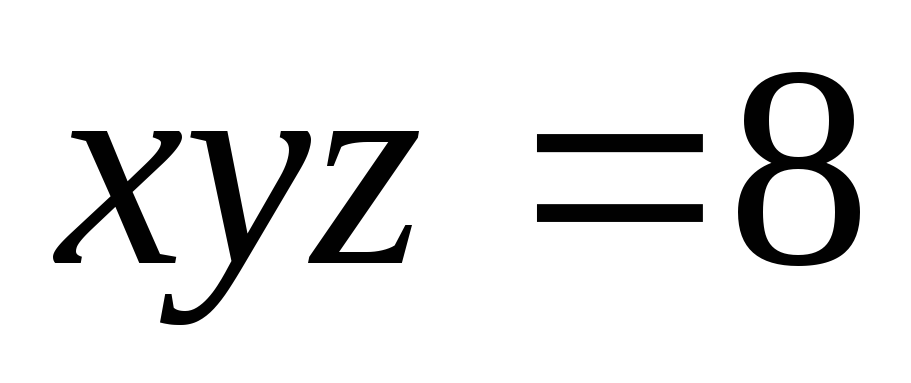 ,
,
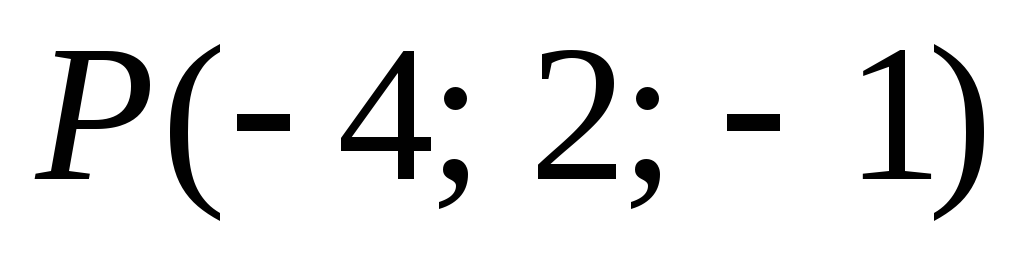
-
 ,
, 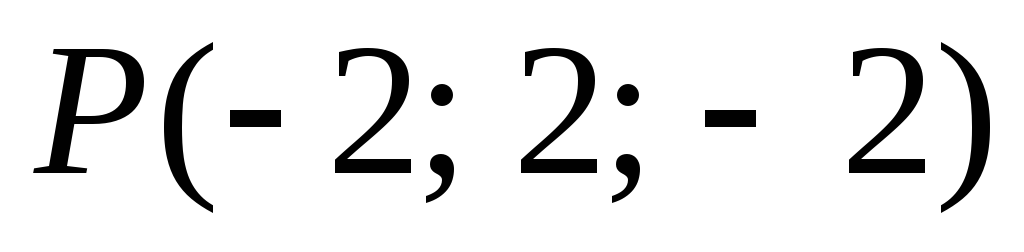
-
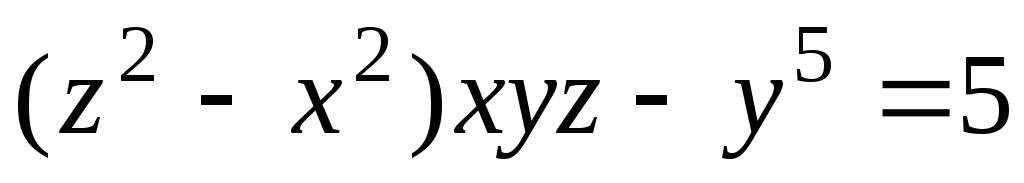 ,
,
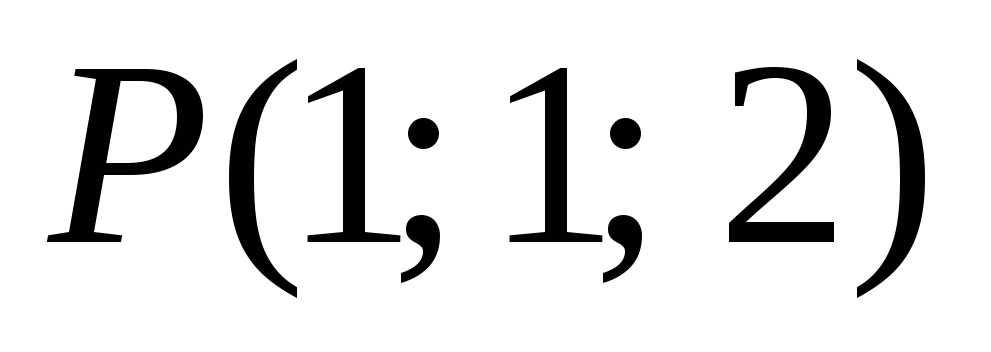
-
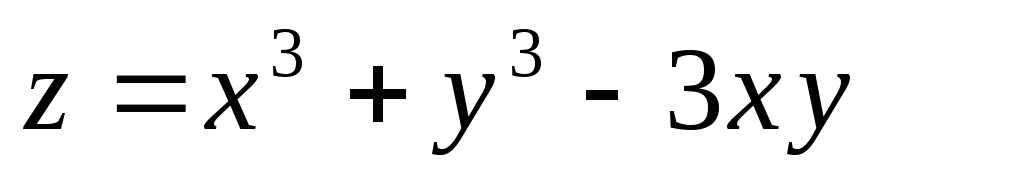 ,
,
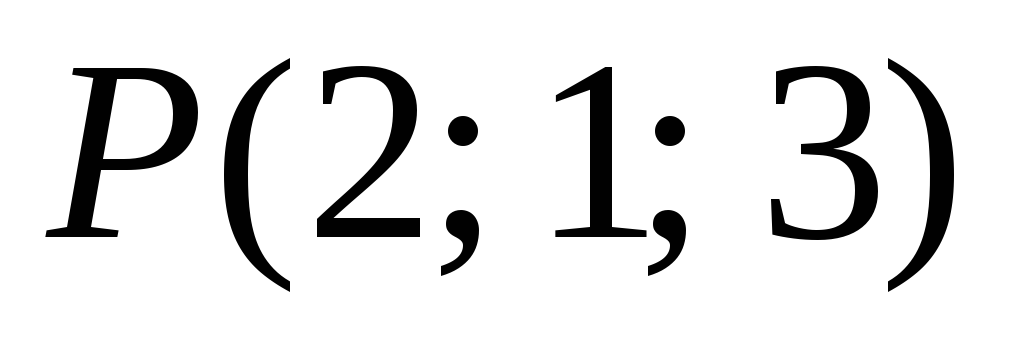
11.30.
.![]() ,
,
![]()
