5.2 Элементы теории поля. Производная по направлению и градиент.

Пусть - область в двумерном пространстве. Скалярным полем на называется числовая функция , заданная в точках . Линии , где называются линиями уровня скалярного поля .

Пусть - область в трёхмерном пространстве.

Скалярным полем на называется числовая функция , заданная в точках . Поверхности , где называются поверхностями уровня скалярного поля .

Градиентом скалярного поля называется вектор

.

Производная скалярного поля по направлению произвольного вектора вычисляется по формуле , где , , - направляющие косинусы вектора .

Градиент скалярного поля в точке направлен по нормали к поверхности уровня , проходящей через в сторону возрастания поля, а его модуль равен наибольшей производной по направлению в этой точке.

5.3 Неявные функции.

Если уравнение , где - дифференцируемая функция по переменным , определяет как функцию независимых переменных , то частные производные этой неявной функции вычисляются по формулам: ,,…, при условии, что .

В частности, для функции , заданной неявно уравнением справедлива формула , при условии , а для функции , заданной уравнением

справедливы формулы:,, при условии.

Частные производные высших порядков вычисляются последовательным дифференцированием данных формул.

Уравнение касательной плоскости к поверхности , заданной неявным уравнением , в точкеимеет вид , а уравнение нормали –вид .

Тема 6. Экстремумы функций нескольких переменных.

Точка , принадлежащая области определения функции , называется стационарной точкой функции, если в этой точке каждая из её частных производных равна нулю, т.е. ,…, или .

Точка называется точкой минимума (максимума) функции , если существует окрестность точки такая, что для всех точек этой окрестности выполняется неравенство ().

Точки минимума и максимума функции называются точками экстремума, а значения функции в этих точках – экстремумами функции.

Необходимое условие экстремума. Если - точка локального экстремума функции , дифференцируемой в точке, то - стационарная точка функции.

Достаточное условие экстремума. Пусть - стационарная точка дважды дифференцируемой в точке функции _. Тогда, если при всевозможных наборах значений , не равных одновременно нулю:

1) , то в точке функция имеет максимум; 2) , то в точке функция имеет минимум; 3) принимает как положительные, так и отрицательные значения, то в точке функция не имеет экстремума.

Исследование знака сводится к исследованию знакоопределённости второго дифференциала, как квадратичной формы относительно переменных(например, с помощью критерия Сильвестра).

В частности, функция в стационарной точке , при условии , где ,, : 1) имеет максимум, если и ; 2) имеет минимум, если и ; 3) не имеет экстремума, если .

Точка называется точкой условного минимума (максимума) функции , если существует окрестность точки такая, что для всех точек этой окрестности, удовлетворяющих уравнениям связи () выполняется неравенство (). Точки условного минимума и максимума функции называются точками условного экстремума, а значения функции в этих точках – условными экстремумами функции.

Задача нахождения условного экстремума сводится к нахождению обычного экстремума функции Лагранжа , где () –постоянные множители Лагранжа.

Необходимое условие условного экстремума. Если - точка условного экстремума функции при наличии уравнений связи () , то в точке выполняются условия

.

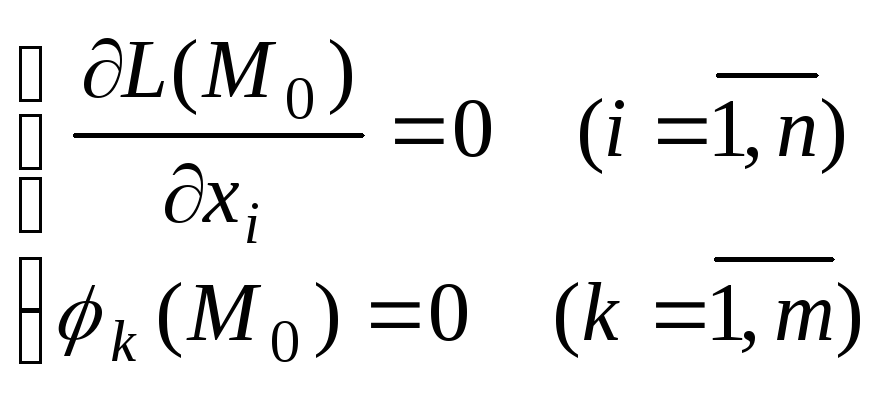Решая данную систему, находят неизвестные координаты точки , в которой возможен условный экстремум и соответствующие ей значения множителей Лагранжа .

Вопрос о существовании и характере условного экстремума решается на основании изучения (например, с помощью критерия Сильвестра) знака второго дифференциала функции Лагранжа в точке при значениях , рассматриваемого как квадратичная форма относительно переменных при условии, что они связаны соотношениями: ().

В частности, для функции исследуется знак при условии.

Достаточное условие условного экстремума. Пусть - точка возможного условного экстремума функции , т.е. в этой точке выполнены необходимые условия условного экстремума. Тогда, если при всевозможных наборах значений , удовлетворяющих соотношениям () и не равных одновременно нулю: 1) , то в точке функция имеет условный максимум; 2) , то в точке функция имеет условный минимум; 3) принимает как положительные, так и отрицательные значения, то в точке функция не имеет условного экстремума.

Если функция дифференцируема в ограниченной и замкнутой области, то она достигает своих наибольшего и наименьшего значений в этой области или в стационарной точке, или в граничной точке области.