11. Фрезерование фасонных поверхностей.

Ф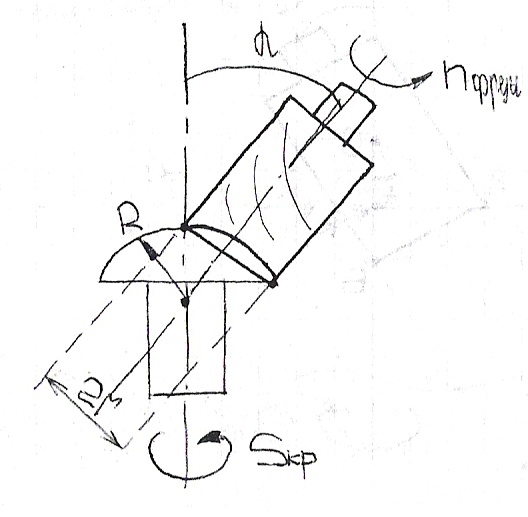 резерование- это процесс прерывистого резания, осуществляемый многолезвийным режущем инструментом (фрезой), который совершает главное вращательное движение со V резанья, а движение подачи S сообщается , как правило, заготовки, реже инструментом, закрепленном на столе фрезерного станка в спец. приспособлений ( угольники, плиты, УДГ)

По виду подачи и виду полируемой поверхности все способы фрезерования на 6 групп:

1)плоское периферийное фрезерование, плоское торцевое фрезерование и периферийно-торцевое.

-торцеовое фрезерование гориз. плоскости на горизонтальном фрезерном станке

цилиндрической фрезой с косым зубом;

2)Круглое фрезерование:

Осуществляется круговым движением подачи заготовки в результате чего образуются цилиндрические поверхности, как наружные, так и внутреннее.

3)Винтовое фрезерование: получение винтовых поверхностей (резьбо-фрезерование, фрезерование цилиндрических червяков, фрезерование винтовых канавок)

4) Профильное фрезерование (фасонный профиль детали получается копированием фасонного круга фрезы)

а) круговое профильное фрезерование

б) продольное профильное фрезерование (рис и))

5) Фасонное фрезерование (рис к)

Осуществляется при управлении движения подачи заготовки по 3м координатным осям (получение пл-ей объемных фасонных деталей)

Метод может быть реализован на гравировально- фрезерном станке или на станках с ЧПУ.

Осуществляется с помощью продольной фасонной фрезы (напр. Долбека, который с главным движением вращения совершит движения обкатки вокруг заготовки)

К наиболее распространенным фасонным поверхностям, получаемым методом фрезерования относятся поверхности, заданые не аналитическим методом:

а) непрерывный поверхности вращения с производной образующей.

б)Косые цилиндрические поверхности типа переменной малки, поверхности замкнутого контура.

В)линейчатые цилиндрические поверхности с производной направляющей, фасонные поверхности незамкнутого контура.

12. Фрезерование сферических поверхностей.

Сферическими называются поверхности, содержащими сферу или её часть. Часть сферы, отсеченная от нее плоскостью, называется сегментной шаровой поверхностью. Часть сферы, замкнутая м/у 2-я параллельными плоскостями называется шаровым поясом. В условиях единичного и мелкосерийного производства такие поверхности образуются на универсальных, вертикально- фрезерных станках с помощью концевых радиальных сфер или специальных резцовых головок. В качаестве примера таких поверхностей можно рассматривать приспособление : анка с пунзелами.

Фрезерование внутренней сферической поверхности.

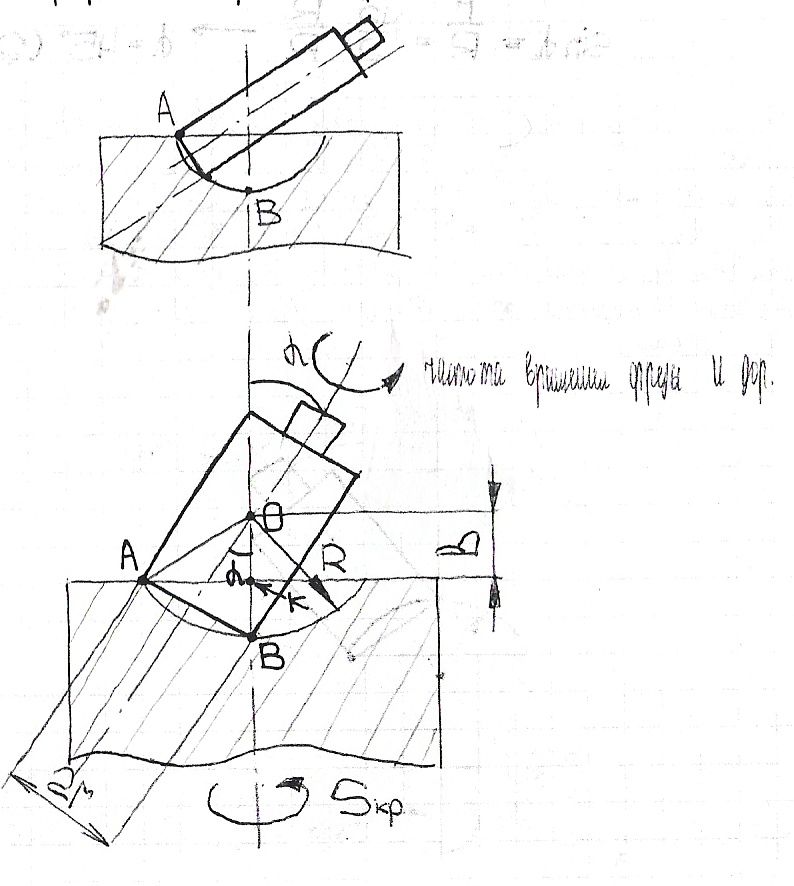
Для получения внутренней сферической поверхности ось вращения фрезы и ось вращения заготовки должны располагаться под неким углом α по отношению друг к другу.

Рассмотрим ΔАОК и ΔАВК

ΔАОК:→найдем катет АК; АК²=R²-ОК²

ΔАВК:→АК²=(2r)²-(R-В)²

R²-В²=4r²-R²+2RВ-В²

2r²=R(R-В)

r= √R(R-В)/2 (*)

Пусть В=0→Rmax

R=(√2)/2)R≈0,7R (1)

Sinα=r/R=((√2)/2)*R/R→α=45º (2)

На основании несложных преобразований получено:1)формула для определения радиуса концевой фрезы r(*) 2) доказано, что сфера максимальной глубины будет втом случае, когда B=0 (т.О лежит на поверхности), при этом радиус фрезы д.δ=0,7R(1); 3)ось фрезы должна располагаться по отношению к оси заготовки под углом α=45º. Аналогичными выкладками можно получить формулу для наружных сферических поверхностей (пунзелов).

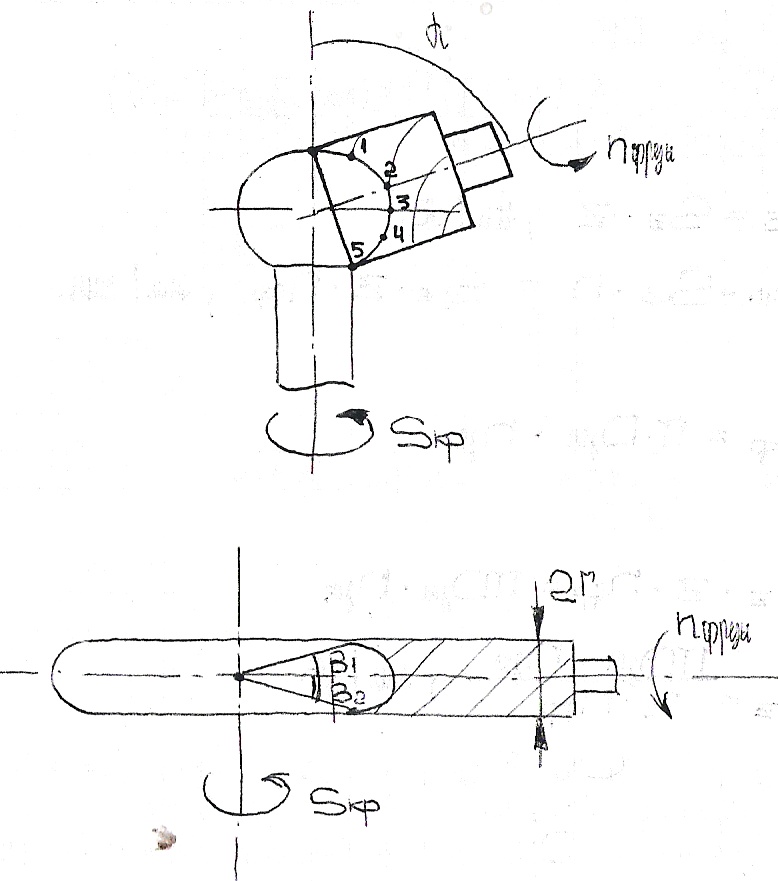
α=π/2-((B1+B2)/2)

rmin=Rsin((B1+B2)/2)

α= π/2 B1=B2

α≠π/2

Теоретически процесс формообразования сферических поверхностей можно завершить за один проход( за один оборот заготовки) без учета врезания. Однако на практике сферические поверхности получают за несколько рабочих ходов или оборотов заготовки в зависимости от величины припуска на мех-ю обработку. При этом процесс фрезерования будет осуществляется с переменной минутной подачей.

Дано: z-число зубьев фрезы, Dфр, Sz-подача на зуб (мм/зуб)(поворот фрезы на 1 зуб), Sоб-подача на оборот (мм/об).

; ;

Sкр-круговая подача на зуб; -длина окр-ти заготовки

;

При обр-ке сферической пов-ти Dзаг будет величиной переменой переменной поэтому процесс резания при фрезеровании сферической пов-ти произв-ся при переменной подаче на зуб Sz, зависящий от Dзаг, на кот-м расположена данная точка сферической пов-ти .