19. Космические скорости. Вывод формулы для расчёта первой космической скорости.

Космическая скорость (первая v₁, вторая v₂, третья v₃ и четвёртая v₄) — это минимальная скорость, при которой какое-либо тело в свободном движении с поверхности небесного тела сможет:

• v₁ — стать спутником небесного тела (то есть способность вращаться по орбите вокруг НТ и не падать на поверхность НТ).

• v₂ — преодолеть гравитационное притяжение небесного тела.

• v₃ — покинуть звёздную систему, преодолев притяжение звезды.

• v₄ — покинуть галактику, преодолев притяжение сверхмассивной черной дыры.

Для вычисления первой космической скорости необходимо рассмотреть равенство центробежной силы и силы тяготения.

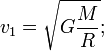
где m — масса объекта, M — масса планеты, G — гравитационная постоянная (6,67259·10⁻¹¹ м³·кг⁻¹·с⁻²), — первая космическая скорость, R — радиус планеты. Подставляя численные значения (для Земли M = 5,97·10²⁴ кг, R = 6 371 км), найдем

 7,9 км/с

Первую космическую скорость можно определить через ускорение свободного падения — так как g = GM/R², то

.

Космические скорости могут быть вычислены и для поверхности других космических тел. Например на Луне v₁ = 1,680 км/с, v₂ = 2,375 км/с

19. Кинетическая и потенциальная энергии.

Рассмотрим случай, когда на тело массой m действует постоянная сила  (она может быть равнодействующей нескольких сил) и векторысилы  и перемещения  направлены вдоль одной прямой в одну сторону. В этом случае работу силы можно определить как A = F∙s.Модуль силы по второму закону Ньютона равен F = m∙a, а модуль перемещения s при равноускоренном прямолинейном движении связанс модулями начальной υ₁ и конечной υ₂ скорости и ускорения а выражением

Отсюда для работы получаем

                          (1)

Физическая величина, равная половине произведения массы тела на квадрат его скорости, называется кинетической энергией тела.

Кинетическая энергия обозначается буквой E_k.

                                                         (2)

Тогда равенство (1) можно записать в таком виде:

A = E_k2 – E_k1.                                                            (3)

Теорема о кинетической энергии:

работа равнодействующей сил, приложенных к телу, равна изменению кинетической энергии тела.

Так как изменение кинетической энергии равно работе силы (3), кинетическая энергия тела выражается в тех же единицах, что и работа,т. е. в джоулях.

Если начальная скорость движения тела массой т равна нулю и тело увеличивает свою скорость до значения υ, то работа силы равна конечному значению кинетической энергии тела:

                                   (4)

Физический смысл кинетической энергии:

кинетическая энергия тела, движущегося со скоростью υ, показывает, какую работу должна совершить сила, действующая на покоящеесятело, чтобы сообщить ему эту скорость.

Потенциальная энергия  — скалярная физическая величина, характеризующая способность некоего тела (или материальной точки) совершать работу за счет его нахождения в поле действия сил.

Потенциальная энергия в поле тяготения Земли вблизи поверхности приближённо выражается формулой:

E_p = mgh,

где E_p — потенциальная энергия тела, m — масса тела, g — ускорение свободного падения, h — высота положения центра масс тела над произвольно выбранным нулевым уровнем.