10.Ряды
421-430.
Исследовать сходимость числового ряда
421.
422.
423.
424.
425.
426.
427.
428.
429.
430.
431-440.
Найти сходимость числового ряда
431.
432.
433.
434.
435.
436.
437.
438.
439.
440.
441-450.
Вычислить определенный интеграл
с точностью до 0,001, разложив подынтегральную
функцию в степенной ряд и затем
проинтегрировав его почленно.
441.
442.
b=1.
443.
444.
445.
446.
447.
448.
449.
450.
b=0,5.
451-460.
Найти три первых, отличных от нуля члена
разложения в степенной ряд решения
у=у(х) дифференциального уравнения
;у),
удовлетворяющего начальному условию
451.
452.
453.
454.
455.
456.
457.
458.
459.
460.
461-470. Разложить данную функцию f(x) в ряд Фурье в интервале (a;b).
461.
f(x)=x+1 в
интервале
462.
f(x)=x
в интервале
(-2;2).
463.
в интервале
464.
в интервале
(-1;1).
4
65.
в интервале
f(x)=
466. f(x)=|1-x| в интервале (-2;2).
467.
f(x)=|x|
в интервале
468. f(x)=x-1 в интервале (-1;1).
469.
f(x)=x
в
интервале
4
70.
f(x)=
в
интервале
11. Уравнения математической физики. Функции комплексного переменного. Операционное исчисление
471-480.
Методом Даламбера найти уравнение
u=u(x;t) формы однородной бесконечной
струны, определяемой волновым уравнением,
если в начальный момент
форма струны и скорость точки струны с
абсциссой х определяются соответственно
заданными u
471.
f(x)=x(2-x), F(x)=e
472.
473.
f(x)=e
,
F(x)=
474.
475.
f(x)=sinx,
476.
477.
478.
479.
480.
481-490.
Представить заданную функцию,
где z=x+iy, в виде
проверить,
является ли она аналитической. Если да,
то найти значение её производной в
заданной точке
481.
482.
483.
484.
485.
486.
487.
488.
489.
490.
491-500.
Разложить функцию f(z) в ряд Лорана в
окрестности точки
и определить область сходимости этого
ряда.
491.
492.
493.
494.
495.
496.
497.
498.
499.
500.
501-510. Методом операционного исчисления найти частное решение дифференциального ура7внения, удовлетворяющее заданным начальным условиям.
501.
х(0)=1,
502.
503.
504.
505.
506.
507.
508.
509.
510.
511-520. Методом операционного исчисления найти частное решение системы дифференциальных уравнений, удовлетворяющее заданным начальным условиям.
511.
х(0)=1; у(0)=0.
5
12.
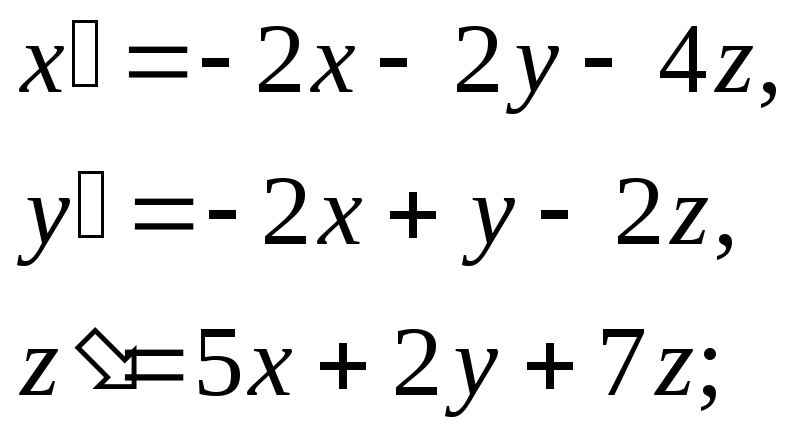
513.
х(0)=2, у(0)=3.
5
14.
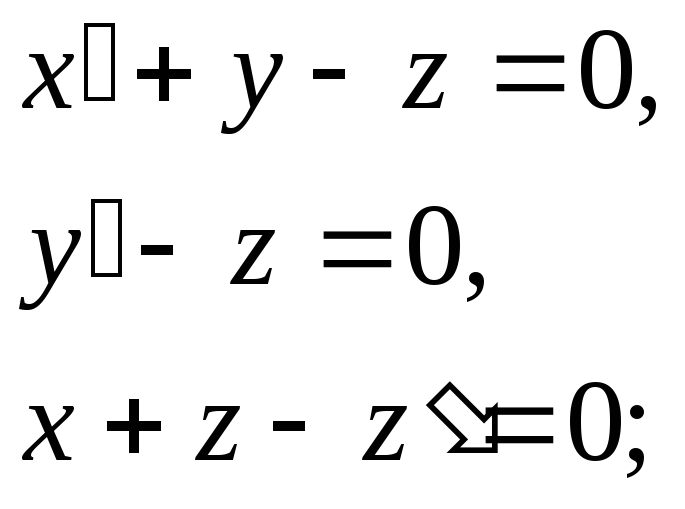х(0)=2, у(0)=1/2, z(0)=5/2.
5
15.
х(0)=1, у(0)=1.
516.
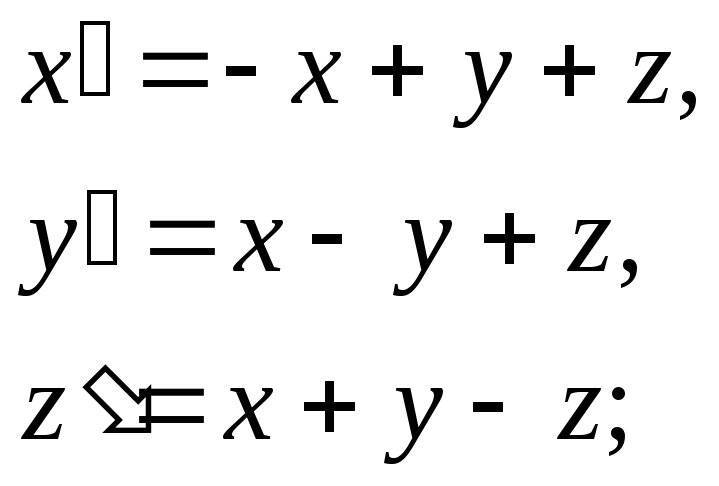х(0)=2, у(0)=2, z(0)=-1.
5
17.
х(0)=0, у(0)=0.
5
18.
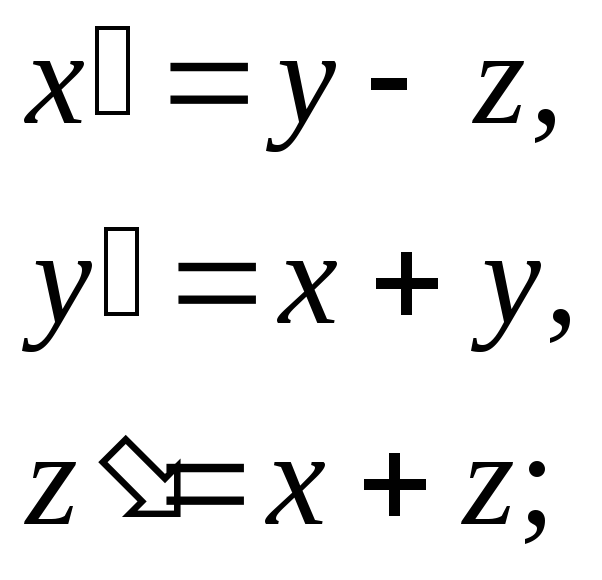х(0)=1, у(0)=2, z(0)=3.
519.
x(0)=1, y(0)=-1.
520.
x(0)=1, y(0)=1.