5. Приложения дифференциального исчисления
191-210.
Исследовать методами дифференциального
исчисления функцию
и, используя результаты исследования,
построить ее график.
191.
192.
193.
194.
195.
196.
197.
198.
199.
200.
201.
202.
203.
204.
.
205.
.
206.
207.
.
208.
209.
210.
211-220.
Найти уравнения касательной, уравнение
нормальной плоскости и вычислить
кривизну линии
в точке
211.
212.
213.
214.
215.
216.
.
217.
218.
219.
220.
221-230.
Определить количество действительных
корней уравнения
отделить эти корни и, применяя метод
хорд и касательных, найти их приближенное
значение с точностью 0,01.
221. a=5, b=7. 222. a=4, b= -6.
223. a=1, b=3. 224. a=2, b= -11.
225. a=1, b= -1. 226. a=1, b= -1.
227. a=4, b=8. 228. a=6, b= -1.
229. a=2, b=4. 230. a=1, b=-4.
6. Дифференциальное исчисление функций нескольких переменных
231-240.
Дана функция
Показать, что
231.
232.
233.
234.
235.
236.
237.
238.
239.
240.
241-250.
Дана функция
и две точки
и
.Требуется:
1) вычислить значение
в точке В; 2) вычислить приближенное
значение
функции в точке В исходя из значения
функции в точке А и заменив приращение
функции при переходе от точки А к
точке В дифференциалом; 3) оценить
в процентах относительную погрешность,
получающуюся при замене приращения
функции ее дифференциалом; 4) составить
уравнение касательной плоскости к
поверхности
в точке
.
241.
А(1;2), В(1,02;
1,96).
242.
А(1;3), В(1,06;
2,92).
243.
А(4;1), В(3,96;
1,03).
244.
А(2;3), В(2,02;
2,97).
245.
А(2;1), В(1,96;
1,04).
246.
А(2;4), В(1,98;
3,91).
247.
А(-1;3), В(-0,98;
2,97).
248.
А(3;2), В(3,05;
1,98).
249.
А(3;4), В(3,04;
3,95).
250.
А(1;2), В(0,97;
2,03).
251-260.
Найти наименьшее и наибольшее значения
функции
в замкнутой области
,
заданной системой неравенств. Сделать
чертеж.
251.
252.
253.
254.
255.
256.
257.
258.
259.
260.
261-270.
Даны функция
,
точка
и вектор
.
Найти: 1) grad z
в точке А; 2) производную в точке А
по направлению вектора а.
261.
А(1;1),
а(2;-1).
262.
А(2;10),
а(3;-4).
263.
А(1;1),
а(3;2).
264.
А(1;1),
а(2;-1).
265.
А(2;1),
а(1;2).
266.
А(2;3),
а(4;-3).
267.
А(1;2), а(5;-12).
268.
А(1;3), а(2;-1).
269.
А(-1;2), а(4;-3).
270.
А(1;1), а(2;1).
271-280.
Экспериментально получены пять значений
функции
при пяти значениях аргумента, которые
записаны в таблице:
-
х
1
2
3
4
5
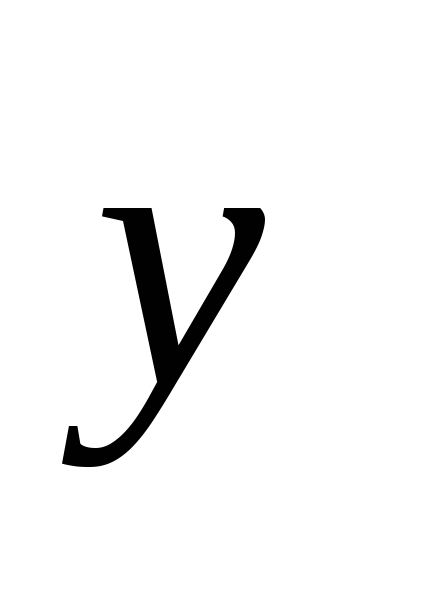
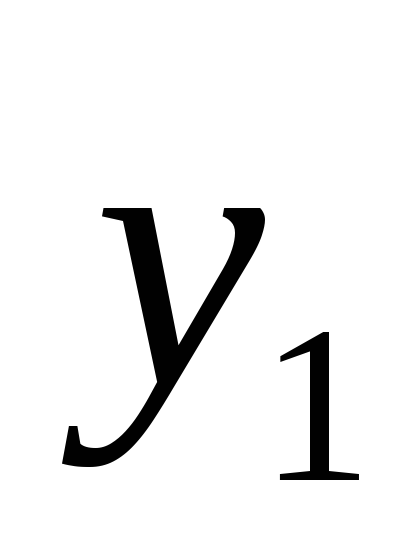
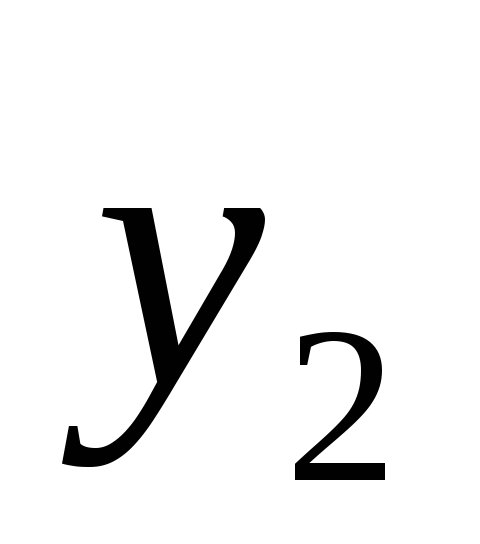
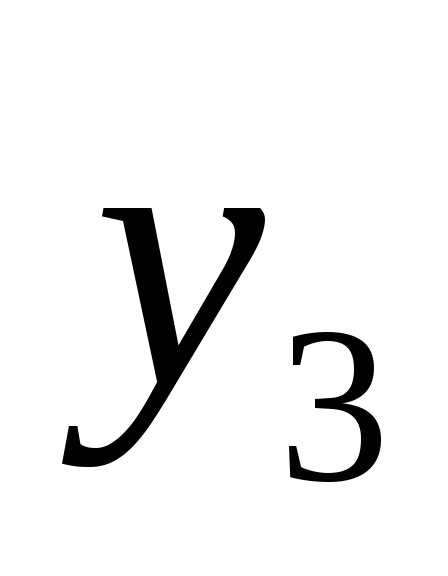
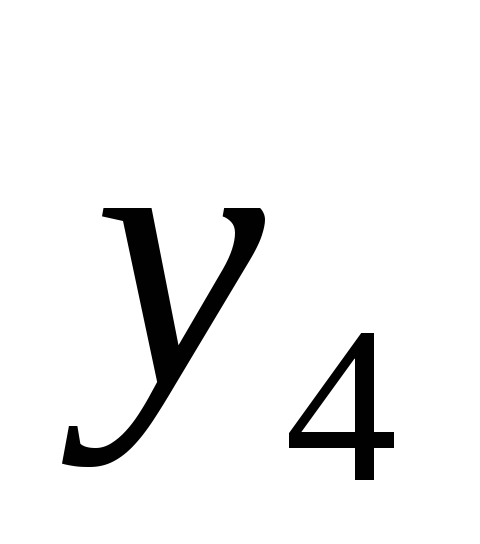
Методом
наименьших квадратов найти функцию
вида
, выражающую приближено (аппроксимирующую)
функцию
.
Сделать чертеж , на котором в декартовой
прямоугольной системе координат
построить экспериментальные точки и
график аппроксимирующей функции
.
271.
3|5, 3|3, 8|1, 8|2 3
272. у||4, 5|5, 5|4, 0|2, 0|2, 5
273. у||4, 7|5, 7|4, 2|2, 2|2 7
274. у||4, 9|5, 9|4, 4|2, 4|2, 9
275. у||5, 1|6, 1|4, 6|2, 6|3, 1
276. у||3, 9|4, 9|3, 4|1, 4|1, 9
277. у||5, 2|6, 2|4, 7|2, 7|3, 2
278. у||5, 5|6, 5|5, 0|3, 0|3, 5
279. у||5, 7|6, 7|5, 2|3, 2|3, 7
280. у||5, 9|6, 9|5, 4|3, 4|3, 9