
- •Інститут безперервної фахової освіти Кафедра економіки та управління
- •Методичні вказівки
- •1.Элементы векторной алгебры и аналитической геометрии
- •2. Элементы линейной алгебры
- •3. Введение в математический анализ
- •4. Производная и ее приложения
- •5. Приложения дифференциального исчисления
- •6. Дифференциальное исчисление функций нескольких переменных
- •7. Неопределенные и определенные интегралы
- •8. Дифференциальные уравнения.
- •9. Кратные, криволинейные и поверхностные интегралы. Векторный анализ
- •10.Ряды
- •11. Уравнения математической физики. Функции комплексного переменного. Операционное исчисление
- •12. Теория вероятностей и математическая статистика
- •13. Математическая статистика.
2. Элементы линейной алгебры
51-60. Дана система линейных уравнений
![]()
 ,
,
![]() ,
,
![]() .
.
Доказать ее совместимость и решить двумя способами: 1) по формулам Крамэра; 2) средствами матричного исчисления
5
 1.
1.
![]() ,
52.
,
52.
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
![]() .
.
5
 3.
3.
![]() ,
54.
,
54.
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
![]() .
.
5
 5.
5.
![]() ,
56.
,
56.
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
![]() .
.

 57.
57.
![]() , 58.
, 58.
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
![]() .
.

 59.
59.
![]() , 60.
, 60.
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
![]() .
.
61-70. Даны два линейных преобразования:

![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Средствами
матричного исчисления найти преобразование,
выражающее
![]() через
через
![]()

 61.
61.
![]() ,
,
![]() ,
,
![]() ,
, ![]() ,
,
![]() .
. ![]() .
.


![]() ,
, ![]() ,
,
62.
![]() ,
, ![]() ,
,
![]()
![]() .
.
![]() .
.
6
 3.
3.
![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
![]() .
. ![]() .
.
6
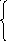 4.
4.
![]() ,
, ![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
![]() .
.![]()
6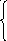
 5.
5. ![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
![]() .
.
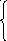

66.
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
![]() .
.
6
 7.
7.
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
![]() .
.


68.
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]()
![]() .
. ![]() .
.
6
 9.
9. ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
![]() .
. ![]() .
.


70. ![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
![]() .
.
71-80. Найти собственные значения и собственные векторы линейного преобразования, заданного в некотором базисе матрицей А.




0 1 0 1 -3 3
71. А= -3 4 0 72. А= -2 -6 13
![]()
 -2
1 2 -1 -4 8
-2
1 2 -1 -4 8



 4 -5
7 5 6 3
4 -5
7 5 6 3
73. А= 1 -4 9 74. А= -1 0 1
-4 0 5 1 2 -1




4 -5 2 2 -1 2
75. А= 5 -7 3 76. А= 5 -3 3
6 -9 4 -1 0 -2




7 0 0 3 1 0
77. А= 10 -19 10 78. А= -4 -1 0
12 -24 13 4 -8 -2




1 -3 4 0 7 4
79. А= 4 -7 8 80. А= 0 1 0
6 -7 7 1 13 0
81-90. Используя теорию квадратичных форм, привести к каноническому виду уравнение второго порядка.
81.
![]()
82.
![]()
83.
![]()
84. ![]()
![]()
85.
![]()
86.
![]()
87.
![]()
88.
![]()
89.
![]()
90.
![]()
91-100.
Дано комплексное число z. Требуется: 1)
записать число z в алгебраической и
тригонометрической формах; 2) найти все
корни уравнения
![]() z
= 0.
z
= 0.
91.
![]()
![]() 92.
92.![]()
93.![]() 94.
94.![]()
![]()
95.![]() 96.
96.![]()
97.![]() 98.
98.![]()
99.![]() 100.
100.![]()
