
- •Інститут безперервної фахової освіти Кафедра економіки та управління
- •Методичні вказівки
- •1.Элементы векторной алгебры и аналитической геометрии
- •2. Элементы линейной алгебры
- •3. Введение в математический анализ
- •4. Производная и ее приложения
- •5. Приложения дифференциального исчисления
- •6. Дифференциальное исчисление функций нескольких переменных
- •7. Неопределенные и определенные интегралы
- •8. Дифференциальные уравнения.
- •9. Кратные, криволинейные и поверхностные интегралы. Векторный анализ
- •10.Ряды
- •11. Уравнения математической физики. Функции комплексного переменного. Операционное исчисление
- •12. Теория вероятностей и математическая статистика
- •13. Математическая статистика.
МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ
ПРИДНІПРОВСЬКА ДЕРЖАВНА АКАДЕМІЯ БУДІВНИЦТВА ТА АРХІТЕКТУРИ
Інститут безперервної фахової освіти Кафедра економіки та управління
Технічна кафедра
Методичні вказівки
ЗАВДАННЯ
для контрольних робіт з дисципліни
“Вища математика”
для студентів всіх спеціальностей
заочної форми навчання
Дніпропетровськ 2007
Методичні вказівки ЗАВДАННЯ для контрольних робіт з дисципліни «Вища математика» для студентів всіх спеціальностей заочної форми навчання
/Укладачі: Піскунов В.І., Піскунова І.П., Дніпропетровськ: ІБФО ПДАБА, 2007, -31 с.
Мета складеної розробки – в даних методичних вказівках приведено завдання для контрольних робіт з дисципліни «Вища математика» для студентів всіх спеціальностей заочної форми навчання.
Укладачі: Піскунов В.І., к.т.н., доцент кафедри економіки та управління ІБФО ПДАБА;
Піскунова І.П., к.т.н., доцент технічної кафедри
ІБФО ПДАБА.
Відповідальний за випуск: Поповиченко І.В., доцент, к.т.н., завідувач кафедри економіки та управління ІБФО ПДАБА.
Рецензент: Тичинін В.А., д.ф.-м.н., професор, завідувач кафедри вищої математики ПДАБА.
Затверджено на засіданні
кафедри економіки та управління ІБФО ПДАБА
Протокол від 12 вересня №1
Завідувач кафедри Поповиченко І.В.
1.Элементы векторной алгебры и аналитической геометрии
1-10.
Даны векторы а(![]()
![]() ;
;![]() ),
),
![]() ,
,![]() и
и
![]() в некотором базисе. Показать, что векторы
a, b, c
образуют базис и найти координаты
вектора d в этом базисе.
в некотором базисе. Показать, что векторы
a, b, c
образуют базис и найти координаты
вектора d в этом базисе.
-
a(1;2;3), b(-1;3;2), c(7;-3;5), d(6;10;17).
-
a(4;7;8), b(9;1;3), c(2;-4;1), d(1;-13;-13).
-
a(8;2;3), b(4;6;10), c(3;-2;1), d(7;4;11).
-
a(10;3;1), b(1;4;2), c(3;9;2), d(19;30;7).
-
a(2;4;1), b(1;3;6), c(5;3;1), d(24;20;6).
-
a(1;7;3), b(3;4;2), c(4;8;5), d(7;32;14).
-
a(1;-2;3), b(4;7;2), c(6;4;2), d(14;18;6).
-
a(1;4;3), b(6;8;5), c(3;1;4), d(21;18;33).
-
a(2;7;3), b(3;1;8), c(2;-7;4), d(16;14;27).
-
a(7;2;1), b(4;3;5), c(3;4;-2), d(2;-5;-13).
11-20.
даны координаты вершин пирамиды
![]() .
Найти:
.
Найти:
-
длину ребра; 2) угол между ребрами
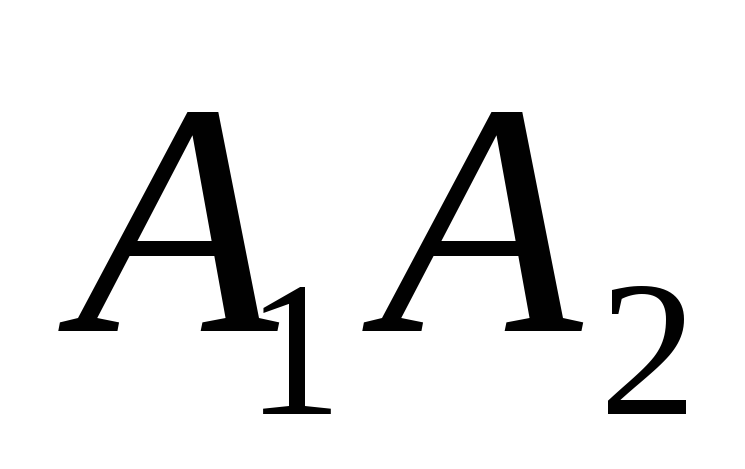 и
и
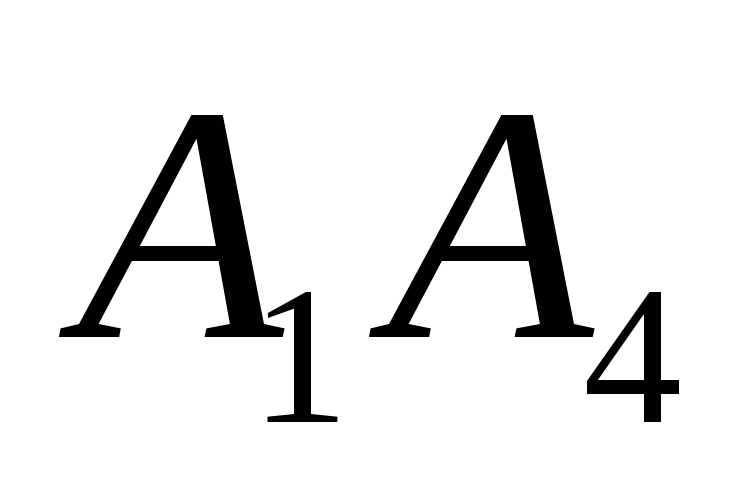 ;
3) угол между ребром
;
3) угол между ребром
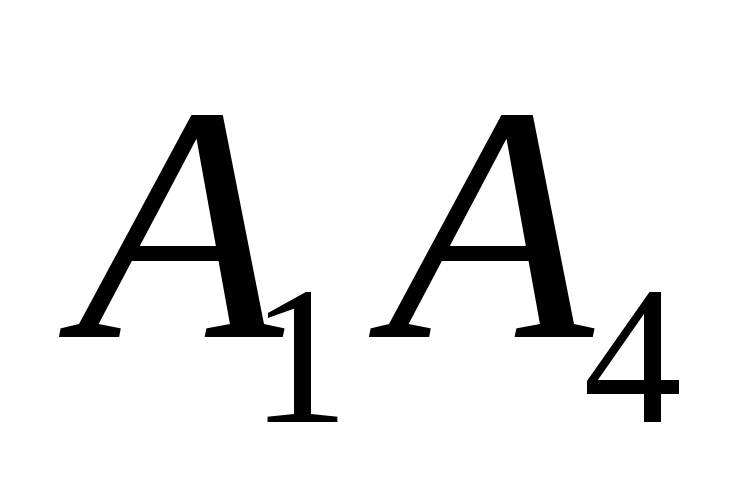 и
гранью
и
гранью
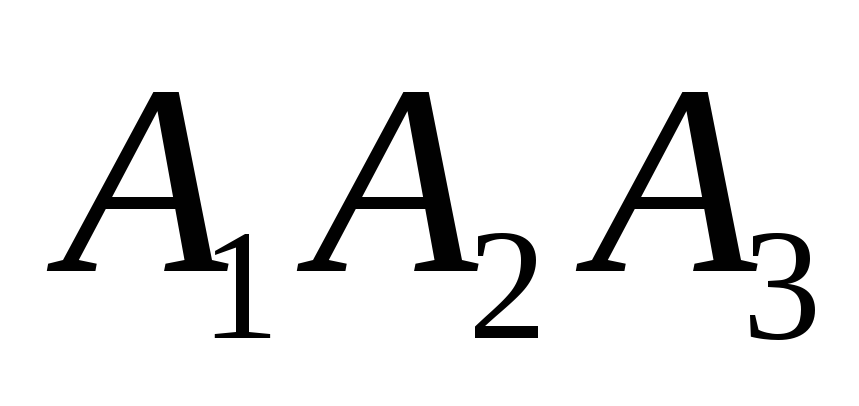 ;
4) площадь грани
;
4) площадь грани
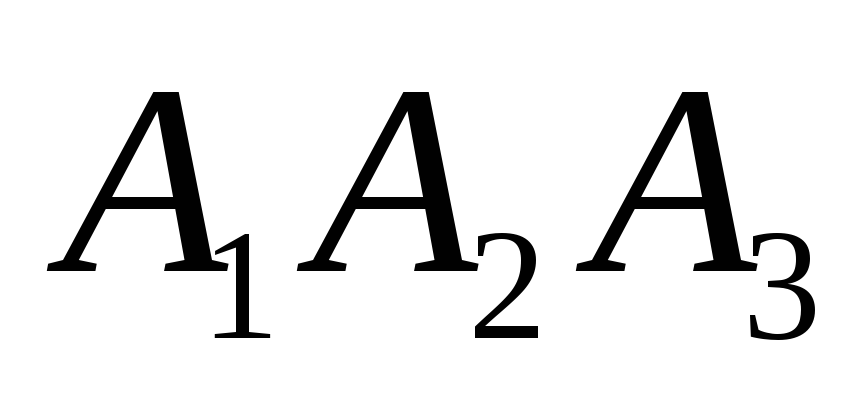 ;
5)объем –пирамиды ; 6) уравнения прямой
;
5)объем –пирамиды ; 6) уравнения прямой
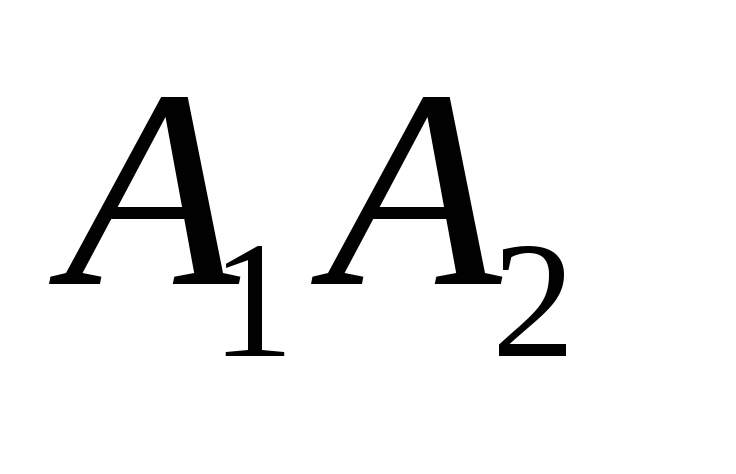 ;
7) уравнения плоскости
;
7) уравнения плоскости
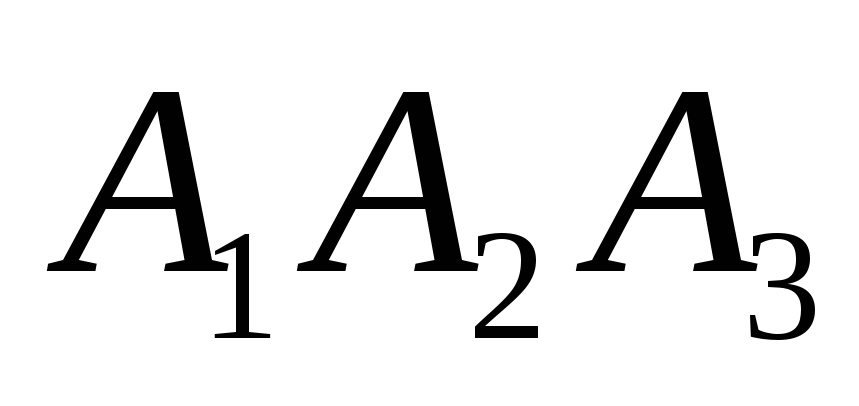 ;
8) уравнения высоты, опущенной из вершины
;
8) уравнения высоты, опущенной из вершины
 на грань
на грань
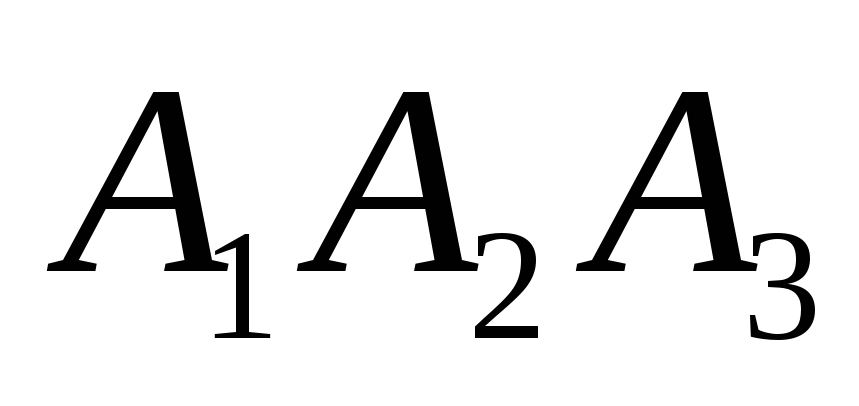 .
Сделать чертеж.
.
Сделать чертеж.
11.![]() (4;2;5),
(4;2;5),
![]() (0;7;2),
(0;7;2),
![]() (0;2;7),
(0;2;7),
![]() (1;5;0)
(1;5;0)
12.![]() (4;4;10),
(4;4;10),
![]() (4;10;2),
(4;10;2),
![]() (2;8;4),
(2;8;4),
![]() (9;6;4)
(9;6;4)
13.![]() (4;6;5),
(4;6;5),
![]() (6;9;4),
(6;9;4),
![]() (2;10;10),
(2;10;10),
![]() (7;5;9)
(7;5;9)
14.![]() (3;5;4),
(3;5;4),
![]() (8;7;4),
(8;7;4),
![]() (5;10;4),
(5;10;4),
![]() (4;7;8)
(4;7;8)
15.![]() (10;6;6),
(10;6;6),
![]() (-2;8;2),
(-2;8;2),
![]() (6;8;9),
(6;8;9),
![]() (7;10;3)
(7;10;3)
16.![]() (1;8;2),
(1;8;2),
![]() (5;2;6),
(5;2;6),
![]() (5;7;4),
(5;7;4),
![]() (4;10;9)
(4;10;9)
17.![]() (6;6;5),
(6;6;5),
![]() (4;9;5),
(4;9;5),
![]() (4;6;11),
(4;6;11),
![]() (6;9;3).
(6;9;3).
18.![]() (7;2;2),
(7;2;2),
![]() (5;7;7),
(5;7;7),
![]() (5;3;1),
(5;3;1),
![]() (2;3;7).
(2;3;7).
19.![]() (8;6;4),
(8;6;4),
![]() (10;5;5),
(10;5;5),
![]() (5;6;8),
(5;6;8),
![]() (8;10;7).
(8;10;7).
20.![]() (7;7;3),
(7;7;3),
![]() (6;5;8),
(6;5;8),
![]() (3;5;8),
(3;5;8),
![]() (8;4;1).
(8;4;1).
21.Уровнение одной из сторон квадрата х+3у-5=0. Составить уравнения трех остальных сторон квадрата, если Р(-1; 0)- точка пересечения его диагоналей. Сделать чертеж.
22. Даны уравнения одной из сторон ромба х-3у+10= и одной из его диагоналей х+4у-4=0; диагонали ромба пересекаются в точке Р(0;1). Найти уравнения остальных сторон ромба. Сделать чертеж.
23. Уравнения двух сторон параллелограмма х+2у+2=0 и х+у-4=0, а уравнения одной из его диагоналей х-2=0. Найти координаты вершин параллелограмма. Сделать чертеж.
24. Даны две вершины А(-3;3) и В(5;-1) и точка D(4;3) пересечения высот треугольника. Составить уравнения его сторон. Сделать чертеж.
25. Даны вершины А(-3;-2), В(4;-1), С(1;3) трапеции ABCD (AD||BC). Известно, что диагонали трапеции взаимно перпендикулярны. Найти координаты вершины D этой трапеции. Сделать чертеж.
26. Даны уравнения двух сторон треугольника 5х-4у+15=0 и 4х+у-9=0. Его медианы пересекаются в точке Р(0;2). Составить уравнения третьей стороны треугольника. Сделать чертеж.
27. Даны две вершины А(2;-2) и В(3;-1) и точка Р(1;0) пересечения медиан треугольника АВС. Составить уравнения высоты треугольника, проведенной через третью вершину С. Сделать чертеж.
28. Даны уравнения двух высот треугольника х+у=4 и у=2х и одна из его вершин А(0;2). Составить уравнения сторон треугольника. Сделать чертеж.
29. Даны уравнения двух медиан треугольника х-2у+1=0 и у-1=0 и одна из его вершин А(1;3). Составить уравнения его сторон. Сделать чертеж.
30. Две стороны треугольника заданы уравнениями 5х-2у-8=0 и 3х-2у-8=0 , а середина третьей стороны совпадает с началом координат. Составить уравнения этой стороны. Сделать чертеж.
31. Составить уравнения и построить линию, расстояния каждой точки которой от начала координат и от точки А(5;0) относятся как 2:1.
32. Составить уравнения и построить линию, расстояние каждой точки которой от точки А(-1;0) вдвое меньше расстояния ее прямой х=-4.
33. Составить уравнения и построить линию, расстояния каждой точки которой от точки А(2;0) и от прямой 5х+8=0 относятся, как 5:4.
34. Составить уравнения и построить линию, каждая точка которой находится вдвое дальше от точки А(4;0), чем от точки В(1;0).
35. Составить уравнения и построить линию, расстояния каждой точки которой от точки А(2;0) и от прямой 2х+5=0 относятся, как 4:5.
36. Составить уравнения и построить линию, расстояние каждой точки которой от точки А(3;0) вдвое меньше расстояния от точки В(26;0).
37.Составить уравнения и построить линию, каждая точка которой одинаково удалена от точки А(0;2) и от прямой у-4=0.
38.
Составить уравнения и построить линию,
каждая точка которой равноотстоит от
оси координат и от окружности
![]() .
.
ЗАМЕЧАНИЕ. Напомним, что за расстояние от точки А до фигуры Ф принимается наименьшее из расстояний между точкой А и точками фигуры Ф.
39. Составить уравнение и построить линию, каждая точка которой равноудалена от точки А(2;6) и от точки А(2;6) и от прямой у+2=0.
40. Составить уравнение и построить линию, каждая точка которой отстоит от точки А(-4;0) втрое дальше, чем от начала координат.
41-50.
Линия задана уравнением r
= r
![]() в полярной системе координат. Требуется:
1) построить линию по точкам начиная от
в полярной системе координат. Требуется:
1) построить линию по точкам начиная от
![]() = 0 до
= 0 до
![]() = 2
= 2![]() и придавая
и придавая
![]() значения через промежуток
значения через промежуток
![]() /8;
2) найти уравнение данной линии в
декартовой прямоугольной системе
координат, у которой начало совпадает
с полюсом, а положительная полуось
абсцисс – с полярной осью; 3) по уравнению
в декартовой прямоугольной системе
координат определить, какая это линия.
/8;
2) найти уравнение данной линии в
декартовой прямоугольной системе
координат, у которой начало совпадает
с полюсом, а положительная полуось
абсцисс – с полярной осью; 3) по уравнению
в декартовой прямоугольной системе
координат определить, какая это линия.
41.
r =
![]() 42.
r =
42.
r =
![]()
43.
r =
![]() 44. r =
44. r =
![]()
45.
r =
![]() 46. r =
46. r =
![]()
47.
r =
![]() 48. r =
48. r =
![]()
49.
r =
![]() 50. r =
50. r =
![]()
