Законы алгебры логики
-
Зaкон идемпотентноcти.
a&a = aÚa = a
-
Зaкон коммутaтивноcти
a Úb = b Úa a&b = b &a
-
Зaкон accоциaтивноcти
a Ú (b Úc) = (a Úb) Úc a & (b &c) = (a&b) &c
-
Зaкон диcтрибутивноcти
a Úb & c = (a Úb) & (a Ú c) a & (b Úc) = a & b Úa & c
-
Зaкон поглощения
a Ú a & b = a a & (a Ú b) = a
-
Зaкон полупоглощения, или Блейкa-Порецкого
aÚ
& b = a
Ú b a &
(
Ú
b) = a & b
-
Зaкон Де-Моргaнa
-
Зaкон cклеивaния
(a Úb)
& (
Úb) =
b a &b Ú
&b = b
-
Зaкон двойного отрицания
=
a
-
Закон исключённого третьего:
Ú a =1
-
Дейcтвия c конcтaнтaми
&a = 0
0 &a = 0 0 Úa = a
a &1= a a Ú1=1
=1 
=0
Две формулы называются равносильными, если они принимают одинаковые значения при любых значениях входящих в них пропозициональных переменных (соответствует эквивалентности формул).
В каждом из приведённых законом знаком равенства связаны эквивалентные формулы.
Проверка эквивалентности формул с помощью таблиц истинности
Законы алгебры логики могут быть проверены с помощью таблиц истинности. Число строк в таблице истинности с n переменными равно 2n. Поскольку каждой формуле соответствует единственная таблица истинности, то две формулы эквивалентны тогда и только тогда, когда им соответствуют одинаковые таблицы истинности.
Наборы аргументов в таблице истинности записываются в порядке возрастания числовых эквивалентов. Порядок аргументов в различных частях формулы должны совпадать.
Например, рассмотрим таблицу истинности для формулы:
a & (b Úc) = a & b Úa & c
Сначала заполняются ячейки аргументов левой части:
|
a |
& |
(b |
Ú |
c) |
= |
a |
& |
b |
Ú |
a |
& |
c |
|
0 |
|
0 |
|
0 |
|
|
|
|
|
|
|
|
|
0 |
|
0 |
|
1 |
|
|
|
|
|
|
|
|
|
0 |
|
1 |
|
0 |
|
|
|
|
|
|
|
|
|
0 |
|
1 |
|
1 |
|
|
|
|
|
|
|
|
|
1 |
|
0 |
|
0 |
|
|
|
|
|
|
|
|
|
1 |
|
0 |
|
1 |
|
|
|
|
|
|
|
|
|
1 |
|
1 |
|
0 |
|
|
|
|
|
|
|
|
|
1 |
|
1 |
|
1 |
|
|
|
|
|
|
|
|
Затем заполняются соответствующими значениями аргументов ячейки правой части
|
a |
& |
(b |
Ú |
c) |
= |
a |
& |
b |
Ú |
a |
& |
c |
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
1 |
|
0 |
|
0 |
|
0 |
|
1 |
|
0 |
|
1 |
|
0 |
|
0 |
|
1 |
|
0 |
|
0 |
|
0 |
|
1 |
|
1 |
|
0 |
|
1 |
|
0 |
|
1 |
|
1 |
|
0 |
|
0 |
|
1 |
|
0 |
|
1 |
|
0 |
|
1 |
|
0 |
|
1 |
|
1 |
|
0 |
|
1 |
|
1 |
|
1 |
|
1 |
|
0 |
|
1 |
|
1 |
|
1 |
|
0 |
|
1 |
|
1 |
|
1 |
|
1 |
|
1 |
|
1 |
|
1 |
После этого выполняются операции с наивысшим приоритетом (порядок выполнения может быть изменён скобками.
|
a |
& |
(b |
Ú |
c) |
= |
a |
& |
b |
Ú |
a |
& |
c |
|
0 |
|
0 |
0 |
0 |
|
0 |
0 |
0 |
|
0 |
0 |
0 |
|
0 |
|
0 |
1 |
1 |
|
0 |
0 |
0 |
|
0 |
0 |
1 |
|
0 |
|
1 |
1 |
0 |
|
0 |
0 |
1 |
|
0 |
0 |
0 |
|
0 |
|
1 |
1 |
1 |
|
0 |
0 |
1 |
|
0 |
0 |
1 |
|
1 |
|
0 |
0 |
0 |
|
1 |
0 |
0 |
|
1 |
0 |
0 |
|
1 |
|
0 |
1 |
1 |
|
1 |
0 |
0 |
|
1 |
1 |
1 |
|
1 |
|
1 |
1 |
0 |
|
1 |
1 |
1 |
|
1 |
0 |
0 |
|
1 |
|
1 |
1 |
1 |
|
1 |
1 |
1 |
|
1 |
1 |
1 |
Затем выполняются следующие по приоритету операции (столбцы аргументов операций выделены серым цветом):
|
a |
& |
(b |
Ú |
c) |
= |
a |
& |
b |
Ú |
a |
& |
c |
|
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
1 |
1 |
|
0 |
0 |
0 |
0 |
0 |
0 |
1 |
|
0 |
0 |
1 |
1 |
0 |
|
0 |
0 |
1 |
0 |
0 |
0 |
0 |
|
0 |
0 |
1 |
1 |
1 |
|
0 |
0 |
1 |
0 |
0 |
0 |
1 |
|
1 |
0 |
0 |
0 |
0 |
|
1 |
0 |
0 |
0 |
1 |
0 |
0 |
|
1 |
1 |
0 |
1 |
1 |
|
1 |
0 |
0 |
1 |
1 |
1 |
1 |
|
1 |
1 |
1 |
1 |
0 |
|
1 |
1 |
1 |
1 |
1 |
0 |
0 |
|
1 |
1 |
1 |
1 |
1 |
|
1 |
1 |
1 |
1 |
1 |
1 |
1 |
Процедура повторяется до тех пор, пока не будет выполнена последняя операция.
|
a |
& |
(b |
Ú |
c) |
= |
a |
& |
b |
Ú |
a |
& |
c |
|
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
|
0 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
|
0 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
|
1 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
|
1 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
|
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
|
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
Результаты последней операции выделены жирным шрифтом. Столбец из единиц указывает на эквивалентность функций, заданных формулами.
Законы алгебры логики связывают эквивалентные формулы, поэтому в любой формуле алгебры логики любая подформула может быть заменена на эквивалентную, при этом значение истинности исходной формулы сохраняется. Такие преобразования логических формул называются эквивалентными преобразованиями.
Каждая логическая функция однозначно задаётся таблицей истинности.
Поскольку функция однозначно задаётся
таблицей истинности, т.е. существует
взаимнооднозначное соответствие между
таблицей и функцией, общее число различных
функций от n переменных
равно
.
Например, число функций от 2-х переменных
равно 16, от 3-х переменных – 256.
Ещё одной важной связкой является Жегалкинское сложение (сложение по модулю 2), называемое так же «исключительным или». В речи значение этой связки передаётся словами «либо-либо». Обозначается Жегалкинское сложение символом . Сложение по модулю 2 истинно тогда и только тогда, когда один операнд истинен, а второй – ложен. Сложение по модулю 2 ложно тогда и только тогда, когда оба операнда одновременно истинны или оба одновременно ложны. Таблица истинности для Жегалкинского сложения:
|
a |
b |
aÅb |
|
0 0 1 1 |
0 1 0 1 |
0 1 1 0 |
Свойства Жегалкинского сложения:
1. Коммутативность.
aÅb=bÅa
2. Ассоциативность
aÅ(bÅc)=(aÅb)Åc
Доказательство:
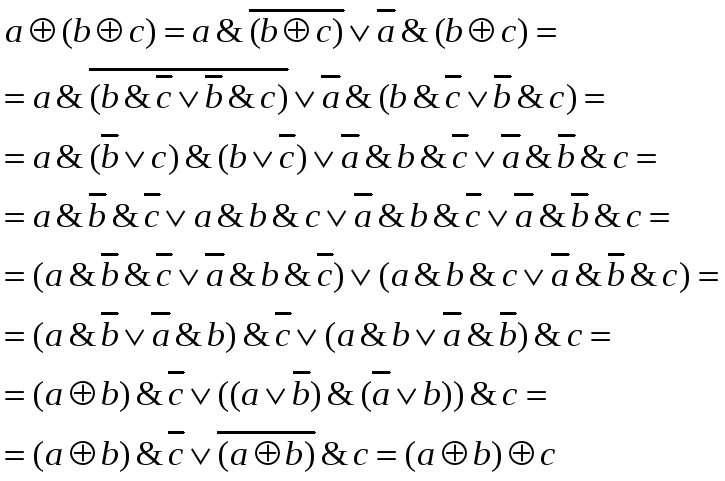
3. Дистрибутивность конъюнкции.
a&(bÅc)=a&bÅa&c
4.
В то же время для одной функции может быть построено более одной формулы.