
- •1 Основные свойства нелинейных цепей
- •1 Аппроксимация вольт-амперной характеристики нелинейной цепи
- •2 Воздействие гармонического колебания на цепь с нелинейным элементом в-54
- •3 Нелинейные преобразователи гармонического сигнала
- •3.1 Нелинейный резонансный усилитель в-56
- •4 Воздействие суммы гармонических колебаний на цепь с нелинейным элементом в-55
- •4.1 Спектральный состав тока при бигармоническом воздействии
- •4.3 Преобразователи частоты в-57
2 Воздействие гармонического колебания на цепь с нелинейным элементом в-54
Пусть на нелинейный элемент с вольтамперной
характеристикой
![]() ,
подаются гармоническое напряжение
сигнала
,
подаются гармоническое напряжение
сигнала
![]() и
постоянное напряжение смещения
и
постоянное напряжение смещения
![]() ,
которое определяет положение рабочей
точки на характеристике (рисунок 6)
,
которое определяет положение рабочей
точки на характеристике (рисунок 6)

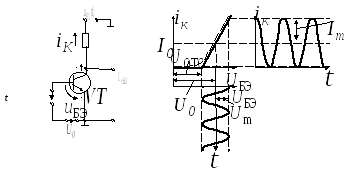
Рисунок 6 − ВАХ нелинейного элемента
На этом же рисунке показана форма тока
в цепи с нелинейным элементом
![]() .
Из-за нелинейности вольтамперной
характеристики формы напряжения и тока
оказываются различными.
.
Из-за нелинейности вольтамперной
характеристики формы напряжения и тока
оказываются различными.
Ток
![]() имеет несинусоидальную форму, т.е. не
является гармоническим колебанием. Мы
уже знаем, что в нелинейном элементе
возникают новые частоты колебаний и
поэтому состав спектра тока
имеет несинусоидальную форму, т.е. не
является гармоническим колебанием. Мы
уже знаем, что в нелинейном элементе
возникают новые частоты колебаний и
поэтому состав спектра тока
![]() отличается
от состава спектра напряжения
отличается
от состава спектра напряжения
![]() .
.
Так как функция является периодической с периодом, она может быть представлена рядом Фурье.
![]()
Это значит, что ток в нелинейном элементе
складывается из постоянной составляющей
и бесконечного числа гармоник с частотами
![]() ,
задача заключается в спектральном
анализе состава тока, т.е. в нахождении
амплитуд спектральных составляющих
,
задача заключается в спектральном
анализе состава тока, т.е. в нахождении
амплитуд спектральных составляющих
![]() ,
в зависимости от постоянного напряжения
смещения и амплитуды переменного
напряжения
,
в зависимости от постоянного напряжения
смещения и амплитуды переменного
напряжения
![]() .
.
Спектральный состав тока при степенной аппроксимации
![]() ,
,
где значения амплитуд спектральных
составляющих
![]() определяются выражениями, заключенными
в формуле (8) в скобки.
определяются выражениями, заключенными
в формуле (8) в скобки.
Спектральный состав тока при
кусочно-линейной аппроксимации. На
рисунке 7 показана форма тока в цепи с
нелинейным элементом при кусочно-линейной
аппроксимации его характеристики
функцией когда на вход подается напряжение
![]() .
.
График тока имеет характерный вид
косинусоидальных импульсов с отсечкой.
Половина той же части периода, в течение
которой протекает ток, называется углом
отсечки. На рисунке 7 угол отсечки
обозначен
![]() и показан как на графике тока, так и на
графике напряжения. Измеряется угол
отсечки в радианах или в градусах.
и показан как на графике тока, так и на
графике напряжения. Измеряется угол
отсечки в радианах или в градусах.

Рисунок 7 − Форма тока в цепи с нелинейным элементом
3 Нелинейные преобразователи гармонического сигнала
3.1 Нелинейный резонансный усилитель в-56
Нелинейный резонаторный усилитель
изображен на рисунке 9. На входе его
действует переменное напряжение
![]() и постоянное напряжение смещения
и постоянное напряжение смещения
![]() .
Будем полагать, что вольтамперная
характеристика
.
Будем полагать, что вольтамперная
характеристика
![]() ,
т. е. зависимость тока коллектора от
напряжения на участке «база-эмиттер»,
достаточно точно представляется
кусочно-линейной функцией. Если на входе
нелинейного элемента (транзистора)
действует напряжение
,
т. е. зависимость тока коллектора от
напряжения на участке «база-эмиттер»,
достаточно точно представляется
кусочно-линейной функцией. Если на входе
нелинейного элемента (транзистора)
действует напряжение
![]() не выходящее за приделы линейного
участка, то ток в цепи коллектора
не выходящее за приделы линейного
участка, то ток в цепи коллектора
![]()
будет, как и входное напряжение, гармоническим (смотри рисунок 10 б).
Если же амплитуда переменного напряжения велика, так что напряжение «выходит» за рамки линейного участка (подобная картина показана на рисунке 7), то ток в цепи коллектора имеет форму косинусоидальных импульсов с отсечкой. Резонансный контур настроен на частоту первой гармоники тока, т.е. на частоту входного сигнала.

Рисунок 9 − Нелинейный резонаторный усилитель
Сопротивление параллельного контура
на этой частоте велико, а на частотах
гармоник
![]() ,
очень мало, так что высшие гармонические
составляющие практически не дают вклада
в выходной сигнал
,
очень мало, так что высшие гармонические
составляющие практически не дают вклада
в выходной сигнал
![]() и
и
![]() ,
где
,
где
![]() −
амплитуда первой гармоники тока
коллектора
−
амплитуда первой гармоники тока
коллектора
![]() ,
,
![]() −
сопротивление параллельного контура
на резонансной частоте
−
сопротивление параллельного контура
на резонансной частоте
![]() .
.
а) ―транзисторный резистивный каскад;
б) ―ток и напряжение на входе нелинейного элемента
Рисунок 10 − Нелинейный резонаторный усилитель с резистивной нагрузкой
Выходное напряжение
![]()
практически будет косинусоидальным (т. е. гармоническим).
Резонансный умножитель частоты
Схема резонансного умножителя частоты
отличается от нелинейного резонансного
усилителя (смотри рисунок 9) только тем,
что колебательный контур в выходной
цепи настраивается на частоту одной из
высших гармоник входного сигнала.
Амплитуда выходного сигнала умножителя
при кусочно-линейной аппроксимации
равна
![]() ,
а выходной сигнал
,
а выходной сигнал
![]() имеет частоту в
имеет частоту в
![]() раз более высокую, чем у входного сигнала
раз более высокую, чем у входного сигнала
![]()
При больших
![]() функции
функции
![]() имеют
небольшие значения, поэтому важно
выбрать угол отсечки
имеют
небольшие значения, поэтому важно
выбрать угол отсечки
![]() ,
при котором значение соответствующей
функции Берга максимально. Существует
оптимальный угол отсечки. При таком
угле отсечки
,
при котором значение соответствующей
функции Берга максимально. Существует
оптимальный угол отсечки. При таком
угле отсечки
![]() амплитуда выходного напряжения получается
наибольшей.
амплитуда выходного напряжения получается
наибольшей.
Умножители частоты применяются в
радиотехнике для получения высокочастотных
стабильных колебаний, когда в распоряжении
имеется весьма стабильный низкочастотный
генератор. Если отклонение частоты
![]() ,
генерируемой низкочастотной схемой,
составляет
,
генерируемой низкочастотной схемой,
составляет
![]() ,
то относительная нестабильность частоты
равна
,
то относительная нестабильность частоты
равна
![]() .
В умножителе частоты
.
В умножителе частоты
![]() вместо частоты получаем частоту
вместо частоты получаем частоту
![]() ,
а относительная нестабильность остается
такой же, как и у низкочастотного
генератора.
,
а относительная нестабильность остается
такой же, как и у низкочастотного
генератора.
