Нелинейные цепи

1 Основные свойства нелинейных цепей

Все цепи, рассматриваемые до сих пор, относились к классу линейных систем. Элементы таких цепей и являются постоянными и не зависят от воздействия. Линейные цепи описываются линейными дифференциальными уравнениями с постоянными коэффициентами.

Свободные колебания напряжения на емкости в последовательном − колебательном контуре удовлетворяют дифференциальному уравнению

.

Если элементы электрической цепи и зависят от воздействия, то цепь описывается нелинейным дифференциальным уравнением и является нелинейной. Например, для колебательного −контура, сопротивление которого зависит от напряжения , получим

Такой колебательный контур является нелинейным. Элемент электрической цепи, параметры которого зависят от воздействия, называется нелинейным. Различают резистивные и реактивные нелинейные элементы.

Для нелинейного резистивного элемента характерна нелинейная связь между током и напряжением , т. е. нелинейная характеристика . Наиболее распространенными резистивными нелинейными элементами являются ламповые и полупроводниковые приборы, используемые в радиотехнике для усиления и преобразования сигналов.

На рисунке 1 приведены ВАХ типовых нелинейных резисторов и их условные обозначения: полупроводникового (а) и туннельного (б) диодов, биполярного (в) и полевого (г) транзисторов. Здесь , и − соответственно напряжение, приложенное к участку «база−эмиттер», и токи базы и коллектора биполярного транзисторов; и − соответственно напряжение, приложенное к участку, «затвор−исток» и ток стока полевого транзистора.

Для резистивных нелинейных элементов важным параметром является сопротивление, которое в отличие от нелинейных резисторов не является постоянным, а зависит от того, в какой точке ВАХ оно определяется. На рисунке 2 изображена ВАХ нелинейного элемента. Можно определить сопротивление как

,

где − приложенное к нелинейному элементу постоянное напряжение; − протекающий по цепи постоянный ток.

Это сопротивление постоянному току (или статическое). Оно зависит от приложенного напряжения. Пусть на нелинейный элемент действует напряжение , причем амплитуда переменной составляющей достаточно мала (рисунке 2), так что тот небольшой участок ВАХ, в пределах которого действует переменное напряжение, можно считать линейным.

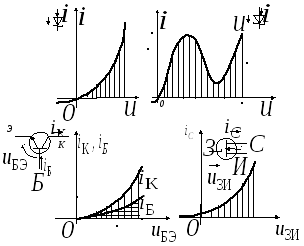
а) б)

в) г)

а) − полупроводникового транзистора; б) − тунельного транзистора;

в) − биполярного транзистора; г) − полевого транзистора;

Рисунок 1 − Вольтамперные характеристики

Тогда ток, протекающий через нелинейный элемент, повторит по форме напряжение: . Определим сопротивление как отношение амплитуды переменного напряжения к амплитуде переменного тока (на графике это отношение приращения напряжения к приращению тока ):

Это сопротивление называется дифференциальным (динамическим) и представляет собой сопротивление нелинейного элемента переменному току малой амплитуды.

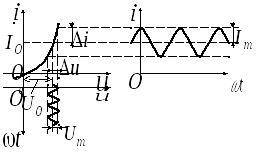
Рисунок 2 − ВАХ нелинейного элемента

Обычно переходят к пределу этих приращений и определяют дифференциальное сопротивление в виде. Иногда удобно пользоваться понятием дифференциальной крутизны (проводимости)

.

Приборы, имеющие падающие участки на ВАХ (см. рисунок 1, б), называются приборами с отрицательным сопротивлением, т. к. на этих участках производные и .

К нелинейным реактивным элементам относятся нелинейная емкость и нелинейная индуктивность. Примером нелинейной емкости может служить любое устройство, обладающее нелинейной вольт-кулонной характеристикой (например, вариконд или варикап). Нелинейной индуктивностью является катушка с ферромагнитным сердечником, обтекаемая сильным током, доводящим сердечник до магнитного насыщения.

Одной из важнейших особенностей нелинейных цепей является то, что в них не выполняется принцип наложения. Поэтому невозможно предсказать результат воздействия суммы сигналов, если известны реакции цепи на каждое слагаемое воздействия. Из сказанного вытекает непригодность нелинейных цепей временного (интеграл наложения) и спектрального (преобразование Фурье) методов, которые применялись в теории линейных цепей.

Действительно, пусть вольт-амперная характеристика (ВАХ) нелинейного элемента описывается выражением . Если на такой элемент действует сложный сигнал , то отклик отличается от суммы откликов на действие каждой составляющей в отдельности наличием каждой составляющей в отдельности , которая появляется только в случае одновременного воздействия обеих составляющих.

Рассмотрим вторую отличительную особенность нелинейных цепей. Пусть , где и − амплитуды напряжений и . Тогда ток в нелинейном элементе с ВАХ будет иметь вид:

На рисунке 3 построены спектры напряжения (а) и тока (б). Все спектральные компоненты тока оказались новыми, не содержащимися в напряжении. Таким образом, в нелинейных цепях возникают новые спектральные компоненты. В этом смысле нелинейные цепи обладают гораздо большими возможностями, чем линейными, и широко используются для преобразований сигналов, связанных с изменением их спектров.

При изучении теории нелинейных цепей можно не учитывать устройство нелинейного элемента и опираться только на его внешние характеристики подобно тому, как при изучении теории линейных цепей не рассматривают устройство резисторов, конденсаторов и катушек и пользуются только их параметрами , и .

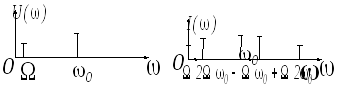
а) б)

а) − напряжения; б) − тока

Рисунок 3 − Спектры напряжения и тока в нелинейном элементе