Лекция 4. Принципы, виды и методы измерений

Измерения как экспериментальные процедуры определения значений измеряемых величин весьма разнообразны. Это объясняется множеством измеряемых величин, раз­личным характером их изменения во времени, различными требованиями к точности из­мерений и т. д. Основными характеристиками измерений являются: принцип измерений, вид измерений, метод измерений , а также погрешность измерений.

1. Принцип измерения

Принцип измерения - физическое явление или совокупность явлений, положенных в основу измерений. Например, измерение массы тела при помощи взвешивания с исполь­зованием силы тяжести, пропорциональной массе. Другие примеры - измерение темпе­ратуры с использованием термоэлектрического эффекта, оптические измерения на основе фотоэлектрического эффекта и др.

2. Виды измерений

По способу получения числового значения измеряемой величины все измерения делятся на прямые и непрямые. Различают три вида непрямых измерений: косвенные совместные и совокупные.

Прямым называют измерение, при котором искомое значение одной величины находят непосредственно из опытных данных. Простейшими примерами прямых изме­рений являются измерения длины линейкой с делениями, температуры – термомет­ром, объема жидкости—мерным сосудом, электрического напряжения - вольтметром и т. д. Прямые измерения составляют основу более сложных видов измере­ний. Уравнение прямых измерений имеет вид:

X = CN_x,

где Х – значение измеряемой величины в принятых для нее единицах измерения;

С - цена деления шкалы или единичного показания цифрового отсчетного устройства в единицах измеряемой величины;

N_x – отсчет в делениях шкалы измерительного устройства.

Из всех методов прямых измерений можно выделить несколько основных: метод непосредственной оценки, дифференциальный метод, нулевой метод и метод совпадений. Прямые измерения лежат в основе косвенных и совокупных измерений.

Косвенными называют измерения, результат которых определяют на основании прямых измерений величин, связанных с измеряемой величиной известной зависимостью.

Уравнение косвенных измерений имеет вид:

Y = f(x₁, x₂, …, x_n),

г де Y – искомая величина, являющаяся функцией аргументов x₁, x₂, …, x_n, измерен­ных прямым методом. Например, площадь круга можно определить по известной формуле после прямого измерения диаметра d этого круга. Электрическое сопротив­ление некоторого резистора можно определить по результатам измерений проходящего через него тока и падения напряжения на этом резисторе. Находить зна­чения некоторых вели­чин легче и проще путем косвенных измерений, чем путем прямых. Иногда прямые изме­рения практически невозможно осуществить, как например, изме­ре­ние плотности твердо­го тела, определяемой обычно по результатам измерений объема и массы. Косвен­ные из­мерения некоторых величин позволяют получить значительно более точные ре­зультаты, чем прямые измерения.

Совокупные измерения - одновременные измерения нескольких одноименных вели­чин, при которых искомые значения величин находят решением следующей системы урав­­нений, составленных по результатам прямых измерений различных сочетаний этих величин:

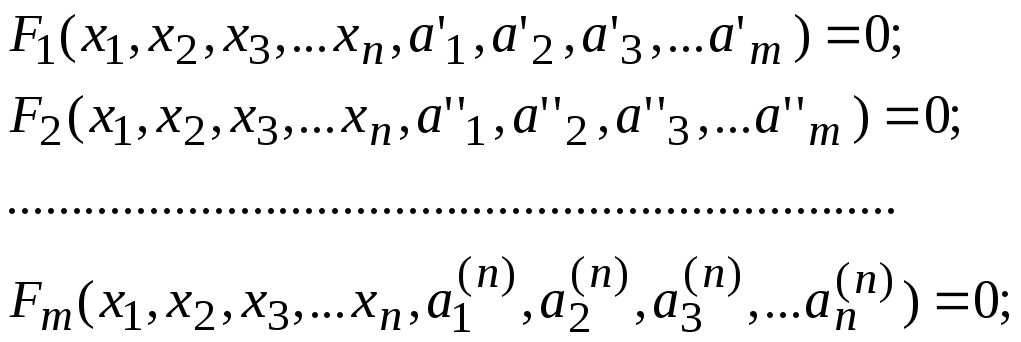
где -- искомые величины,

—значения изме­рен­ных величин.

Пример совокупных результатов: измерение сопротивлений, соединенных треуго­ль­ником. Сначала измеряют сопротивления между различными вершинами треугольника, а затем по результатам трех измерений и на основании уравнений связи определяют сопротивления резисторов.

Другой пример совокупных измерений – поверка набора гирь. Пусть необходимо определить действительное значение массы каждой гири из набора 1, 2, 3 и 5 кг. Если в распоряжении имеются равнопле­чие весы , образцовая гиря 1 кг и образцовые мелкие гири, то можно поступить следующим образом. Последо­ва­тельно производятся четыре измерения массы поверяемых гирь на равноплечих весах. Результаты измерения фикси­руются в виде уравнений:

х₁ = 1 кг + m₁;

х₂ = 1 кг +х₁ + m₂;

х₃ = 1 кг +х₂ + m₃;

х₅ = 1 кг +х₁ +х₃ + m₅,

где х₁, х₂, х₃, х₅ – искомые массы гирь;

m₁, m₂, m₃, m₅ - массы мелких гирь, необходимых для уравновешивания весов;

1 кг – масса образцовой гири.

В этой системе из четырех уравнений имеются четыре неизвестных х₁, х₂, х₃, х₅ и пять известных величин – одна образцовая масса и четыре поправочных переменных m₁, m₂, m₃, m₅. Задача решается путем решения системы уравнений.

Совместные измерения — одновременные измерения двух или нескольких неодно­именных величин для нахождения зависимости между ними. Пример совместного измере­ния: опре­деление зависимости сопротивления некоторого проводника от температуры измеряя сопротивление резистора при трех различных темпера­ту­рах, составляют систему из трех уравнений

из которых находят параметры Ro, А, В зависимости R(t).