Тогда, вычисляя а(хi) первым способом, получим:

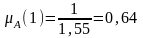
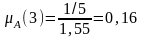
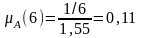
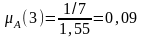
A={<0,64/1>, <0,16/3>, <0,11/6>, <0,09/8>}

Нормируем функцию

A={<1/1>, <0,26/3>, <0,17/6>, <0,14/8>}

Функция принадлежности на универсальной шкале

Обычно функции принадлежности формируются на основе данных, получаемых от специалистов в моделируемой предметной области (экспертов). При этом функция принадлежности строится на предметной шкале. Если пределы универсального множества Х изменяются, придется вновь прибегать к опросу экспертов для построения функций принадлежности. Для некоторых задач можно избежать этого этапа с помощью использования универсальных шкал. Для этого используется преобразование, отображающее значения функции принадлежности на отрезок [0;1]. Такое преобразование, в свою очередь, представляет собой некоторую функцию, которая строится также с помощью экспертов.

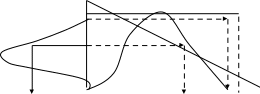
При грубом приближении в качестве этой функции можно использовать прямую (f на рис.8). Функции принадлежности на универсальной шкале изображается вертикально. Значения, расположенные на оси Х, отображаются с помощью функции f на вертикальную ось, отрицательная часть горизонтальной оси превращается в ось значений функции принадлежности. Так в примере на рис.8 функции приведено отображение функций принадлежности на универсальную шкалу. В этом случае при изменении границ универсального множества достаточно выполнить обратное преобразование для получения функций принадлежности в новых границах, не привлекая вновь к этой процедуре экспертов.

f

1 1

a

1 a 0 Х₁

Рис.8. Функция принадлежности на универсальной шкале

Нечеткая переменная – это тройка <a, X,C_a>, где

a – наименование нечеткой переменной,

X – универсальное множество,

C_a – нечеткое множество, определенное на множестве X.

Арифметические операции над нечеткими переменными

Определение операций над нечеткими множествами рассмотрим для случая двух нечетких переменных A₁ и A₂, которые заданы своими трапециевидными функциями принадлежности вида

A₁ = ( , ),

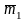A₂ = ( , ).

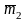Результатом операции будет также нечеткая переменная A=( , ), которая также имеет трапециевидную функцию принадлежности, параметры которой определяются в зависимости от вида арифметической операции (таблица 2).

Таблица 2

Тип операции	Зависимости параметров функций принадлежности
	, , , .
	, , , .
	, , , .
	, , , .

ПРИМЕР.

Лингвистическая переменная

Лингвистической переменной называется кортеж < , Т, Х, G, М >, где  - наименование лингвистической переменной, Т - множество нечетких понятий, определенных на универсальном множестве Х, G - синтаксическая процедура, позволяющая генерировать новые осмысленные термы (грамматика), М - семантическая процедура, которая каждое новое значение лингвистической переменной, образуемое с помощью G, превращает в нечеткую переменную путем формирования нечеткого множества. Лингвистическая переменная принимает значения из множества Т (терм-множество).

Для формирования лингвистической переменной необходимо:

1. Определить имя лингвистической переменной.

2. Определить имена нечетких переменных, являющихся значениями лингвистической переменной и элементами терм множества T = {t_i} (i=1,m).

3. Определить универсальное множество X.

4. Задать на универсальном множестве X нечеткие множества С_i, определяющие нечеткие переменные с именами t_i.

5. Построить грамматику, синтаксическую процедуру G, позволяющую генерировать новые осмысленные термы {t*_j} (i=1,n).

6. Сформировать семантическую процедуру М, которая для каждого нового значения лингвистической переменной, образуемого с помощью G, строит функцию принадлежности нечеткого множества нечеткой переменной с именем t*_j, i=1,n.

Пример.

Построить лингвистическую переменную, соответствующую понятию «размер дохода на одного члена семьи».

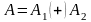
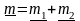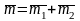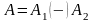
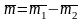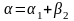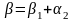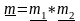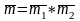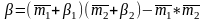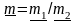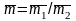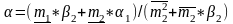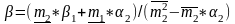8