
- •4. Ускорение
- •5. Обратная задача кинематики
- •6. Движение по окружности
- •2. Сила электрического взаимодействия.
- •4. Силы
- •1. Сила гравитационного взаимодействия.
- •3. Силы упругости.
- •3. Уравнение динамики вращательного движения
- •4. Теорема Штейнера
- •Xoy, совпадает по форме с уравнением вращательного движения тела вокруг закрепленной оси (3.9):
- •6. Закон сохранения момента импульса
- •2. Теорема о кинетической энергии
- •4. Потенциальная энергия
- •3. Потенциальные силы
- •5. Закон сохранения энергии
- •4. Физический маятник.
- •3. Математический маятник.
- •1. Затухающие колебания.
- •1. Плоская монохроматическая волна
- •4. Дисперсия
- •1. Постулаты сто.
- •1. Постулат относительности.
- •2. Постулат постоянства скорости света.
- •3. Следствия из преобразований Лоренца.
- •1. Второй закон Ньютона в сто.
- •3. Связь энергии и импульса.
- •4. Эквивалентность массы и энергии
- •2. Абсолютная температура. Макроскопические параметры
Xoy, совпадает по форме с уравнением вращательного движения тела вокруг закрепленной оси (3.9):
![]()
Последнее утверждение (его можно строго доказать!) выглядит довольно странным, так как уравнение (3.9) было написано относительно ИСО, система же отсчета (ось OZo), в которой происходит вращение тела, не является инерциальной, так как центр масс тела движется с ускорением а0. Тем не менее это так, и связан
этот факт именно с тем, что мы выбрали в качестве точки О при рассмотрении поступательного движения центр масс тела. При решении конкретных задач уравнения (3.12) и (3.13) следует еще дополнить кинематическими
![]()

Для этого воспользуемся условием отсутствия проскальзывания цилиндра. Если нет проскальзывания, то точка А (см. рис.3.7), находящаяся на поверхности цилиндра и соприкасающаяся с наклонной плоскостью, в любой момент времени неподвижна в системе XOY. С другой стороны, эта точка движется

![]()
![]()
![]()

силы: сила тяжести Мд, реакции опоры N и сила
трения покоя ?. Уравнение поступательного движения в проекциях на оси ОХ и OY имеет вид:
![]()
Подставляя (3.16) в (3.15) и исключая f с помощью (3.14), окончательно получим
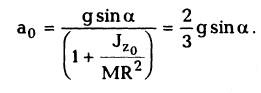
6. Закон сохранения момента импульса
В заключение отметим, что если тело вращается вокруг закрепленной в пространстве оси, и на него не действуют внешние силы, то из

![]()
![]()
![]()
относительно оси OZq (направленной от нас) выглядит следующим образом:
цилиндра относительно оси OZq и R (радиус
цилиндра) - плечо силы f . Так как силы тяжести и реакции опоры проходят через ось OZq, их

17
Лекция 4. РАБОТА И ЭНЕРГИЯ
Работа постоянной и переменной силы; теорема о кинетической энергии; потенциальные силы; потенциальная энергия; закон сохранения энергии.
 1.
Работа постоянной и переменной
силы
1.
Работа постоянной и переменной
силы
Из школьного курса физики мы знаем, что при движении частицы по прямолинейной траектории постоянная по величине и направлению сила
f совершает над частицей работу
![]()
где f — модуль силы, As — отрезок прямолинейного пути и а — угол между направлениями силы и перемещения. Выражение (4.1) можно записать в виде
![]()
Интеграл в правой части (4.3) называется криволинейным интегралом 1-го рода. Из (4.3) следует, что при движении частицы из точки 2 в точку 1 по той же самой траектории работа силы
f :
![]()
Вспомним теперь, что ds = |dr|, где dr — вектор бесконечно малого перемещения. Тогда
![]()
где fs — проекция силы на перемещение. Из определения работы видно, что последняя может быть как положительной, когда fs>0, так и отрицательной, когда fs<0, и равной нулю, когда сила перпендикулярна перемещению.
Спрашивается, как найти работу силы f , которая в разных точках траектории движения различна по величине и направлению (говорят, что частица движется в неоднородном силовом
поле f(x,y,z))r а сама траектория криволинейна (см. рис.4.1).

Поступают следующим образом. Всю траекторию от начальной точки 1 до конечной 2 разбивают на бесконечно малые участки ds, которые в силу своей бесконечной малости можно считать прямолинейными. Опять же в силу того, что путь ds бесконечно малый, можно считать, что
сила f остается постоянной как по величине, так и по направлению на этом участке пути ds. Тогда,
![]()
Работа же силы f на конечном участке траектории от начальной точки 1 до конечной 2
согласно (4.1), элементарная работа силы f на пути ds
![]()
Последний интеграл называется
криволинейным интегралом 2-го рода,
вычисление которого, как правило, проще, чем вычисление криволинейного интеграла 1-го рода.
Мощностью силы f называется работа силы в единицу времени.
Так как за бесконечно малое время dt сила
совершает работу dA = fsds = fdr, то мощность
![]()
