
- •Часть 2
- •Часть 2
- •Содержание
- •Введение
- •1. Требования к выполнению контрольной работы
- •2. Основные формулы, термины и определения
- •Раздел "Интегральное исчисление функции одной переменной"
- •3. Примерный вариант контрольной работы №2 Задание № 1 по теме "Дифференциальное исчисление функции одной переменной"
- •Задание № 2 по теме "Интегральное исчисление функции одной переменной"
- •4. Решение примерного варианта контрольной работы Задание № 1 по теме "Дифференциальное исчисление функции одной переменной"
- •Задание № 2 по теме "Интегральное исчисление функции одной переменной"
- •5. Варианты контрольных работ для слушателей зачного отделения
- •Контрольная работа № 2
- •Вариант № 1
- •Задание № 1
- •Задание № 2
- •Вариант № 4 Задание № 1
- •Задание № 2
- •Вариант № 5 Задание № 1
- •Задание № 2
- •Вариант № 6 Задание № 1
- •Задание № 2
- •Вариант № 7 Задание № 1
- •Задание № 2
- •Вариант № 8 Задание № 1
- •Задание № 2
- •Вариант № 9 Задание № 1
- •Задание № 2
- •Вариант № 10 Задание № 1
- •Задание № 2
- •Рекомендуемая литература
- •Образец оформления титульного листа контрольной работы
- •Часть 2
Вариант № 5 Задание № 1
-
Найти пределы функции
 при различных значениях ɑ (не применяя
правила Лопиталя):
при различных значениях ɑ (не применяя
правила Лопиталя):
![]() ɑ
= 2; ɑ = 4; ɑ
.
ɑ
= 2; ɑ = 4; ɑ
.
-
Вычислить производную функций:
1).
![]() ;
;
2).
![]() .
.
-
Вычислить y' в точке x0 :
 ; x0
= – 5.
; x0
= – 5. -
Найти экстремумы функции
 .
. -
Найти наибольшее и наименьшее значение функции y на отрезке [ – 6, – 1]:

-
Вычислить
 ,
используя правило Лопиталя:
,
используя правило Лопиталя:
![]() ; ɑ
= – 1.
; ɑ
= – 1.
Задание № 2
-
Вычислить неопределенный интеграл
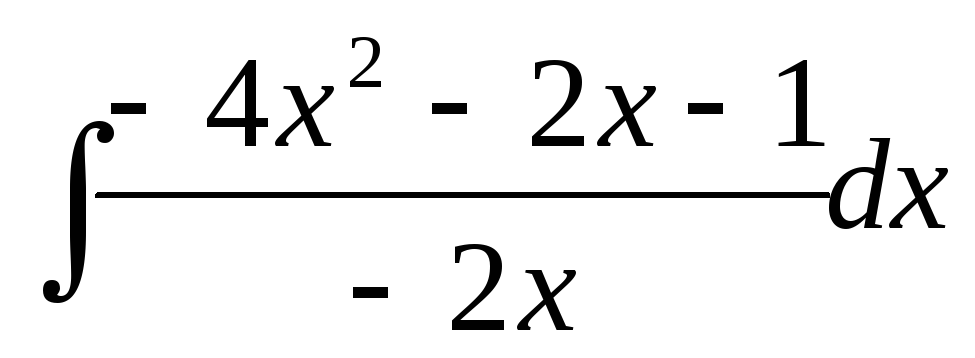

-
Вычислить неопределенный интеграл
 .
.

-
Вычислить неопределенный интеграл

-
Вычислить определенный интеграл

-
Вычислить определенный интеграл

-
Вычислить определенный интеграл
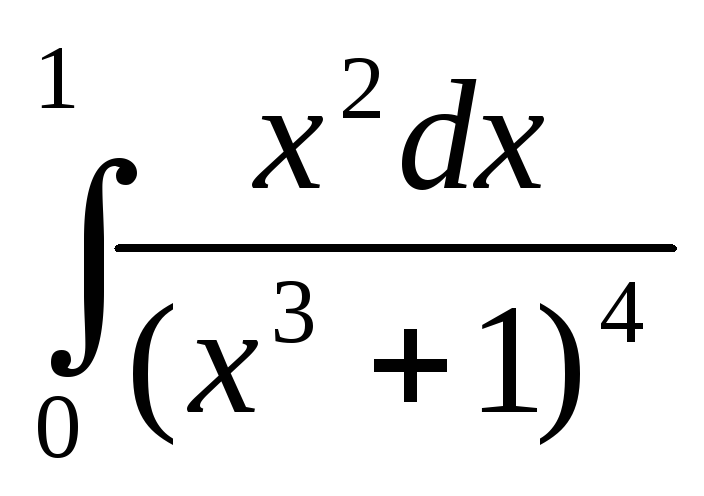
-
Решить дифференциальное уравнение


-
Решить задачу Коши:
 ,
,  .
.
Вариант № 6 Задание № 1
-
Найти пределы функции
 при различных значениях ɑ (не применяя
правила Лопиталя):
при различных значениях ɑ (не применяя
правила Лопиталя):
y =![]() ɑ
= 2; ɑ = 5; ɑ
.
ɑ
= 2; ɑ = 5; ɑ
.
-
Вычислить производную функций:
1).
![]() ;
;
2).
![]() .
.
-
Вычислить y' в точке x0 :
![]() ; x0
= 3.
; x0
= 3.
-
Найти экстремумы функции.
![]()
-
Найти наибольшее и наименьшее значение функции y на отрезке [ – 6, – 2]:

-
Вычислить
 ,
используя правило Лопиталя:
,
используя правило Лопиталя:
![]() ; ɑ
= – 1.
; ɑ
= – 1.
Задание № 2
-
Вычислить неопределенный интеграл


-
Вычислить неопределенный интеграл

-
Вычислить неопределенный интеграл

-
Вычислить определенный интеграл

-
Вычислить определенный интеграл

-
Вычислить определенный интеграл

-
Решить дифференциальное уравнение


-
Решить задачу Коши:
 ,
, 
Вариант № 7 Задание № 1
-
Найти пределы функции
 при различных значениях ɑ (не применяя
правила Лопиталя):
при различных значениях ɑ (не применяя
правила Лопиталя):
y =![]() ɑ
= 1; ɑ = – 4; ɑ
.
ɑ
= 1; ɑ = – 4; ɑ
.
-
Вычислить производную функций:
1).
![]() ;
;
2).
![]() .
.
-
Вычислить y' в точке x0 :
![]() ; x0
= 5.
; x0
= 5.
-
Найти экстремумы функции:
![]() .
.
-
Найти наибольшее и наименьшее значение функции y на отрезке [2, 9]:
![]()
-
Вычислить
 ,
используя правило Лопиталя:
,
используя правило Лопиталя:
![]() ; ɑ
= –3.
; ɑ
= –3.
Задание № 2
-
Вычислить неопределенный интеграл
 .
.

-
Вычислить неопределенный интеграл
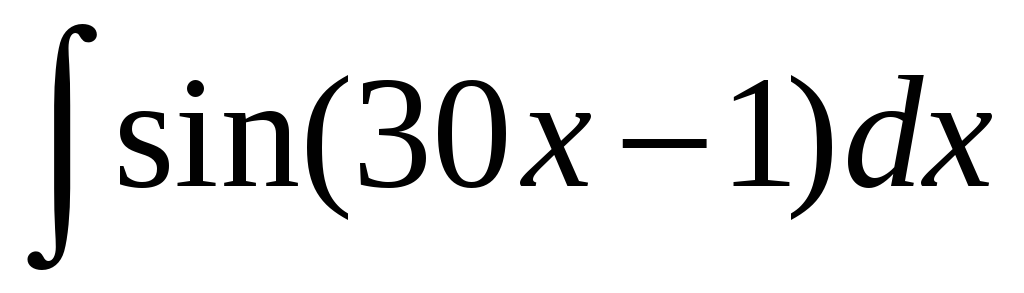 .
. -
Вычислить неопределенный интеграл
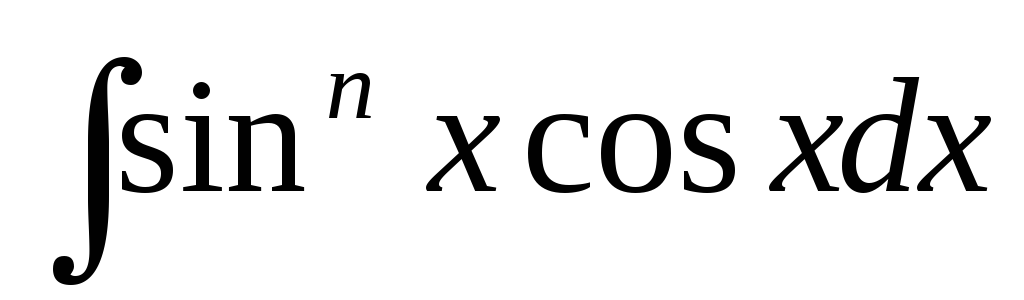 .
. -
Вычислить определенный интеграл
 .
. -
Вычислить определенный интеграл
 .
. -
Вычислить определенный интеграл
 .
. -
Решить дифференциальное уравнение

 .
. -
Решить задачу Коши:
 ,
,  .
.
Вариант № 8 Задание № 1
-
Найти пределы функции
 при различных значениях ɑ (не применяя
правила Лопиталя):
при различных значениях ɑ (не применяя
правила Лопиталя):
y =![]() ɑ
= 5; ɑ = – 5; ɑ
.
ɑ
= 5; ɑ = – 5; ɑ
.
-
Вычислить производную функций:
1).
![]() .
.
2).
![]()
-
Вычислить y' в точке x0 :
![]() ; x0
=3.
; x0
=3.
-
Найти экстремумы функции:
![]() .
.
-
Найти наибольшее и наименьшее значение функции y на отрезке [1, 8]:
![]() .
.
-
Вычислить
 ,
используя правило Лопиталя:
,
используя правило Лопиталя:
![]() ; ɑ
= 3.
; ɑ
= 3.
Задание № 2
-
Вычислить неопределенный интеграл
 .
.

-
Вычислить неопределенный интеграл
 .
. -
Вычислить неопределенный интеграл
 .
. -
Вычислить определенный интеграл
 .
. -
Вычислить определенный интеграл

-
Вычислить определенный интеграл

-
Решить дифференциальное уравнение


-
Решить задачу Коши:
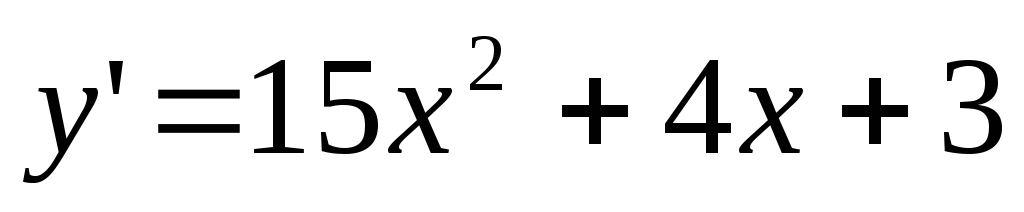 ,
,  .
.
