4.2. Пример выполнения задания

Найдем максимальный поток в сети, представленной на рис. 4.2. На рис. 4.3 предлагается графическая иллюстрация выполнения алгоритма. Считаем полезным сравнить описание выполняемых алгоритмом вычислительных итераций с их графическим представлением.

Рис. 4.2. Сеть для примера 4.2

Итерация 1. Положим остаточные пропускные способности всех ребер равными первоначальным пропускным способностям .

Шаг 1. Назначаем и помечаем узел 1 меткой . Полагаем .

Шаг 2. .

Шаг 3. , поскольку

.

Назначаем и помечаем узел 3 меткой . Полагаем и возвращаемся ко второму шагу алгоритма.

Шаг 2. .

Шаг 3. и . Помечаем узел 5 меткой . Получен сквозной путь. Переходим к пятому шагу алгоритма.

Шаг 5. Сквозной путь определяем по меткам, начиная с узла 5 и заканчивая узлом 1: . Таким образом, и . Вычисляем остаточные пропускные способности вдоль пути :

,

.

Итерация 2 .

Шаг 1. Назначаем и помечаем узел 1 меткой . Полагаем .

Шаг 2. .

Шаг 3. , назначаем и помечаем узел 2 меткой . Полагаем и возвращаемся ко второму шагу алгоритма.

Шаг 2. .

Шаг 3. и . Помечаем узел 3 меткой . Полагаем и возвращаемся к шагу 2.

Шаг 2. (отметим, что , поэтому узел 5 не включается в ).

Шаг 3. , назначаем и помечаем узел 4 меткой . Полагаем и возвращаемся к шагу 2.

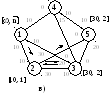
Рис. 4.3. Последовательное выполнение алгоритма нахождения максимального потока

Шаг 2. (поскольку узлы 1 и 3 уже помечены, они не включаются в ).

Шаг 3. и . Помечаем узе 5 меткой сквозной путь. Переходим к шагу 5.

Шаг 5. и . Вычисляем остаточные пропускные способности вдоль пути :

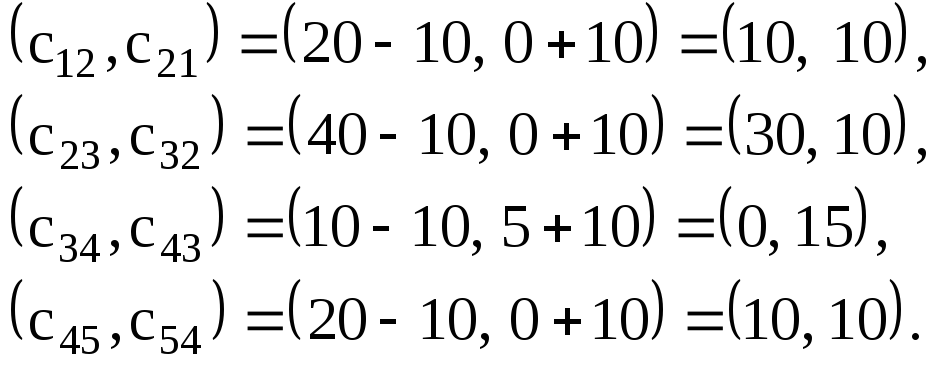
Итерация 3.

Шаг 1. Назначаем и помечаем узел 1 меткой . Полагаем .

Шаг 2. .

Шаг 3. , назначаем и помечаем узел 2 меткой . Полагаем и возвращаемся к шагу 2.

Шаг 2. .

Шаг 3. и . Помечаем узел 3 меткой . Полагаем и возвращаемся к шагу 2.

Шаг 2. (поскольку ). Переходим к шагу 4.

Шаг 4. Метка узла 3 показывает номер предшествующего узла . На этой итерации узел 3 в дальнейшем во внимание не принимается, его метку вычеркиваем. Полагаем и возвращаемся к шагу 2.

Шаг 2. (поскольку узел 3 удален из возможного сквозного пути).

Шаг 3. и . Помечаем узе 5 меткой сквозной путь. Переходим к шагу 5.

Шаг 5. и . Вычисляем остаточные пропускные способности вдоль пути :

Итерация 4. На этой итерации получен путь с .

Итерация 5. На этой итерации получен путь с .

Итерация 6. Новые сквозные пути невозможны, поскольку все ребра, исходящие из узла 1, имеют нулевые остаточные пропускные способности. Переходим к шагу 6 для определения решения.

Шаг 6. Максимальный объем потока в сети равен

единиц.

Значения потоков по различным ребрам вычисляются путем вычитания последних значений остаточных пропускных способностей (т.е. ) из первоначальных значений пропускных способностей . Результаты вычислений приведены в следующей таблице.

Ребро		Величина потока	Направления
	(20, 0) – (0, 20) = (20, -20)	20
	(30, 0) – (0, 30) = (30, -30)	30
	(10, 0) – (0, 10) = (10, -10)	10
	(40, 0) – (40, 0) = (0, 0)	0	–
	(30, 0) – (10, 20) = (20, -20)	20
	(10, 5) – (0, 15) = (10, -10)	10
	(20, 0) – (0, 20) = (20, -20)	20
	(20, 0) – (0, 20) = (20, -20)	20